We know that:

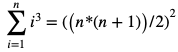
So, one of the best ways to create the array A of length n, is:

A[i]=i, where 1<=i<=n

Time Complexity: O(n), per test case.

Space Complexity: O(1), per test case.

#include<bits/stdc++.h>
using namespace std;
int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    int t;
    cin >> t;
    while(t--)
    {
        int n;
        cin >> n;
        for(int i=1;i<=n;++i)
        	cout << i << " ";
        cout << '\n';
    }
    return 0;
}

Bitwise-XOR of any number, X with 0 is equal to the number itself (X).

So, if we set the first element of the Array A as X, and the next K-1 elements as 0, then we will have the XOR of first sub-array of length K, equal to X, which is required.

XOR(A[0],...,A[K-1]) = X

Now, if we set A[K] as A[0], then we will have XOR(A[1],...,A[K]) = X

Similarly, if we set A[K+1] as A[1], then we will have XOR(A[2],...,A[K+1]) = X

And continuing so, we can observe that the general formula can be described as below:

A[i] = X, when i%K==0 and 0<=i<=N-1

A[i] = 0, when i%K!=0 and 0<=i<=N-1

Time Complexity: O(N), per test case.

Space Complexity: O(K), per test case.

#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    int t;
    cin >> t;
    while(t--)
    {
        ll n,k,_xor;
        cin >> n >> k >> _xor;
        vector<ll> ans(k,0);
        ans[0]=_xor;
        for(int i=0;i<n;++i)
        	cout << ans[i%k] << " ";
        cout << '\n';
    }
    return 0;
}

Let DP[i][j] denote the number of possible arrays, where i denotes the Last (Smallest) number in the Array, and j denotes the Size of the Array.

If the size of the array is 1, no matter whatever is the value of i, the following equation will always be true:

DP[i][1] = 1

Observe here that, the last (smallest) element of array of size j will always be less than or equal to last (smallest) element of array of size j-1.

Using this observation, we can generalise the DP table as follows:

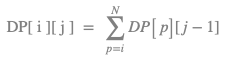where 1<=i<=N and 2<=j<=K.

The above equation takes O(N*N*K) time, for calculating the whole DP Table.

So, we will use Suffix Sums, to calculate the DP Table, using the above formula, in O(N*K) time.

Time Complexity: O(N*K)

Space Complexity: O(N*K)

#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
#define endl '\n'
int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    int n,k;
    cin >> n >> k;
    vector<vector<int>> dp(n+1,vector<int>(k+1));
    for(int i=1;i<=n;++i)
    {
    	dp[i][1]=1;
    }
    for(int i=n;i>=1;--i)
    {
        for(int j=2;j<=k;++j)
        {
            if(i==n)
                dp[i][j]=dp[i][j-1];
            else
                dp[i][j]=dp[i][j-1]+dp[i+1][j];
            dp[i][j]%=1000000007;
        }
    }
    ll ans=0;
    for(int i=1;i<=n;++i)
    {
        ans+=dp[i][k];
        ans%=1000000007;
    }  
    cout << ans << endl;
    return 0;
}

Let’s create the two-dimensional array dis[node][deg], which stores the ancestor of node at distance 2^deg.

If we fill this dis array, we can answer every query in lg(n) time, using Binary Lifting.

dis[node][0] = parent(node), for every node (except root)

dis[root][0] = -1, for root node.

So, now for deg from 1 to lg(n) and for each node,

dis[node][deg] = dis[dis[node][deg-1]][deg-1].

So, now, for each query node d, convert d into its binary representation and for every set bit in this binary representation, we replace node to dis[node][set-bit position from right], till the value of node doesn't become -1 or till all the set-bits of d are iterated.

Time Complexity: O((n+q)*(lg n))

Space Complexity: O(n*(lg n))

#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
#define endl '\n'
vector<vector<int>> adj;
vector<vector<int>> dis;
void bfs()
{
    queue<int> q;
    q.push(0);
    dis[0][0]=-1;
    while(!q.empty())
    {
        int temp=q.front();
        q.pop();
        for(int u:adj[temp])
        {
            if(u!=dis[temp][0])
            {
                dis[u][0]=temp;
                q.push(u);
            }
        }
    }
}
int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    int n,q;
    cin >> n >> q;
    adj = vector<vector<int>>(n);
    for(int i=0;i<n-1;++i)
    {
        int x,y;
        cin >> x >> y;
        --x;
        --y;
        adj[x].push_back(y);
        adj[y].push_back(x);
    }
    int logn = log2(n) + 1;
    dis = vector<vector<int>>(n,vector<int>(logn+1));
    bfs();
    for(int i=1; i<=logn; ++i)
    {
        for(int node=0; node<n; ++node)
        {
            if(dis[node][i-1]!=-1)
                dis[node][i]=dis[dis[node][i-1]][i-1];
            else
                dis[node][i]=-1;
        }
    }
    vector<int> po(logn+1);
    int temp=1;
    for(int i=0;i<=logn;++i)
    {
        po[i]=temp;
        temp=2*temp;
    }
    while(q--)
    {
        int node,d;
        cin >> node >> d;
        --node;
        for(int i=logn; i>=0; --i)
        {
            if(d>=po[i])
            {
                d-=po[i];
                node=dis[node][i];
            }
            if(node==-1)
                break;
        }
        if(node==-1)
            cout << -1 << endl;
        else
            cout << node+1 << endl;
    }
    return 0;
}

We will work using the "Binary (Bit) Representation" of all the variables.

Since, we need to find the minimum value of c, so, we will derive some conditions, for a particular bit position to be set (1) or reset (0) in the bit (binary) representation of c.

The conditions (For a particular bit position)
 are:

1. The bit position of a xor b is reset (0). (The bit position of a & b is same)
2. The bit position of d is reset (0).
3. The bit position of e is reset (0).

When all the above three conditions hold for a particular bit position, only then, that particular bit position of c will be set (1).

Hence, we derived the "Binary Representation" of required value of c, which will give the maximum value of the equation ((((a^b)|c)^d)|e).

So, just convert it into its Integer Representation, and that will be the required minimum value of c, for which the value of the equation ((((a^b)|c)^d)|e), will be maximum.

Time Complexity: O(1), per test case.

Space Complexity: O(1), per test case.

#pragma GCC optimize("O3")
#pragma GCC optimize("O1")
#pragma GCC optimize("O2")
#pragma GCC optimize("Os")
#pragma GCC optimize("Ofast")
#pragma GCC target("avx2")
#pragma GCC optimization("unroll-loops")
#include <bits/stdc++.h>
#define FAST ios_base::sync_with_stdio(false);
#define FO cout.tie(NULL);
#define FI cin.tie(NULL);
#define IN cin>>
#define OUT cout<<
#define loop(i,a,n) for(ll i=a; i<n; i++)
#define rloop(i,a,n) for(int i=a; i>=n; i--)
#define endl "\n";
#define pb push_back
#define mp make_pair
#define set_bits(a) __builtin_popcountll(a)
#define ll long long int
#define ld long double
#define vll vector<long long int>
#define pll pair<long long int, long long int>
#define mod 1000000007
#define M 998244353
using namespace std;
void vok()
{
    FAST
    FO
    FI
    #ifndef ONLINE_JUDGE
        freopen("input.txt","r",stdin);
        freopen("output.txt","w",stdout);
    #endif
}
int main()
{
    vok();
    int t;
    IN t;
    while(t--)
    {
        ll a,b,d,e;
        IN a>>b>>d>>e;
        ll axb=a^b;
        bitset<60> be(e), ans(0), bd(d), a_xor_b(axb);
        bitset<60> a_xor_b_or_c(0);
        loop(i,0,60)
        {
            if(!be[i] && !bd[i]) //Bit Position of 'e' and 'd' is Reset.
            {
                a_xor_b_or_c[i]=1; //We will want a_xor_b_or_c's Bit Position to be 1.
            } 
        }
        loop(i,0,60)
        {
            if(a_xor_b_or_c[i] && !a_xor_b[i])
            {
                ans[i]=1; //Set the c's bit position to 1
            }
        }
        ll c=ans.to_ulong();
        OUT c<<endl
    }
    return 0;
}

• Case-1: (n=0 or n=1)

You can directly find the nth term of the FX Sequence in O(1), using the given values of starting terms of the sequences, MFS and XS.

• Case-2: (n>=2)

The nth term of the MFS Sequence can be found using Matrix Exponentiation.

We have: MFS(x)= e*MFS(x-1) + f*(MFS(x-2)

In the form of Matrices, it can be written as:

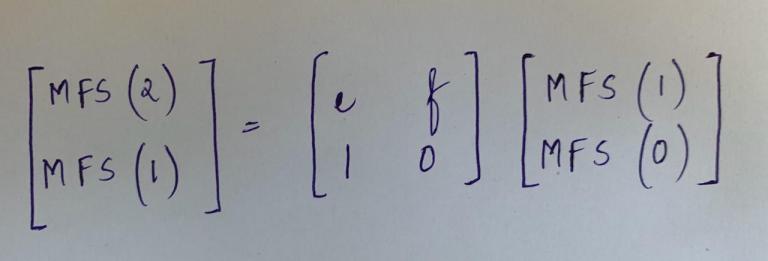
Hence, 



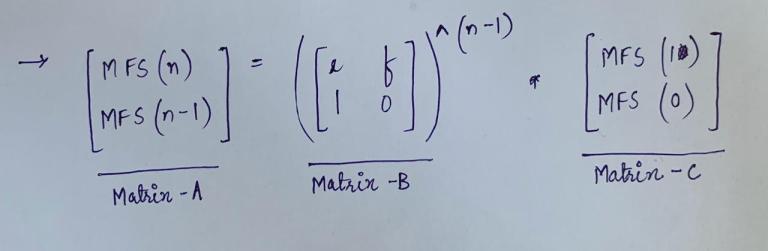
So, using Matrix Exponentiation, we will find the (n-1)th Power of the Matrix (which we call, Matrix-B), in O(lg(n-1)) time.

After that, we just have to multiply this Matrix-B with Matrix-C, to get Matrix-A.

At the end, the first term of Matrix-A (A[0][0]) will be the n'th (required) term of the MFS Sequence.

Writing the first 5-7 terms of the XS sequence, in terms of c and d, we get:

c, d, c^d, d^(c^d), d^(c^d)^(c^d), …



which is nothing but,

c, d, c^d, c, d, c^d, …

Hence, we can see that the sequence repeats itself, after every 3 terms.

Thus, the n'th term of this sequence can be found in O(1) time.

1. When n%3==0, then XS(n) = c
2. When n%3==1, then XS(n) = d
3. When n%3==2, then XS(n) = c^d

Now, we found the n'th terms of both the sequences, MFS and XS, so, now, we can find the n'th term of the FX Sequence in O(1) time.



Time Complexity: O(lg(n)), per test case.

Space Complexity: O(1), per test case.

#pragma GCC optimize("O3")
#pragma GCC optimize("O1")
#pragma GCC optimize("O2")
#pragma GCC optimize("Os")
#pragma GCC optimize("Ofast")
#pragma GCC target("avx2")
#pragma GCC optimization("unroll-loops")
#include <bits/stdc++.h>
#define FAST ios_base::sync_with_stdio(false);
#define FO cout.tie(NULL);
#define FI cin.tie(NULL);
#define IN cin>>
#define OUT cout<<
#define loop(i,a,n) for(ll i=a; i<n; i++)
#define rloop(i,a,n) for(int i=a; i>=n; i--)
#define endl "\n";
#define pb push_back
#define mp make_pair
#define set_bits(a) __builtin_popcountll(a)
#define ll long long int
#define ld long double
#define vll vector<long long int>
#define pll pair<long long int, long long int>
#define mod 1000000007
#define M 998244353
using namespace std;
void vok()
{
    FAST
    FO
    FI
    #ifndef ONLINE_JUDGE
        freopen("input.txt","r",stdin);
        freopen("output.txt","w",stdout);
    #endif
}
ll n,a,b,c,d,e,f;
void multiply(ll m1[2][2], ll m2[2][2]) 
{ 
    ll res[2][2]; 
    loop(i,0,2)
    { 
        loop(j,0,2)
        { 
            res[i][j]=0; 
            loop(k,0,2)
            {
                res[i][j]+=((m1[i][k]%M)*(m2[k][j]%M)); 
                res[i][j]%=M;
            }
        } 
    } 
    loop(i,0,2)
    {
        loop(j,0,2)
        {
            m1[i][j]=res[i][j];
        }
    }
} 
ll power(ll fib[2][2], ll n)
{
    if(n==1)
    {
        return (((b*fib[0][0])%M)+((a*fib[0][1])%M))%M;
    }
    ll mul[2][2]={{e,f},{1,0}};
    power(fib,n/2);
    multiply(fib,fib);
    if(n%2)
    {
        multiply(fib,mul);
    }
    return (((b*fib[0][0])%M)+((a*fib[0][1])%M))%M;
}
ll n_th(ll n)
{
    ll fib[2][2]={{e,f},{1,0}};
    return power(fib,n-1);
}
int main()
{
    vok();
    int t;
    IN t;
    while(t--)
    {
        IN n>>a>>b>>c>>d>>e>>f;
        a%=M;
        b%=M;
        e%=M;
        f%=M;
        if(n==0)
        {
            ll mfs=a;
            ll xs=c%M;
            ll fx=mfs*xs;
            fx%=M;
            fx+=mfs;
            fx%=M;
            fx-=xs;
            fx+=M;
            fx%=M;
            OUT fx<<endl
        }
        else if(n==1)
        {
            ll mfs=b;
            ll xs=d%M;
            ll fx=mfs*xs;
            fx%=M;
            fx+=mfs;
            fx%=M;
            fx-=xs;
            fx+=M;
            fx%=M;
            OUT fx<<endl
        }
        else
        {
            ll xs;
            if(n%3==0)
            {
                xs=c%M;
            }
            else if(n%3==1)
            {
                xs=d%M;
            }
            else
            {
                xs=(c^d)%M;
            }
            ll mfs=n_th(n); //Calculate n'th term of the MFS Seq.
            ll fx=mfs*xs;
            fx%=M;
            fx+=mfs;
            fx%=M;
            fx-=xs;
            fx+=M;
            fx%=M;
            OUT fx<<endl
        }
    }
    return 0;
}

This question is based on Markov Chains. So, for this question, we have to first find the Transition Probability Matrix, from the Given Matrix.

Let’s call this Transition Probability Matrix as Matrix-P, and the given matrix as Matrix-A, where:

P[i,j] = A[i][j] / Sum(Row-i)

Using Markov Chain’s Finite State Transition Formula, we get that, the probability of going from Time State-i to Time State-j in exactly k steps (state changes) can be defined as:

 P^k[i][j]

Since we have queries upto 10^5, and k is also upto 10^5. So, it is clear that the Brute-Force solution will give TLE.

So, basically, we will get the input of all the queries first, and then sort them in increasing order, with respect to the value of k.

While calculating the powers of the Matrix-P, we will save the answer for all the queries with k = Current Power of the Matrix.

At the end, we can print the saved answer (probability) for each query.

Time Complexity: O(max(k)*(n^3) + q)

Space Complexity: O(n^2)

Some links, to learn more about Markov Chains:

1. https://setosa.io/ev/markov-chains/
2. https://en.wikipedia.org/wiki/Markov_chain
3. https://towardsdatascience.com/introduction-to-markov-chains-50da3645a50d
4. https://brilliant.org/wiki/absorbing-markov-chains/
5. https://math.dartmouth.edu/archive/m20x06/public_html/Lecture14.pdf

#pragma GCC optimize("O3")
#pragma GCC optimize("O1")
#pragma GCC optimize("O2")
#pragma GCC optimize("Os")
#pragma GCC optimize("Ofast")
#pragma GCC target("avx2")
#pragma GCC optimization("unroll-loops")
#include <bits/stdc++.h>
#define FAST ios_base::sync_with_stdio(false);
#define FO cout.tie(NULL);
#define FI cin.tie(NULL);
#define IN cin>>
#define OUT cout<<
#define loop(i,a,n) for(ll i=a; i<n; i++)
#define rloop(i,a,n) for(int i=a; i>=n; i--)
#define endl "\n";
#define pb push_back
#define mp make_pair
#define set_bits(a) __builtin_popcountll(a)
#define ll long long int
#define ld long double
#define vll vector<long long int>
#define pll pair<long long int, long long int>
#define mod 1000000007
#define M 998244353
using namespace std;
void vok()
{
    FAST
    FO
    FI
    #ifndef ONLINE_JUDGE
        freopen("input.txt","r",stdin);
        freopen("output.txt","w",stdout);
    #endif
}
bool comp(const array<int,4> &a, const array<int,4> &b)
{
    return a[0]<b[0];
}
int main()
{
    vok();
    int n;
    IN n;
    OUT fixed<<setprecision(8);
    ld a[n][n];
    ld rowsum[n];
    memset(rowsum,0.0,sizeof(rowsum));
    loop(i,0,n)
    {
        loop(j,0,n)
        {
            IN a[i][j];
            rowsum[i]+=a[i][j];
        }
    }
    ld probability_mat[n][n], tprobability_mat[n][n];
    loop(i,0,n)
    {
        loop(j,0,n)
        {
            probability_mat[i][j]=a[i][j]/rowsum[i];
            tprobability_mat[i][j]=a[i][j]/rowsum[i];
        }
    }
    int q;
    IN q;
    vector<array<int,4>> queries(q);
    //queries[i][0] -> k
    //queries[i][1] -> x
    //queries[i][2] -> y
    //queries[i][3] -> index of the query (i)
    int max_power_required=0;
    loop(i,0,q)
    {
        IN queries[i][1]>>queries[i][2]>>queries[i][0];
        queries[i][1]--, queries[i][2]--;
        queries[i][3]=i;
        max_power_required=max(max_power_required,queries[i][0]);
    }
    sort(queries.begin(),queries.end(),comp);
    int curr_power=1;
    int curr_ind=0;
    ld ans[q];
    while(curr_power<=max_power_required && curr_ind<q)
    {
        //Save the answer for queries, having k=curr_power
        while(curr_ind<q && curr_power==queries[curr_ind][0])
        {
            ans[queries[curr_ind][3]]=probability_mat[queries[curr_ind][1]][queries[curr_ind][2]];
            curr_ind++;
        }

        //Calculate P^(curr_power + 1)
        ld temp[n][n];
        loop(i,0,n)
        {
            loop(j,0,n)
            {
                temp[i][j]=0.0;
                loop(k,0,n)
                {
                    temp[i][j]+=(probability_mat[i][k]*tprobability_mat[k][j]);
                }
            }
        }
        loop(i,0,n)
        {
            loop(j,0,n)
            {
                probability_mat[i][j]=temp[i][j];
            }
        }
        curr_power++;
    }

    //Answer all the queries
    loop(i,0,q)
    {
        OUT ans[i]<<endl
    }
    return 0;
}