Lien's blog

calculate 1+a^1+a^2+...+a^d mod m
By Lien, 11 years ago, In English

Hi! I'm now thinking about calculate geometric sum: 1+a+a^2+..+a^n mod m where a,m,n are 64-bit integer. I transform 1+a+a^2+...+a^n mod m=(a^(n+1)-1)/(a-1) mod m but a new problem appear: when gcd(a-1,m)>1 it seem impossible to find t such that t*(a-1) mod m=1. Any hint for this problem?

  • Vote: I like it
  • +13
  • Vote: I do not like it

»
11 years ago, # |
  Vote: I like it +21 Vote: I do not like it

You can use the same idea as in binary exponentiation. Just calculate this sum together with an + 1 and you can easily write down formulas for transitions.

→ Reply
»
11 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

S = ( 1+a+a^2+...+a^(sqrt(n)-1) )%m; // sqrt(n) max that sqrt(n)*sqrt(n)<=n

t= (a^sqrt(n))%m;

ans=1;

for(int i=0; i<sqrt(n); i++) ans = ((ans*t)+S)%m;

for(int i=0; i<(n- sqrt(n)*sqrt(n); i++) ((ans*a)+1)%m;

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it -8 Vote: I do not like it

    You looked like liverpool FC fans!!!I am Kopite too....It's so wanderful

    → Reply
»
11 years ago, # |
  Vote: I like it +51 Vote: I do not like it

It can also be done using matrix exponentiation: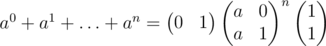

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it -17 Vote: I do not like it

    This breaks a butterfly upon a wheel.

    → Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Can you give some links to editorials or some books which can help to improve skill of seeing this kind of "matrix patterns"? Or this is just your own experience?

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it +13 Vote: I do not like it

      I use the following: imagine you have some loop which alters several variables in linear way, for example:

      int a = 1, b = 2, c = 3;
for (int i = 0; i < n; i++) {
  int a1 = a + b - c;
  int b1 = 2 * a + c;
  int c1 = b + 4 * c;
  a = a1;
  b = 1;
  c = c1;
}

      Then let's imagine that we have one row vector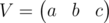 instead of three variables. Each iteration of loop alters this vector in some linear way, thus, we can represent one iteration as a matrix: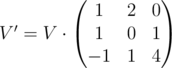

      After than we can easily simulate any amount of loop's iterations in logarithmic time.

      → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I use almost the same idea as yeputons: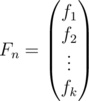
      We have vector
      Lets construct such matrix A that Fn + 1 = AFn.
      Then Fn = AnF0.

      In this case, f1 = an, f2 = S(n):

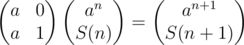
      In order to better understand this, it is useful to construct such matrices for these sums: , , , , , .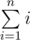
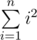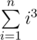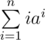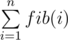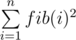      fib(i) — i-th Fibonacci number.

      → Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it -14 Vote: I do not like it

    seems like we can generalize this formula: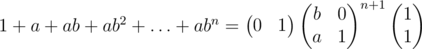

    → Reply
»
11 years ago, # |
  Vote: I like it -12 Vote: I do not like it

Looks like you have a problem with modulus arithmetics and division. As far as it is simple to do addition and multiplication in modulus arithmetics, it is not obvious how to do division. Have a look at first comment to this post It says that is modulus is a prime number and you want to calculate (a / x) MOD m you can calculate inverse element inv = x m-2 and then multiply a * inv

→ Reply
»
11 years ago, # |
  Vote: I like it +5 Vote: I do not like it

It's possible to perform the calculation of an + 1 - 1 modulo m * (a - 1) and then perform the division by a - 1. The proof of correctness goes into the Chinese Remainder Theorem.

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    m*(a-1) may exceed the limitation of 64-bit integer

    → Reply