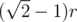итак, есть задача: дан двумерный массив размерами до 5000, требуется отвечать на запросы вида (i, j, r), ответом будет сумма/минимум/максимум элементов массива с индексами x, y, таких что (x - i)2 + (y - j)2 ≤ r2. Интересуют идеи как онлайн, так и оффлайн решения задачи. Решения за O(r) на запрос не предлагать, ибо слишком скучно.
зы. Источника задачи нет, т.к. возникла у меня в голове:-)











Сразу вспоминается задача Е с Гран-При Украины. Там, правда, на запросы наложено дополнительное ограничение вложенности.
Оффтопик, но может помочь доработать решение задачи, на которую Вы сослались, до решения задачи в общем виде: а как решается задача о подсчете количества точек пересечения N окружностей лучше, чем за O(N2)?
Построим квадрат (i;j-r), (i-r;j), (i;j+r), (i+r;j). Он повернут на 45 градусов, и, думаю, искать, например, сумму в нем можно. Теперь нужно взять сумму на полосках, параллельных сторонам этого квадрата. Понятно, что для всех 4 сторон выходит симметрично, поэтому только одну рассмотрим. Из того, что я порисовал, выходит, что полосок вроде не более двух, и их длины — (r-2) и (r-1), причем если провести перпендикуляр из центра квадрата к стороне, то он будет осью симметрии этих полосок.
Я думаю, полосок будет примерно