Здравствуйте. Мне пришла в голову одна задача, которую я не умею решать;) Даны N<=10^5 целых чисел от 1 до 10^9, и дано Q запросов, каждый из которых представляет целое число X, 1<=X<=10^9. Для каждого запроса нужно вывести количество чисел из списка, которые нацело делятся на X. Интересно, существует ли решение (онлайн/оффлайн) быстрее, чем за O(N) за запрос?.. Заранее спасибо;)
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
25:36:29
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
25:36:29
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 15:58:31 (g1).
Десктопная версия, переключиться на мобильную.
При поддержке
Совсем недавно была такая задача, но там числа до 10^5.
Ага, значит, идея не нова;) А то, что всегда L=0 и R=N-1, задачу никак не упрощает?..
Пришло в голову такое: у каждого числа не очень много делителей, для больших чисел не больше кубического корня. Загенерим для нашего списка все делители и отметим (например в мапе или хеш таблице) сколько раз каждый из них встретился. Потом в онлайне можно отвечать быстро на запросы.
Только хотел написать про то же. Еще добавлю, что факторизовать числа для нахождения их делителей лучше всего с помощью ρ-алгоритма Полларда.
Спасибо большое, похоже на правду;) Единственное — не может ли в сумме делителей оказаться слишком много (скажем, 2*10^8) так, что они не влезут в память?
vlad107 ниже предложил учитывать только те делители, которые есть в запросах. А на самом деле, делителей максимум O(sqrt(MAXVAL) + N) — у каждого числа может быть не более одного делителя больше корня, а всего различных делителей меньше корня — понятно, сколько.
UPD. Насчет любых делителей больше корня я все-таки наврал. Это утверждение верно только для простых делителей.
А как в онлайне быстро отвечать на запросы?
Так мы же для каждого числа уже нашли все его делители и запихали их в map.
А, дошло, извините :)
10^8 чисел не очень приятно хешировать, тогда уже логичнее вначале захешировать все запросы, а потом учитывать только те делители, которые есть в запросах.
Ага, красиво;) Получается, искать придется все равно все делители, но хешируются только нужные? Да, и кто-нибудь знает константу ρ-алгоритма Полларда?
Я тестировал его на полупростых числах порядка 10^18 с умножением по модулю за логарифм и проверкой на простоту с помощью BigInteger.isProbablePrime(100). Отрабатывало меньше, чем за секунду на очень старом железе (Pentium 4 640, 3.2ГГц). Учитывая асимптотику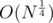
, можете делать выводы.
Однако... Даже если это старое железо делает всего миллион операций за "меньше, чем за секунду", получается константа 30;) Такое впечатление, что в моем случае быстрее будет идти по простым числам до корня...
Я только что сравнил Полларда с перебором делителей на худших тестах против того и другого, т.е. полупростых числах порядка 10^9 с примерно равными делителями, при установке 1024 итераций до сброса начального значения Поллард все-таки работает чуть быстрее. А в целом — время работы все-таки слишком большое, поэтому стоит снижать ограничения до 10^7, чтобы заходило решето Эратосфена.
Вот мой код.
Хм, странно... Казалось бы — до корня из миллиарда 3-4 тысячи простых чисел, итого 300-400М взятий по модулю, секунд за 5 должно бы проходить... А если уменьшить ограничения до 10^8, простых чисел будет еще в 3 раза меньше, так что, наверное, это уже будет выгоднее, чем Поллард.
В-общем, задача потеряла всю свою идейность и свелась к простому упихиванию факторизации 10^5 чисел :).
Увы;) На самом деле, изначально я придумал более сложную задачу — дано N различных чисел, нужно найти такое минимальное число X, что не более k чисел дают одинаковый остаток при делении на X. Но тут я уже не знаю, решается ли она даже за квадрат:(
В действительности достаточно пустить какое-нибудь решето до скажем N=10^5, затем перебрать все простые до K=10^9/N которых очень немного, и затем если число поделится найти остальные числа в разложении на простые. Т.е. Для Q=10^5 задача спокойно решается за пару секунд.
Вроде бы еще можно сохранить все различные числа из запросов, сжать их, а потом сделать sqrt-декомпозицию, хранить cnt[num][i] — количество чисел из блока num, делящихся на i-ый делитель из списка запросов. Если использовать хэш таблицу, то получается O(NsqrtN) на предпосчет и O(sqrtN) на запрос.
Извините, не могли бы вы поподробнее объяснить, как делается предпросчет за O(NsqrtN)? У вас N чисел и Q запросов, для каждой пары вы делаете проверку для обновления cnt. Итого O(NQ). Извините, если неправильно понял вашу идею.
Просто иду по массиву слева направо, и для текущего числа смотрю все его делители, если какой — то делитель встречался в запросах, то смотрю какой он сжатый и обновляю cnt. Псевдокод :
Ярые минусующие не любят корневую?
А причем тут корневая? У вас это работает за n×sqrt (max_a)×map. У вас, кажется, наблюдается непонимание поставленной задачи.
Извините, неправильно понял условие.