349A - Очередь в кино
В задаче требовалось выяснить, может ли кассир выдать сдачу всем посетителям кинотеатра, если билет стоит 25 рублей, у посетителей купюры номиналом 25, 50 и 100 и в кассе изначально нет денег.
Рассмотрим 3 различных случая.
- Если у посетителя 25 рублей, то сдачу ему давать не нужно.
- Если у посетителя 50 рублей, то мы должны дать ему 25 рублей сдачи.
- Если у посетителя 100 рублей, то мы должны дать ему 75 рублей сдачи. Это можно сделать двумя способами. 75=25+50 и 75=25+25+25. Заметим, что всегда выгодно попробовать сначала первый способ, а потом второй. Это верно потому, что купюры номиналом 25 рублей могут быть использован как для выдачи сдачи на 50 рублей, так и на 100 рублей, а сами купюры номиналом 50 рублей могут использоваться только для выдачи сдачи на 100 рублей.
Таким образом решение – поддерживать количество купюр номиналом 25 и 50 рублей и при выдаче сдачи на 100 рублей действовать жадно – сначала пробовать выдать 25+50 рублей, а иначе 25+25+25 рублей.
349B - Раскраска забора
В задаче требовалось выяснить наибольшее число, которое можно написать, используя заданное количество краски, если на каждую цифру тратится также известное количество краски.
Поскольку чем длиннее число, тем оно больше, нам выгодно написать число наибольшей длины. Для этого выберем цифру, на которую нужно меньше всего краски. Пусть количество краски для написания этой цифры d равно x, а всего у нас есть v литров краски. Тогда мы можем написать число длины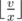 
.
Таким образом мы выяснили длину числа, пусть она равна len. Запишем промежуточный результат – строку длины len, состоящую из цифр d. У нас в запасе еще осталось v–len·x краски. Чтобы улучшить ответ, будем идти от начала числа и пробовать заменить каждую цифру на максимально возможную. Это верно потому, что числа одинаковой длины сравниваются сначала по старшим разрядам. Среди цифр больше текущей выбираем максимальную среди тех, на которую хватает краски, и обновляем текущее количество краски и ответ.
Если ответ длины 0, то нужно вывести -1.
348A - Мафия
В задаче требовалось определить, сколько игр нужно сыграть, чтобы все игроки остались довольны и сыграли как минимум столько игр, сколько они хотят.
Пусть ответ – это x игр. Заметим, что max(a1, a2, …, an) ≤ x. Тогда i-ый игрок может в x–ai играх быть ведущим. Если просуммировать по всем игрокам, то получим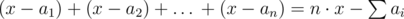 
— это количество игр, в которых игроки согласны быть ведущими. Это число должно быть не меньше x — нашего ответа.
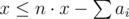
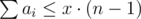
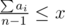
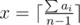
Также следует не забыть требование, что max(a1, a2, …, an) ≤ x.
348B - Яблоня
В задаче требовалось выяснить, какое минимальное количество яблок нужно удалить, чтобы сделать дерево сбалансированным.
Заметим, что если мы знаем значение в корне, то знаем значения во всех остальных вершинах. Значение в листе равняется значению в корне, поделенному на произведение степеней вершин на пути от корня до листа.
Для каждой вершины посчитаем величину di — какое минимальное число (не ноль) в ней должно быть записано, чтобы дерево по-прежнему могло быть сбалансированным. Для листьев di = 1, для остальных вершин di равен k·lcm(dj1, dj2, ..., djk), где j1, j2, ..., jk — сыновья вершины i. Также посчитаем величину si — сумму в поддереве вершины i. Все это можно сделать за один обход в глубину из корня дерева.
Вторым обходом в глубину мы можем посчитать для каждой вершины максимальное число, которое мы в нее можем записать, так чтобы удовлетворить ограничениям. А именно, пусть дана вершина i и k ее сыновей j1, j2, ..., jk. Тогда если m = min(sj1, sj2, ..., sjk), а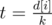 
— минимальное число, которое мы можем записать в сыновей вершины i, нам выгодно записать в сыновей вершины i числа 
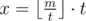. Остатки, а именно 
, добавим к ответу.
348C - Суммы подмножеств
В этой задаче на структуры данных требовалось использовать корневую эвристику или, по-другому, sqrt-декомпозицию.
Первый шаг решения состоял в том, чтобы разделить множества на легкие и тяжелые. Легкими назовем множества, которые содержат меньше 
элементов, а тяжелыми все остальные.
Ключевое наблюдение. В любом легком множестве меньше элементов, а количество тяжелых множеств также не превосходит , так как есть ограничение на сумму размеров множеств.
Чтобы эффективно отвечать на запросы, для каждого множества (как легкого, так и тяжелого) посчитаем размеры его пересечения со всеми тяжелыми множествами. Это можно сделать за время и память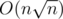 
. Для каждого тяжелого множества создадим булевский массив размера O(n), в i-ой ячейке которого будем хранить, сколько элементов i в этом множестве. Затем для каждого элемента и каждого тяжелого множества будем за O(1) проверять, содержится ли элемент в тяжелом множестве.
Теперь рассмотрим 4 возможных запроса:
Добавление к легкому множеству. Пройдем по всем числам множества и к каждому добавим нужное значение. Дальше пройдем по всем тяжелым множествам и к каждому добавим (размер пересечения * значение в запросе). Время работы
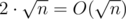.Добавление к тяжелому множеству. Просто увеличим счетчик для данного тяжелого множества на значение в запросе. Время работы O(1).
Ответ на запрос для легкого множества. Проходим по всем числам, добавляем значения к ответу. Затем проходим по всем тяжелым множествам и добавляем к ответу (добавление для данного тяжелого множества * размер пересечения со множеством в запросе). Время работы
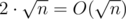.Ответ на запрос для тяжелого множества. Берем уже посчитанный ответ, затем проходим по тяжелым множествам и добавляем (добавление для данного тяжелого множества * размер пересечения со множеством в запросе). Время работы
.
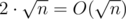Итого, если у нас O(n) запросов, то суммарное время работы .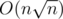
348D - Черепашки
В задаче требовалось найти количество пар непересекающихся путей из левого верхнего в правый нижний угол таблицы. Для этого можно воспользоваться следующей леммой. Спасибо rng_58 за ссылку. А именно, если переформулировать применительно к нашему случаю, то лемма утверждает, что если есть множества начальных A = {a1, a2} и конечных B = {b1, b2} точек, то ответ можно посчитать, как следующий определитель:
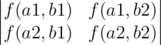
Наконец, заметим, что для того, чтобы свести исходную задачу к этой, нам нужно сделать пути, которые не имеют совсем совпадающих точек — в исходной задаче разрешаются пересечения в первой и последней точках пути. Для этого в качестве множеств A и B мы можем взять точки A = {(0, 1), (1, 0)} и B = {(n - 2, m - 1), (n - 1, m - 2)}
348E - Пилигримы
Давайте сначала построим простое решение этой задачи, а затем попробуем решить ее эффективно, учитывая данные ограничения.
Для каждой вершины найдем список наиболее удаленных вершин. Найдем вершины на пересечении путей от текущей вершины до каждой вершины из списка, в которых нет монастырей. Если мы удалим любую из этих вершин, то каждая вершина из списка будет недостижима из текущего монастыря. У каждой вершины из этого пересечения увеличим счетчик на единицу. Тогда ответ на задачу – максимум из счетчиков для всех вершин и количество таких максимумов.
Теперь решим задачу более эффективно, но используя ту же идею. Подвесим дерево за корень. Будем для каждой вершины искать список наиболее удаленных вершин только в ее поддереве. При обходе дерева в глубину из каждой вершины возвращаем наибольшую глубину в поддереве и номер вершины, на которой он достигается. Среди всех сыновей вершины выберем максимум из глубин. Если максимум достигается один раз, то вернем из текущей вершины тот же ответ, что был возвращен из сына. Если максимум достигается более одного раза, то вернем из текущей вершины номер текущей вершины. По сути, таким образом мы находим LCA всех наиболее удаленных от текущей вершины вершин. Перед выходом из вершины прибавляем единицу на отрезке от текущей вершины до найденного LCA. Это можно сделать, если хранить эйлеров обход графа и использовать дерево отрезков для прибавления на отрезке.
Наконец, последний этап решения задачи – решить ее для случая, когда наиболее удаленная вершина или их список находятся необязательно в поддереве текущей вершины. Для решения этой подзадачи используем ту же идею, которая используется при нахождении максимального по длине пути в дереве. Для каждой вершины будем хранить 3 максимума – 3 наиболее удаленные вершины в ее поддереве. Когда мы спускаемся в какое-то поддерево, то передаем заодно и 2 оставшихся максимума. Таким образом, находясь в любой вершине, мы можем решить, существует ли путь не в поддереве (то есть уходящий наверх) такой же или большей длины. Если в поддереве и вне его пути одинаковой длины, то это означает, что для пилигрима из текущего монастыря всегда найдется хотя бы один путь, какой бы город не удалили. Если одна из величин больше, то мы выбираем нужный отрезок в эйлеровом обходе дерева и увеличиваем на нем значение на единицу. Случай, когда есть несколько путей (то есть хотя бы 2) вне поддерева одинаковой максимальной длины, обрабатывается аналогично такому же случаю в поддереве.
Поскольку дерево отрезков может отвечать на запрос за O(logN) времени, а задачу LCA можно эффективно решить методом двоичного подъема за то же время, то затраты времени и памяти равны O(NlogN).
Таки, дождались ...
Спасибо ;)
Забавно твой комментарий эволюционировал)))
Благодарю за разбор.
Первые 40 минут решал В без дополнительного условия "во внутренних вершинах яблок нету". Оно хоть как-то решается? Или тотальный гроб?
Вроде можно свести к тому, что во внутренней вершине по прежнему ничего нету, создаем фиктивный лист, который подвешиваем за текущую внутреннюю вершину, и кидаем туда столько яблок, сколько было во внутренней вершине. UPD. Это бред.
Если я правильно понял идею, то таким образом мы получим дополнительное ограничение, которое отсутствовало в оригинальной задаче.
Например, если у вершины собственный вес 5, и есть сыновья 5 и 5, то простое создание дополнительного листа с перебросом туда 5 из внутренней вершины приведет к тому, что в этом поддереве будут возможными только суммы, кратные 3 — у нас пустая внутренняя вершина и, с учетом фиктивной вершины, 3 листа. И эти 3 листа надо балансировать, как в задаче с контеста. Хотя на самом деле в этом поддереве можно получить любую сумму от 0 до 15, пользуясь идеей "убираем 1 с внутренней вершины — прибавляем 1 к внутренней и убираем по 1 из листьев — убираем 1 с внутренней...".
Upd. Вот и я о том же, не работает)
Мда, я заметил наличие такого условия только сейчас, прочитав этот комментарий.
Как в DIV1 A доказать достаточность приведенных неравенств?
Построим конфигурацию игр по разбору. Пусть минимальная конфигурация такая, что количество игр y, y = x + d; при этом y — 1 недостаточное количество игр. Проверим это. Необходимые (перечисленные в разборе) неравенства выполняются для y = x + d, доказательство тривиально. Кроме того, для каждого i: (y — d — ai) ≥ 0. Так как y = x + d; (x — ai) ≥ 0, то справедливо: (y — ai) ≥ d, значит каждый сыграет на d игр больше чем нужно для минимума. Возникает противоречие, что и требовалось доказать.
Неясно, сначала идет неравенство (y — d — ai) ≥ 0, потом оно же переписанное в виде (y — ai) ≥ d и откуда-то возникает противоречие. При этом в доказательстве не используется неравенство x>=(a1 + ... + aN)/(n-1).
Пусть существуют РАЗЛИЧНЫЕ x и y для которых выполняются неравенства из разбора. При этом x из разбора по построению, а y — ответ, при этом y — x = d. Из построения (x — ai) >= 0. Тогда (y — d — ai) >= 0, (y — ai) >= d, при этом d строго больше нуля. Значит каждый сыграл как минимум (ai + d), то есть на d больше, чем хотел. Значит общее количество игр можно уменьшить. А противоречие возникает потому, что в самом начале доказательства я предположил, что количество игр "y" — минимально.
Update: понял о чем ты. Говоря по построению, я к раз и имею в виду минимальный Х соответствующий этому условию. А в условии (x — ai) >= 0 вместо проверки N условий, можно х сравнить с максимум из ai.
Я разобрался почему такое x подходит, правда используя чуть другие размышления.
P.S. На контесте зашел бинарный поиск по x=)
Из того, что (y — ai) >= d не следует, что каждый сыграл на d больше
Very nice idea for problem D. :) It's actually possible to solve problem E in O(n) time. LCA is not necessary, the "counting" process can be done by two dfs, first count the occurences of nodes in the "going up" part of paths, then count the occurences of nodes in the "going down" parts. You may see my solution for detail..
There's actually no need to use binary search in problem C, when finding intersections of sets. A brute-force implementation consumes only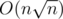
time.
I still don't get how it's done. There are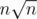
intersections to calculate, and each one takes n time..
For each element of each set see if it's contained in each big set (storing big sets in boolean arrays). There are N elements in total and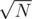
big sets, so it's 
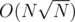time and space.
Ah, that's a nice way to analyze it. And if we use binary search instead of boolean array, it'll be n*sqrtn*logn. But then I don't get the n*sqrtn "brute force" approach.
I guess huzecong meant boolean arrays for big sets.
Sorry for not being clear, but a boolean array was what I meant... I thought that compared to the binary search approach this one seems pretty "brute-force"...
In the editorial we defined heavy sets to be those which contained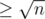
elements. Denoting 
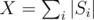, we have atmost 
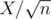heavy sets. If we go through each element of each set (X of those) and check if its contained in every heavy set (
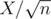of those), we have a complexity of 
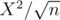which is out of limits. Am I missing anything?
According to problem statement, It is guaranteed that the sum of sizes of all sets Sk doesn't exceed 10^5. Naive solution works in (10^5)*(10^5)/sqrt(10^5), it is just few hundred millions of operations.
X ≤ 105, but with small n (like 4),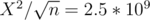
which is TLE? In the editorial is X = n ?
If you'll take heavy_size>=sqrt(X) — it will be ok, right? :)
I am not sure, but it looks like you are right, taking heavy_size>=sqrt(n) is bad idea.
But it will pass system tests) It do not proves that this solution is OK, it just shows us that tests are very weak. Take a look at 7288633, TsunamiNoLetGo has array for heavy sets of size 320 only, and heavy_size>=sqrt(n). It is easy to constuct testcase with 100000 heavy sets — just take n=1, m=100000, and all sets of size 1. But this solution passed, therefore i guess that such cases are missed in testdata.
Yes thats exactly what I meant. Setting heavy_size >= sqrt(X) is okay with me. SealView also told me that in the messages. He advises to set it to a constant (like 300). Thanks for looking into my problem. :D
in problem Apple trees can somebody explain the idea of finding intersections of sets using binary search
I think, you're talking about "Subset sums" problem.
Sort all lists. Iterate over one set and check whether element from this set is in another set. You can do it using binary_search() function from STL.
no apple trees 348B
There is no binary search and no sets in 348B.
I get a memory limit on problem Apple Tree. here is my submission : http://mirror.codeforces.com/contest/348/submission/4630566 Anybody knows why ?
The leaf of the Apple Tree can be 0. So lcm can be zero.
Can someone explain 348A — Mafia with more details, please? :|
Let's say you're going to play x games. If someone wanted to play more than x games, he wouldn't be able to do so, so he would be unhappy. Therefore, if everyone is happy, x ≥ ai must hold for each i, so
Let $b_i$ be number of games, where i-th player is supervisor and let ci be number of games, where he plays. In each game i-th player is playing, XOR supervising, so ci + bi = x. Also, he wants to play at least ai games, so ai ≤ ci, thus bi ≤ ci + bi - ai, so bi ≤ x - ai.
Each game is supervised by one player, so x = b1 + b2 + ... + bn. Giving it all together:
Now we have two lower bounds for $x$ . Smallest x satisfying both of them is
This number of games is enough, because if first $x - a_1$ games are supervised by first player, next x - a2 games are supervised by second player etc., until the x-th game, then everyone plays enough games and each game is supervised by someone.
In 348A-Mafia, How does this condition ensures that the value of 'x' found is minimum?
We simple do the binary search. Because of the principle of the binary search. We wouldn't be able to decrease x lower that lower bound in binary search(we checked the lower bound and found it impossible to fulfill the conditions by making only "lower bound" number games), similar for upper bound.
read discrete binary search from topcoder...you will understand
can some one explain following line from apple tree editorial. Line : The value in the leaf is equal to the value in the root divided to the product of the powers of all vertices on the path between root and leaf. how this come ?
value in a node = weight of a node.
power of a node = number of children of a node.
Let the value in the parent be X and power of it be K. Then value in each of its children will be X/K, as values of each children needs to be equal. Example:
A is the root and D is a leaf.
A (weight:X, power:3) --> B (weight:X/3, power:2) --> C (weight:X/(3*2), power:3) --> D (weight:X/(3*2*3)).
In Div. 1 Problem B, I didn't understand the idea behind d[i]. Why are we taking the lcm of all the children of the i'th vertex? What is the logic behind the solution. Could someone please help me out and elaborate?
Can anyone provide a more detailed solution for div1 B ??
Can someone provide a more detailed explanation for Div1 B ??
I don't know why does my solution for Div1B gets TLE... Can somebody help and take a look at it? Thanks in advance.
http://mirror.codeforces.com/contest/348/submission/19399532
Actually , We can solve Problem 348A-Mafia in a simpler way. let S = Σ a(i) for all i , c(i) = number of rounds played by the ith person so far , S2 = Σ c(i) for all i.
Then S2 is the Summation of the number of rounds played by each person so far. Actually , we need the number of Rounds X Which will make S2 >= S holds.
You Can Notice that after X Rounds , S2 Will be Equal to X*N — X , Were N is the number of People. Because simply , After each Round S2 will be incremented by the number of People -1 because all of them will play except one will be the supervisor.
So we just need to Search using Binary Search on the value X which will make X*N — X >= S holds .
NOTE : X should be >= max (a(i)).
Here is the link for my code.
20368610
Shouldn't we also need for all i (c[i]>=a[i]) after playing X rounds, & how does the condition S2>=S guarantees that
Problem B (div 2) has a tag of DP. how we can implement dp on this problem?
This may help.
thankyou hmrockstar your solution was great!!
DIV 2 B has dp tag, but it's a greedy problem :/
Div1 B, when we are calculating d[i] we are not considering the children of other nodes of the same level ?? for example, if root has 2 children and one of them has 3 children and another one has 2 children then we need to have the lcm of both 3 and 2 which is 6. please help !!
Anudeep's Submission of Problem Div1 C https://mirror.codeforces.com/contest/348/submission/4596270
Close to editorial!!!
DP approach for Div2 problem B
We can use the DP solution below. The approach is simple known as reconstructing the solution where we keep storing the optimal path in terms of parent of the state and then when we want to print we backtrack on the parent array. https://mirror.codeforces.com/contest/349/submission/107398509
Great code man. Really loved the code and idea behind it. Have you done similar problems before or is this the only problem you have ever encountered with this type of logic?