350A - TL

Пусть v = min(a_i), p = max(a_i), c = min(b_i). Тогда если max(2 * v, p) < c, то ответ max(2 * v, p). Иначе ответ  - 1.

Авторское решение: 4632352

350B - Курорт

В этой задаче достаточно было реализовать следующее. По сути там задан граф, в виде массива предков для каждой вершины. Поскольку у каждой вершины максимум один предок, то для каждой вершины, являющейся отелем запустим такой алгоритм: будем подниматься по предкам prev[v] до тех пор, пока не встретим вершину со степенью исхода большей единицы. Степень исхода лучше посчитать заранее. После всего обновим ответ.

Асимптотика решения O(n) по времени и O(n) по памяти.

Авторское решение: 4632399

350C - Бомбы

Главная идея, это отсортировать все точки в порядке возрастания величины |x_i| + |y_i|. Дальше будем обрабатывать каждую точку жадно, максимум за шесть ходов. А именно, пусть мы хотим дойти сейчас до точки (x, y). Пусть x ≠ 0. Тогда нам нужно переместиться ровно на |x| в нужном направлении (если x < 0 то по направлению L, x > 0 — R). Аналогично сделаем для y-координаты. Теперь мы пришли в точку (x, y), возьмем в этой точке бомбу, и аналогично вернемся назад. Почему верно сортировать по так называемому манхэттенскому расстоянию? Понятно, что если мы посмотрим на путь, который мы получили, можно заметить, что все точки пути имеют меньшее манхэттенское расстояние, а значит их мы обработаем раньше.

Асимптотика авторского решения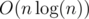

Авторское решение: 4632478

350D - Поиск сов

Будем решать задачу в целых числах. Поэтому всегда будем строить прямую в целых числах. Операцией нормализации прямой будем называть следующее: Пусть у нас есть прямая Ax + By + C. Пусть также g = gcd(A, gcd(B, C)) (gcd(0, 0) = 0).
Если А < 0 (или A = 0 и B < 0), то умножим уравнение на -1 и поделим все коэффициенты на g.

Теперь решение. Будем поддерживать два отображения (map<> на С++, TreeMap(HashMap) на Java) из прямой, в множество точек (некоторые точки могут встречаться несколько раз). В первом отображении в качестве множества точек мы будем хранить левые границы отрезков, во втором правые границы отрезков (в отсортированном виде).

Заранее по каждому отрезку построим прямую, нормализуем ее, и поддержим наши указанные выше множества множества. Далее, для каждого возможного уравнения отсортируем указанные множества.

Теперь переберем две окружности. Проверим, что расстояние между их центрами больше суммы радиусов и что радиусы одинаковы. Пусть мы построили прямую через центры (x1, y1) и (x2, y2). Перпендикулярная ей прямая, проходящая через центр отрезка [(x1, y1), (x2, y2)] будет иметь уравнение A = 2(x1 - x2), B = 2(y1 - y2), C =  - ((x1 - x2) * (x1 + x2) + (y1 - y2) * (y1 + y2)). После этого бинарным поиском по множеству точек, соответствующих указанной прямой, найдем две величины: cntL — количество отрезков, у которых левая граница правее ((x1 + x2) / 2, (y1 + y2) / 2) и cntR — количество отрезков, у которых правая граница левее ((x1 + x2) / 2, (y1 + y2) / 2). Тогда к ответу нужно прибавить величину cntV - cntR - cntL, где cntV — количество отрезков соответствующих заданной прямой в отображении.

Итого, решение за .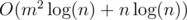

Код: 4632546

350E - Неверный Флойд

Решение задачи очень простое, главное придумать почему это верно. Будем действовать так: построим граф с максимальным возможным количеством ребер, потом удалим лишнее. Во-первых, если k =  = n, то ответ -1. Иначе зафиксируем некоторую помеченную вершину, например a₁. Возьмем в наш граф все ребра, кроме ребер вида a₁ <  -  > x, где x — помеченная вершина. Теперь почему так действовать верно. Если алгоритм Валеры работает неверно, значит существуют пара вершин (i, j) такая, что кратчайшее расстояние посчитано неверно. Значит, на кратчайшем пути из вершины i в вершину j есть хотя бы одна не помеченная вершина (причем, что важно, она не должна совпадать ни с i, ни с j. Если бы такой вершины не было, кратчайшее расстояние посчиталось бы верно. Более того, не нарушая общности, будем считать, что кратчайшее расстояние между i и j равно двум, а алгоритм Валеры нашел больше. Далее, для более формального доказательства нужно рассмотреть случаи, в зависимости от того какой тип имеет каждая из вершин (i, j), однако я рассмотрю случай, когда мы получим больше всего ребер, а именно когда и i, и j — помеченные вершины (а их по условию всегда не меньше двух :)). Во-первых, проведем все ребра во между не зафиксированными ребрами. Дальше проведем и из i и из j ребра в не помеченные вершины. После этого проведем из i все ребра в помеченные, кроме вершины j. Понятно, что больше добавлять ребер нельзя, так как иначе алгоритм Валеры посчитает все верно. Таким образом, мы проведем ровно 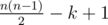ребер.

Код: 4632600

BONUS Простой бонус. Можете ли вы для аналогичных входных построить граф, где алгоритм Валеры будет работать верно?