Здравствуй, сообщество Codeforces!
Через несколько минут стартует очередной этап Открытого Кубка.
Предлагаю обсудить задачи после контеста здесь.
GL & HF!
P.S Если что, начало раунда было перенесено.
UPD Раунд перенесли еще на 15 минут полчаса. Обещают начать в 12.45 MSK в 13.00 MSK











Как можно попасть в систему?
Сайт соревнования. Нужно иметь логин (получать у координатора сектора).
[не очень смешная картинка, которая мешает обсуждению задач]
Ну что, craus пришел, можно уже начинать
http://bombermine.clay.io/
Превратили бомбермен в какое то говно, извиняюсь
Мне вот обидно, что игру развивают-развивают, а она до сих пор тормозит, с большим полем нельзя получить стабильные 60 FPS, да и задержка ввода большая. Хотя надо признать, раньше было ещё хуже.
Ее НЕ развивают, в нее какую то херню добавляют. Какие-то футбольные мячи, радужные котятки, пакманы. И зачем? Обычный дефолтный бомбермен намного лучше.
Кто-то верит в перспективу бомберов? У кого-то получилось играть больше получаса? В нее О(1) людей поиграли О(1) времени, и забыли.
Я немало играл, когда он только-только вышел и не было всей этой чепухи
Дуров, верни стену.
Ох уж эти задержки ><
Еще один перенос на 15 минут.
div1, div2
у всех в ejudge вошло?
А табличка для болельщиков будет?
А где команды из итмо?
Upd: Появились Оо
Как надо решать F?
А доказать как? сабмитом? :)
Доказать фразой Паши "да сабмить, это по-любому зайдет"
Биномиальное распределение, нас интересует его медиана. А вот в то что данная структура в рамках данной задачи соответствует p_i = p_j = (L / N) * (M / N) это уже интуитивные соображения.
Алгоритмический подход к решению: переформулируем задачу, пусть первый выбрал какие-то l чисел, а второй пытается эти числа угадать за m попыток. Без ограничения общности, будем считать что первый ткнул в числа 1..l; тогда вероятность того что второй угадает ровно k чисел p(k) = C(k, l)*C(m — k, n — l)/C(m, n). Тогда нужно найти такое k, что сумма на префиксе будет примерно 0.5 . Выпишем формулу как пересчитывать ответ для k через k-1 (распишем цешки и получим дробь, на которую нужно умножить при переходе). Чтобы не было проблем с точностью, считаем не p(k) а log(p(k)) (операции у нас только умножить/разделить, которые легко заменяются на плюс/минус). Ну а дальше считаем сумму на префиксе и проверяем что она больше 0.5:)
Ну, можно её решить и без интуитивных соображений. То, что точно решать не надо (т. е. ответ может отличаться на 10) намекает на то, что можно добиться успеха простой симуляцией. Мы можем посчитать для фиксированного K какова вероятность его получить: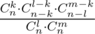 . Идём себе по k и жадно прибавляем эту величину, пока она не превзойдёт 0.5, не забываем, что чтобы ничего не переполнилось, числитель и знаменатель вычислять явно не надо, например, можно посчитать дробь в логарифмах и взять экспоненту.
. Идём себе по k и жадно прибавляем эту величину, пока она не превзойдёт 0.5, не забываем, что чтобы ничего не переполнилось, числитель и знаменатель вычислять явно не надо, например, можно посчитать дробь в логарифмах и взять экспоненту.
И знать никаких соображений про биномиальное распределение не надо.
UPD: ой-ой-ой, я не увидел коммента JKeeJ1e30, который рассказывает ровно то же самое.
А у вас в дроби получилось 5 цешек. У меня всего 3:). Разумеется, если посокращать, получится одно и то же, просто интересно:)
Мы так и делали, только про логарифм забыли :(
Мы тоже о нем вспомнили только на последнем часу:). Хотя, казалось бы, очевидно что его нужно применить.
Какая сложность авторского решения в Н?
Меня терзают смутные сомнения по поводу того, нормально ли, что у меня N^3*Q зашло. Не какое-нибудь Q*N^3/32 с битовыми оптимизациями, а простое такое Q*N^3)
Естественно на плюсах? :)
у нас O(Q * N2), мы считали sum[i][j] — количество путей из i в j по модулю 109 + 7, и если эта величина равнялась нулю, то считали, что ребра между i и j нет
Я подумал, что считать по модулю может быть несколько медленно. Есть другой вариант того же решения.
Будем каждому добавляемому ребру присваивать рандомное нечётное число — назовём это весом. А весом пути назовём произведение весов его рёбер. Будем поддерживать матрицу: A[i, j] — сумма весов всех путей из i в j по модулю 232. Если я не ошибаюсь, то это можно аналогично пересчитывать, но нигде ничего не нужно делить.
Upd: наверное, надо было назвать это кратностью...
По модулю 232 не должно работать. Есть графы, в которых ровно 232 путей между вершинами.
UPD: Степа меня уже переубедил. Заваливать это решение я не умею. Но объяснять, почему работает, тоже не умею.
Не очень понятно, что вы делаете при добавлении нового ребра?
Там не очень сложно пересчитываются эти величины. Обрабатываем сразу все ребра, которые добавлены из вершины v. Тогда к sum[i][j] нужно прибавить sum[i][v] * (sum[a[0]][j] + sum[a[1]][j] + ... + sum[a[k - 1]][j]), и вторую скобку для каждого j мы можем предпосчитать. Добавление ребер в вершину и удаление делается по аналогии.
Вроде не должно было.
У жюри было два AC решения: QN3/32 (понятно, как) и QN2 (ровно то, что описал Kostroma)
Вышли, пожалуйста, код на Burunduk30@gmail.com.
Решение 16*10^8 — то еще авторское решение. Мы, посчитав асимптотику, решили не писать такое. Казалось бы, такое решение завалить проще простого — нагенерить полный граф из n*(n-1)/2 ребер с ориентацией так чтобы циклов не было, и запросы удаление/добавление небольшого числа ребер, по сути не меняя граф. Такие тесты были? Слабо верится, что на таких тестах быстро отрабатывает, учитывая асимптотику
Оказалось, что это на джаве за секунду работает)
10^9 битовых операций. Почему бы не отработать? Тем более, там кажется TL был большой.
Битовых операций 10^11, 10^9 — это уже с делением на 32 асимптотика:)
Я имел ввиду что 10^9 операций вида "сделай and двух чисел и присвой в третье" Это очень быстро, в кеше, и параллелится неплохо на уровне процессора.
Ну не 16*10^8, а 8*10^8, так как ребер, как ты сам сказал — n*(n-1)/2. Еще нужно учесть, что граф станет полным лишь после n запросов, то есть половины от их общего количества, и что мы просто делаем побитовое "или" двух чисел.
Были такие тесты.
800 * 4002/2 * 400/32 = 8*108 операций вида OR с последовательным обращением к памяти. TL = cpp 3 (java 8).
P.S. С точки зрения тактики: я бы в такой ситуации не думал, а написал бы цикл от 1 до 8*108 и посмотрел бы, сколько он работает.
У нас первая команда сдала O(QN3) с битовыми масками. Они смогли это сделать в основном потому, что свято верили, что у них работает за O(QN2). После конца тура их конечно быстро разочаровали...
400^3 * 800 = 10^11 — нормально:)
Я уже отослал исходник Burunduk1. Будем после каждого запроса строить конденсацию графа (ну да, можно не конденсировать, я только за 20 минут до конца прочел, что граф ациклический), топсортить ее, и после этого считать динамику reach[i][j] — "достижима ли вершина j с вершины i", обходя вершины в порядке топсорта — для каждой вершины отмечаем как достижимые все вершины, которые достижимы с ее сыновей, а так же отдельно сыновей. N вершин обработать, у каждой до N сыновей, апдейт для каждого из этих сыновей за N (или за N/const, если битовыми операциями, у меня без них). Отсюда N^3 на запрос.
Ну да, все то же самое что и у всех остальных, только без битовых операций. В общем, печальбеда, что такое заходит.
Справедливости ради — у меня есть сабмит в 4:59:40, который использует битовые операции, и тоже получает АС. Последние штук 6-7 сабмитов по этой задаче я делал вслепую, так как очередь висела и я не знал вердиктов) Ну и еще у меня там что-то нашаманено с различными if'ами и порядками циклов, может в этом какой-то прикол. Я отсылал много различных вариантов, которые получали ВА или ТЛ на разных тестах.
В тред вызывается Петр, дабы поведать общественности как делать задачу D.
Я не Петр, но отвечу)
Мы запихали следующее:
1)Делаем понятно что за 2^26*26 (сначала сгенерируем все проигрышные позиции-надмаски масок букв в словах, потом пройдем с конца к началу по массиву масок и проверим для всех позиций какими они являются).
2)scanf — это очень плохо, используем gets()
3)Буквам сделаем random_shuffle.
4)Оптимизируем первую часть. Перебираем строки инпута по одной, добавляем для каждой маски ее надмаски с отсечением, что если мы наткнулись на уже отмеченную надмаску, то перебирать надмаски этой надмаски не нужно (это некоторая магия с битовыми операциями и __builtin_clz(), код сейчас показать не могу).
5)Основную динамику можно делать "вперед", а можно "назад". Один из этих способов у нас получил TL65, второй AC.
Очень надеюсь, что авторское решение никак не связано с подобными преступлениями)
За счёт битовых операций можно с 2^26*26 ускорить до 2^22*22+2^26*4. Это все ещё небольшой TL — зашло после убирания ifов во внутренних циклах.
Авторское решение работает за 226·26 / 32. То, что сдали две команды, насколько я могу понять — это нечто среднее между медленным решением за 226·26 и быстрым.
Отметим подмножества, заданные словами. Придумаем медленную динамику в два этапа.
(1) Для каждого подмножества букв снизу вверх, если оно запрещённое, распространим это на все его ближайшие надмножества:
Заметим теперь, что запрещённые подмножества можно считать выигрышными для тех, чья очередь хода при нахождении в них.
(2) Для каждого подмножества букв сверху вниз, если оно проигрышное, сделаем выигрышными все его ближайшие подмножества:
Это решение использует булевский массив
fи работает несколько секунд — слишком медленно. Предлагаемая оптимизация — векторизовать битовые операции так, чтобы за одну операцию с int32 выполнялось 32 нужные нам операции с булевским массивом, упакованным в битовый массив. Теперь вместо элемента массиваf[s]мы будем пользоваться битомg[s >> 5] & (1 << (s & 31)).Для переходов по
j >= 5наша динамика отлично подходит, например, из первой части получается следующее:Такой код за одну операцию действует одновременно на вектор из 32 битов. Например, если
t = 0иk = 0, действиеg[t ^ (1 << k)] |= g[t];(то естьg[1] |= g[0]) эквивалентно следующим 32 действиям медленной версии:А вот вместо троеточия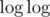 диапазона, то есть за 5·C действий, так:
диапазона, то есть за 5·C действий, так:
<...>нужно сделать переходы, которые раньше происходили приj < 5. Это менее тривиально. В первой динамике это можно сделать заЗдесь
0bXXXX— двоичные константы. Например, второе действие выполняет следующие 16 эквивалентных действий с булевским массивом:Но, во-первых, это не очень быстро, а во-вторых, вторая динамика сложнее, и такой подход будет ещё более трудоёмким. Так что для троеточия
<...>будем использовать другую идею. Заметим, что наша динамика монотонна: в первой динамикеf[s]влияет только наfс индексами> s, а во второй — только наfс индексами< s. Придумаем троеточие<...>для второй динамики, а для первой получится аналогично.Итак, что происходит внутри одного g[t] во второй динамике? Сначала верхний бит (с номером 31) как-то влияет на биты 30, 29, 27, 23 и 15. Затем следующий сверху бит (с номером 30) как-то влияет на биты 28, 26, 22 и 14. Далее следующий бит (с номером 29) как-то влияет на биты 28, 25, 21 и 13, и так далее. Ещё очень важно, что единственный способ влияния — операция ИЛИ, то есть единички могут только появляться.
Разобъём g[t] на верхний и нижний куски по 16 битов. Тогда происходящее внутри g[t] можно разбить по времени на два отрезка:
(1) верхние 16 битов влияют на значение g[t] (на все 32 бита),
(2) нижние 16 битов влияют на значение g[t] (фактически только на нижние 16 битов).
Для каждых возможных верхних 16 битов предподсчитаем, как они повлияют на значение всех 32 битов — фактически получится маска из 32 битов, которую нужно по-OR-ить с
g[t]. Запомним эти маски в массивеhi [1 << 16].Затем для каждых возможных нижних 16 битов предподсчитаем, как они повлияют сами на себя — получится ещё одна маска. Запомним её в массиве
lo [1 << 16].Теперь, если у нас есть
g[t]до применения к нему динамики, то мы можем быстро узнать, каким он станет после применения к нему динамики. А именно, пустьg[t] = (x << 16) + y, где0 <= x, y < (1 << 16). Преобразования будут таковы:Конечно, значение
yнужно вычислить уже после выполнения первой строчки, так как оно могло измениться.Итак, мы научились всего за два действия применять преобразования второй динамики к 32-битному элементу массива
g[t]. Итоговая версия второй динамики после предподсчёта такая:Для первой динамики нужно, наоборот, сначала влиять нижними битами на нижние и верхние, а потом верхними на самих себя. Сам предподсчёт каждого из массивов lo и hi можно сделать медленной динамикой за 216·32.
Вот полный пример кода, реализующего эту идею. Авторские решения работают за 0.5 (C++), 0.7 (D) и 0.9 (Java) секунды на проверяющих серверах. Ограничения по времени выставлены не очень жёстко (2 для всех языков и 3 для Java), что (учитывая ещё не очень умно сделанные тесты) позволяет пройти достаточно оптимизированным промежуточным решениям.
в C были тесты с K==2? мы выводили просто минимальную длину между двумя, а не удвоенную, и получили OK.
Нет, не было =)
На самом деле, более правильный ответ на клар таков: k ≥ 3.
Сразу несколько вопросов по задаче С :) Какое предполагалось авторское решение? Сколько всего было тестов? Как генерировались авторские ответы (то есть как было показано, что они правильные)?
=)))
Авторское решение, если коротко: жадно приближаем ответ взяв для каждой точки k ближайших, затем полный перебор с отсечением по ответу. Подробно сейчас напишу.
Тестов всего 66.
Из "полный перебор с отсечением по ответу" следует, что работает корретно (если багов нет). На всякий случай стрессилось с полным перебором без отсечений и переборами с более простыми отсечениями.
Забавно, мы написали много разных эвристик, большинство из них давали ВА 59, но поменяв рандсид мы получили сразу несколько новых ВА: ВА 64 и ВА 66. Интересно, чем эти рэндомные тесты принципиально отличаются от других. Локально наше решение находило ответ очень быстро.
Не поверишь =) Они отличаются только randseed-ом.
057 : ./gen_random.exe 239073 60 15 1000
058 : ./gen_random.exe 239074 60 15 1000
059 : ./gen_random.exe 239075 60 15 1000
060 : ./gen_random.exe 239076 60 15 1000
061 : ./gen_random.exe 239077 60 15 1000
062 : ./gen_random.exe 239078 60 15 1000
063 : ./gen_random.exe 239079 60 15 1000
064 : ./gen_random.exe 239080 60 15 1000
065 : ./gen_random.exe 239081 60 15 1000
066 : ./gen_random.exe 239082 60 15 1000
Какой перебор?? Там же очевидная динамика по выпуклой оболочке...
Забавно. А я хотел что-нибудь переборное придумать... Значит, не получилось. Но вот одна команда в перебор точно поверила ))
Мы вот тоже в перебор поверили:) В итоге с 3 попытки зашло.
А почему с третьей? Вроде тестилась задача просто на ура — генерируешь случайные точки и смотришь TL. Сравниваешь с полным перебором и смотришь WA.
Потому что это был перебор вида "давайте 2,5 секудны (в случае джавы) понаходим что-нибудь и выведем лучший результат". Ну и в первых двух попытках он не успел найти оптимальное решение, а в третьей добавили отсечение типа "если периметр четырехугольника, построенного на самой левой, самой правой, самой нижней и самой верхней точках больше текущего ответа, то не будет рассматривать такой набор точек" и этого хватило.
А сам перебор был такой: возьмем рандомную точку. Рассмотрим круг минимального радиуса в которых входит, например, 22 точки. Перебер каждый сабсет содержащий ровно k точек из этих 22, построим выпуклую оболочку и обновим ответ.
Хм. Видимо, стоит пояснить.
Да, я считаю, что на контесте перед сабмитом полезно тестить =)
В данной задаче, если уж, участники писали перебор, то у них был на руках работающих полный перебор. Мысленно напишем еще один цикл for, получим генератор случайных тестов.
Как ловить WA, который WA? Полминуты пострессить на маленьких тестах с полным перебором.
Как ловить WA, который отсечение по времени? Запустить 10 раз на случайных тестах c TL = 1s, TL = 5s и сравнить.
Вопрос: зачем посылать в систему, если и так легко понять, работает, или не работает?
Да, согласен, надо было так потестить.
Расскажите!
Лемма 1: среди всех множеств, в которых ≥ K точек, минимальный периметр выпуклой оболочки имеет некоторое, в котором ровно K точек.
Теперь решение: фиксируем нижнюю левую точку, которая лежит на выпуклой оболочке. Убираем всё снизу, остаток сортируем по полярному углу. Теперь запускаем стандартную динамику поиска выпуклых многоугольников: последняя вершина такая-то, уже набрали столько-то точек (и на границе, и внутри). Квадрат состояний, переход за линию (надо еще предподсчитать точки внутри каждого треугольника).
Таком образом найдём какой-то многоугольник минимального периметра, в котором нестрого внутри лежит ровно K точек. Докажем, что любой ответ выражается в таком виде. В самом деле, пусть в ответе мы берём не все точки, лежащие внутри. Тогда давайте возьмём одну невзятую точку изнутри и выкинем одну с границы. Периметр не уменьшится, зато станет меньше невзятых точек внутри. По индукции получим, что наша динамика нашла ответ.
Код
спасибо! Вроде понял! А можно еще парочку задач в придачу для закрепления материала?
Очень похожая была на заключительном этапе заочной олимпиады по программированию 10/11 года.
А как код с контеста восстанавливать?
Я скопировал после контеста на флешку. Еще можно попробовать достать с сетевого диска (если его не прибили), либо напрямую из Testsys.
Ром, а правда, что задача "минимизировать сумму попарных расстояний" динамикой уже не решалась бы? Перебору то, конечно, по фиг...
Да, кажется так просто не получится... А перебору конечно все равно)
Авторское (мое) решение:
Запустили жадность "для каждой точки выбрали k ближайших". Получили хорошее приближение ответа.
Перебор go(сколько точек взяли, последняя выбранная, множество) со следующими отсечениями:
(1) Запоминание от множества
(2а) Если текущий периметр хуже, сразу вышли
(2б) Нам нужно добавить еще k-i точек. Пытаемся добавить их по одной, получили n-i периметров. Ответ будет не меньше чем k-i минимальных из данных n-i чисел.
(3) Теперь перебираем, какую точку добавить, и собственно добавляем. При этом:
(3а) Если какая-то точка попала в выпуклую оболочку, берем ее.
(3б) Добавляем точки в порядке возрастания номера.
P.S. Время работы 0.125 секунд
P.P.S. Задача делалась так: я добавлял отсечения, пока не счел задачу достаточно сложной. Охотно верю, что можно еще сильно улучшить.
Забавно.
У нас решение базировалось на том, что если взять прямоугольник, в котором лежит выпуклая оболочка, то внутри него будет мало точек, не лежащих в оболочке. Потому сгенерируем все прямоугольники, в которых лежит между К и К + magic точек, затем для всех таких множеств точек переберем все подмножества из К точек. (На практике c magic = 2 зашло, будет дорешка — попробую 1 и 0)
Я еще подумал, что все так логично, как раз перебрать все прямоугольники за 5ю степень вкладывается в ТЛ, а факт, что вероятность нахождения точки вне оболочки, но внутри прямоугольника, низка, наверное доказывается несложно.
А тут на тебе:)
k ≥ 3 ? Интересно. Мы сперва отправили решение и получили WA49, после этого добавили заглушку на k = 1 и получили ОК.
Кстати а в задаче K TL для Java был именно такой, какой указан в условии? Потому что в задаче H он изначально был неправильный, а потом все тихо пореджаджили.
А, чёрт, а я оптимайзил сидел H :(
When does the upsolving begin?
А как решать задачу G?
А как решить А за 1 минуту? (см. 75 место)
Перейдем к системе счисления с основанием 1001. Тогда если мы взяли a[1] платиновых медалей, a[2] золотых и т.д., то представим это в виде a[1] * 1001^9 + a[2] * 1001^8 + ... + a[10]. Эту величину нужно максимизировать. Если человек i идет на дисциплину j и приносит медаль достоинства k, то стоимость ребра из i в j 1001^(10 — k). Теперь просто нужно найти паросочетание максимального веса. Решаем минкостом.
G = mincost flow.
Вес ребра — вектор длины "количество медалек". Для ускорения можно веса сжать в два 64-битных числа.
Заходили и ford-bellman и dijkstra.
Подробнее рассказывать?
Блин, заходило. Понятно :(
Получить задачи до старта контеста?
Есть ли работающие ссылки на итоговые таблицы для див1 и див2?
А как характеризовать плоскость на двух векторах в d измерениях для задачи К?
В смысле?
Решается так: зафиксировали один вектор, вычли его из остальных, как в Гауссе, после этого оставшиеся вектора нужно разбить на классы колинеарных, для этого приведем их к инвариантному виду (поделим на первую не нулевую координату) и отсортируем.
Спасибо, ясно, действительно, очень просто. :) А мы просто хотели для каждой возможной плоскости найти все пары векторов, которые образуют эту плоскость. Поэтому была необходимость привести плоскость в какую-то нормальную форму.
У нас зашел пропих хэшей правильно ориентированных единичных перпендикуляров к одному из двух векторов плоскости, где перпендикуляр также лежит в плоскости. Хэш считался просто как полином от координат вектора, домноженных на степень десятки и округленных. Вычисления в double упорно давали WA52, после использования long double прошло.
Мы придумали вот так характеризовать плоскость: зафиксируем две случайные точки в d-мерном пространстве, и найдём на каждой плоскости ближайшую точку к каждой из них. Ближайшая находится как минимум квадратичной функции по двум переменным, через решение системы двух линейных уравнений (производные приравниваем нулю).
А вы точки вычисляли в рациональных? Не было проблем с TL?
В даблах, потом брал Math.floor(a[i] / 1e-10 + 0.some_random_number).
Нам пришлось в конце тоже самое сделать. А в рацональных не успевало из-за взятия gcd :)
У жюри есть AC решение на cpp в рациональных. Чтобы проходило по времени, достаточно GCD брать один раз в конце =)
В конце чего? :)
У нас решение ровно такое как у Petr'a, Только систему мы решали в рациональных числах. После этого вычисляем точку (10 рациональных чисел). x_1/a, x_2/a, ... x_10/a. В этот момент я и вызывал gcd(x_i, a) = d_i. После, я считал от нее (вернее от двух таких точек) хэш, как от наборов чисел: числители и знаменатели.
http://pastebin.com/Lciz7VJd
У кого было ВА4 в задаче B (Шашки)?
у меня...
Она у вас прошла? Если да, то что в этом 4ом тесте было?
нет не прошла, самому тоже интересно. Вроде легкая задача
Как она вообще решается?
перебором над количеством партий(1 или 2), например для 4:
1111
112
121
211
22
Решал перебором: http://pastebin.com/GztrXCNC Можете посмотреть код?
тест:
1 2
W
Честно говоря, было очень неприкольно ждать 1 час 15 минут до начала контеста. Одна из Саратовских команд вообще не выдержала и ушла до начала. Первые полтора часа контеста у нашей команды не отображался общий монитор. Как сказал один из саратовских участников, это просто неуважение к участникам. Многие люди распланировали свой день, им пришлось либо менять планы, договариваться об отмене заранее назначенных встреч, либо не писать контест/уходить с него в середине. Неужели так сложно было изначально проверить решения, систему? Почему все нужно делать в последний момент? Я понимаю, что приготовить качаственный контест — задача непростая. Но почему-то большинство авторов с этим справляются. Заранее благодарю за ответ.
Ага, вышло примерно так же. Осталась только наша команда и координатор, который ютуб смотрел :)
как можно досдавать?
А есть ли результаты где-нибудь?
Олег кажется уронил http://acm.math.spbu.ru:8087
От туда скорее всего уже все уехали, и с учетом того, что он сам не поднялся, видимо до завтра не будет. Результаты чемпа вот http://acm.math.spbu.ru/cgi-bin/monitor.pl/m131006.dat Думаю скоро разморозят. У нас 10, у банановых 9, что еще интересного я не знаю. Штраф минут на 40 хуже, чем у вас. Надо было все с плюса сдавать.
Спасибо!
Гдето можно участьвовать виртуално?
А кто писал на Яндексе? Как зайти в этот контест, у нас так и не отобразилось соревнование. Пробовали opencup.contest.yandex.ru.
Пока что на Contest писали несколько команд ИТМО и США. Мы будем постепенно приглашать больше команд участвовать на Яндекс.Contest.
Официальный разбор данного гран-при можно будет найти?
почему многоуважаемый г-н не откроет дорешку?!
Дорешку открыли
Можно ли где-нибудь посмотреть сколько очков у нашей команды?
The checker for problem I (Revolving Lasers) contained a bug which made it reject certain valid moves.
The bug is now fixed, all submissions in all relevant contests were rejudged.
This bug affected two teams at the top of Div1.
Sorry for the bug, and for being so slow finding it.
А как был устроен чекер к задаче по змею, если не секрет?
Вроде мне сказали, что там какая-то жесть на 900 строк, которая проверяет какие-то инварианты, которых достаточно из-за странных условий на количество и тип пересечений.
Очень хотелось бы взглянуть на эту штуку. И на восьмой тест :) А то эвристика, которую мы на контесте доказали, на восьмом как раз падала долго и упорно.
upd: Как подсказал Паша, неправильно мы эту эвристику доказали, и она действительно вполне может падать.
Чекер для змеек считал простой алгебраический полином (полином Джонса), который является инвариантом узла (и зацепления). Это значит, что если полином Джонса двух зацеплений не совпадает, то они разные. Обратное утверждение в общем случае неверно. Но оно верно при числе перекрестков меньше либо равно 7. Поэтому в условии и было странное ограничение n<=7. Перекрестки имеются в виду такие, как в условии задачи, под узлом подразумевается одна змейка, под зацеплением — несколько змеек. Часть теории и ссылки могу куда-нибудь положить. Подсчет простого алгебраического полинома закодился у меня почему-то в 900 строчек примерно, хотя на бумаге он выглядит просто. Чекер содержал баг, который проявился на кубке, в функции считывания зацепления (это когда несколько змеек), не математический, а неправильный ввод из файла при считывании зацепления. Он отражался только на ситуации зацепления (нескольких веревок), а не узла (одной веревки). Восьмой тест — это узел. А какая все-таки эвристика?