I have an AC solution with following idea, but I could not proof the correctness myself:

Use all Unmarked vertex to form a "wall" to separate 1 marked vertex V0 and the others, it can always be done as k >= 2 and pre-check k < n (as when k==n, there is no solution obviously)

So now we have 3 set of vertex: {v0}, {unmarked vertex}, {marked vertex \V0}

Link them up using n-1 edge to conserve the "connected graph" property, it can also be done as m >= n-1

I have drawn a picture to illustrate the idea (bare with my MSpaint skill :O) )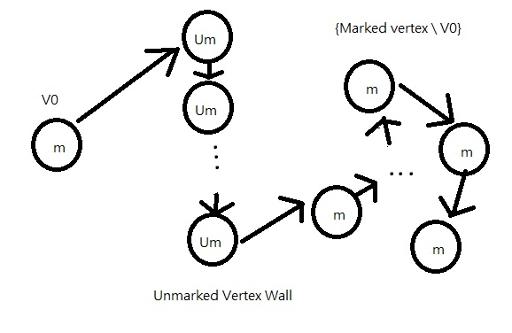

for more edges, just link any vertex p,q, except p belongs to {V0} and q belongs to {marked vertex \V0} (or vice versa)

With this method, V0 is always "unseen" to {marked vertex \V0}, which means having INF range

so, for n-1 <= m <= (n-1)(n-2)/2 + (n-k), I can always construct a graph which is the solution,

I claim for (n-1)(n-2)/2 + (n-k) < m <= n(n-1)/2 , there is no solution.

I cannot proof the last claim though...Anyone could help? :(