Given a polygon $$$n (n \leq 10 ^ 5) $$$ vertices on a 2D Descartes plane. $$$(|x_i|,|y_i| \leq 5. 10^8)$$$. This polygon is not self-intersecting, 2 consecutive edges have only 1 common point (which is the vertex). Find the sum of all segments of the 2D plane lie completely inside the polygon. (can be a real number).
Input:
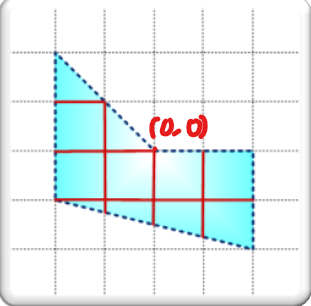
5
0 0
-2 2
-2 -1
2 -2
2 0
Output: 12.5
Explain: The answer is the sum of all the red segments. The middle point is $$$(0,0)$$$.











Do a sweepline for both directions.
Going from bottom to top, keep all active segments in a sorted container. We will now process events and lazily add up the contribution of each line. For this you also need some meta information for each line, whether the polygon is to the right, or left and upto which height its contribution has already been added.
An event is either the start/end of two neighboring segments or replacing a line by another line. You can now update the sorted container. When doing this remember to add up the remaining contribution of previous segment at this position. This is just arithmetic so I won't go into detail. Furthermore don't forget to handle the case of a line parallel to the x-Axis.
Thanks for answering! Could you elaborate your idea with the above test case please? Appreciate!
Ok I first lets go from left to right.
Initially we add the lines (-2, 2)->(0,0) and (-2,1)->(2,-2). Remember vertical/horizontal lines need to be special cased. Next the line (0,0)->(2,0) will start. This line replaces (-2, 2)->(0,0), so we have to add its contribution. In this case this is the segment (-1,1)->(-1, -1.25).
Now we have [(-2, 2)->(0,0); (-2, 2)->(0,0)] in our container and know between them is the polygon and we need to start counting at x = 0.
Then we consider the segment (2,0)->(2,-2) which merges (i.e. removes) the lines (-2, 2)->(0,0) and (-2, 2)->(0,0). Therefore we have to add their remaining contribution, which are the segments (0,0)->(0,-1.5) and (1,0)->(1,-1.75). Since we considered all lines we are done.
Remember, we can't add all contributing lines one by on. Instead we have to compute the current contribution in O(1). For this let $$$\Delta y$$$ denote the left most distance between the segemnts and let $$$\Delta y_1$$$ denote the difference in distance per step. Then if $$$l$$$ is the length we have
.
Sorry but may I have a few absurd question?
When do we add/delete/replace lines in our container?
How that there is 2 same lines in our container [(-2, 2)->(0,0); (-2, 2)->(0,0)] ?
$$$\Delta y$$$ denote the left most distance... What do you mean by left most distance? (A real example would be great.)
$$$\Delta y_1$$$ is the distance per step. I don't understand. Could you give an example?.
Is $$$l$$$ the difference of x coordinate between the current event and the last one?
I think you can use something similar to the calculation of the area of a polygon using trapezoids. We calculate what the signed sum of the lengths of all the vertical lines that lie inside or on the right boundary of a trapezoid is.
The formula is $$$sgn \cdot ( W \cdot P.y + (W+1) \cdot (Q.y-P.y)/2 )$$$, where $$$W = abs(Q.x-P.x)$$$ and $$$sgn$$$ corresponds to the sign of the area of the trapezoid.
If for every edge in the polygon we add the signed sum of lines of its trapezoid up, I think we get the answer. Vertical edges are a special case and sometimes we have to subtract them out, to stop overcounting of right boundaries of trapezoids. This only counts the vertical lines, so we rotate the polygon 90 degrees and do it again.
It seems to me that your solution won't be able to pass the below case. Sorry if I missed something.
I think my approach could work on your test, because when you calculate the contribution of a trapezoid formed by an edge of the polygon and the x-axis, sometimes this contribution is positive, sometimes negative which cancels all the lines outside the polygon and sums precisely the line segments inside the polygon. I made a program implementing my idea for this problem. It works on your example, but I didn't test it further:
Thanks so much. Your approach is no neat. Unfortunately, the three big test case didn't match your output (the remaining 17/20 works). I don't know why, maybe the testcase was poorly generated.
You can check the three testcase here: https://drive.google.com/drive/u/0/folders/1WdIhtuiy5hML6x2tFmOe6iBQ6KdV4j3I
Can you share the problem link?
I don't know if it is online or not. I have about 20 local tests for this problem.
Thanks for everybody. Using your ideas and suggestions, I have come up with a weird solution. (It outputs correct for 17/20 test cases — the 3 remaining are huge ones and I don't know what to do — maybe just assume that the test output is wrong by float/double/long double reasons).
At first I think about sweepline 2 directions and calculate like Veladus ideas. But I stucked at the polygon which is like the picture below. As we each time we get to an event there can be O(n) different trapezoids (and it seems that there is hardly a way to manage every trapezoid and sum up all of them at once).
So I changed the idea a bit. First I took the convex hull of the polygon. And calculate with the above idea. But it will be redundant of course. So I just iterate through the polygon again and find which inner-polygon is redundant and recursively solve it again then minus the redundant part. It is a lot of implementation, though.
I thought it would be slow, but in fact it was fast but it was WA.
I'm looking for a way to generate testcase for this problem. But the restrictions of polygon which is not self-intersecting and the input have to be ccw/cw order, makes it really hard. Not only that I don't know how to have correct output for that generated testcases :'(.
I'd appreciate if anyone suggest me a way to generate test and help debug my code.
What about triangulation?
As I see you can easily calculate answer for triangle in $$$O(1)$$$. Then find any triangulation and sum up all the answers. The only case is when sides are parallel to axis (e.g. square, rotated pi/4)
That's an idea to consider. However, as I'm fed up with this problem, you can try to implement your approach and check the above 3 big testcases google drive link. (If you are successful, please show me your code <3. Thanks)