phuthuynhochienthan's blog

Some problems from team selection test
By phuthuynhochienthan, 11 years ago, In English

I have taken part in the team selection test of my school for Olympiad and there are some difficult problems remaining unsolved during this contest. Hope some one can help me with the outline idea, thanks so much!

Problem 1.

Let S be a string with length |S| <  = 104 and S1, S2, ..., Sk are all distinct sub-strings of S (sub-string of S can be received by deleting some or all characters from S). Let fi be be number of occurrence of sub-strings Si with 1 ≤ i ≤ k. Find the total 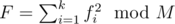in which 2 ≤ M ≤ 109. There are T ≤ 50 tests and each test includes string S and number M. Example:

input:

2
zoo
10
@#$%
1000000

output:

2
16

Problem 2.

Let (an) be a positive integer sequence and a key X be a positive number. Count the number of ordered triples (i, j, k) such that ai + aj + ak ≥ X. There are T ≤ 50 test and each test includes number n ≤ 5000, X ≤ 1012 indicates the size of sequences, the key, respectively and n terms of sequence a1, a2, ..., an such that 1 ≤ ai ≤ 109, i = 1, 2, 3, ..., n. Example:

input:

2
5 300
100 100 100 100 100
5 301
100 100 100 100 100

output:

60
0

Problem 3.

Balanced number is a positive integer satisfied that: (1) The amount of even digit equals to the amount of odd digits. (2) The sum of even digits equals to the sum of odd digits. Ex: 1982, 11822989 are balanced numbers. Given L, R are two positive integer such that 1 ≤ L ≤ R ≤ 1012. Count the number of balanced numbers in the interval [L;R]. There are T ≤ 100 tests, each test includes 2 numbers L, R. Example:

input:

2
1 10000
45645 10987656

output:

450
29993

Problem 4.

Symmetric number is a positive integer greater than 9 and be unchanged when reading it from the left to right and from the right to left. Asymmetric number is a positive integer that not contain any symmetric number. Ex: 96276 , 1234 are asymmetric number. Given L, R such that 1 ≤ L ≤ R ≤ 1018. Count the number of asymmetric numbers in the interval [L;R]. There are T ≤ 100 tests, each test includes 2 numbers L, R. Example:

input:

2
123 321
123456789 987654321

output:

153
167386971
  • Vote: I like it
  • +9
  • Vote: I do not like it

»
11 years ago, # |
← Rev. 3   Vote: I like it +4 Vote: I do not like it

The second problem can be solved in O(n^2*logn). Sort the sequence. Then for every pair (i,j) find the index of the first element of the array which is greater than or equal to X-Ai-Aj (binary search), the k of triple (i,j,k) can be all elements which come after that element in the sorted array except i and j. so increase the answer by the corresponding number.

P.S. maybe we can achieve better complexity with two pointers method

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Thanks for your help! But in the contest, I also implemented this algorithm and got verdict TLE, another algorithm I tried (build an array sum of two terms of the given array and binary search on this) got the same result. I tried to improve the IO process a lot but it still didn't work, so I think it could be solved by harder techniques. I will consider two pointers method as you recommended.

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it +4 Vote: I do not like it

      Sorry, I didn't see that there are T<=50 tests.

      → Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

The first problem from CCC 2013 ( Canadian Computing Competition ) Day 2

Here is a link http://www.cemc.uwaterloo.ca/contests/computing/2013/Stage2/day2.pdf

But i could'nt find official solutions :(

→ Reply
»
11 years ago, # |
← Rev. 3   Vote: I like it +1 Vote: I do not like it

The Second problem...

You are looking for first element (i), second element will be j=i+1 and third element will be k=j+1. While(a[i]+a[j]+a[k]<=X) increase k. This is maximum sum for pair(i,j). Now add (k-j) to result. Increase j... While(a[i]+a[j]+a[k]>X) decrease k. And Add (k-j) to result again. Increase j again and look for third element (k) again etc... And do it for every first element (1<=i<=n-2).

At last answer = result*6 ( you know that why it is 6 ;) ) Time complexity will be O(N^2).

Sorry for my bad English. :)

→ Reply
  • »
    »
    11 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Maybe there is a better method like O(N*logN) or O(N*(logN)^2). I think solution is Segment Tree or Binary Search. "More power to your elbow !" :)

    → Reply
»
11 years ago, # |
  Vote: I like it +3 Vote: I do not like it

I believe that P3 is DP, like: dp[a][b][c][d] = count of numbers that starts with a, have length b, with (sum of odd digits-sum of even digits) c, (cnt of odd digits-cnt of even digits) d. But I don't have a clear idea yet.

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    1 ≤ L ≤ R ≤ 10^12 Did you see that?

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      not a big problem

      0<=a<=9 1<=b<=12 -120<c<120 -12<=d<=12

      using some tricks maybe we can generalize the query into different parts of elements in dp,sol should be in O((log L+log R)*log (R-L)) e.g.

      L=12 R=9801

      step 1: extract answer from 12-19

      equals dp[2..9][1][-1][-1]

      step 2: extract answer from 20-99

      equals dp[2..9][2][0][0]

      step 3: extract answer from 100-999

      equals dp[1..9][3][0][0]

      step 4: extract answer from 1000-8999

      equals dp[1..8][4][0][0]

      step 5: extract answer from 9000-9799

      equals dp[1..7][3][-9][-1]

      step 6: extract answer from 9800-9801

      equals dp[0..1][1][-1][-1]

      → Reply