→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3977 |
| 2 | tourist | 3815 |
| 3 | jqdai0815 | 3682 |
| 4 | ksun48 | 3614 |
| 5 | orzdevinwang | 3526 |
| 6 | ecnerwala | 3514 |
| 7 | Benq | 3483 |
| 8 | hos.lyric | 3381 |
| 9 | gamegame | 3374 |
| 10 | heuristica | 3358 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 170 |
| 2 | -is-this-fft- | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 160 |
| 5 | djm03178 | 157 |
| 5 | Dominater069 | 157 |
| 7 | adamant | 153 |
| 8 | luogu_official | 152 |
| 8 | awoo | 152 |
| 10 | TheScrasse | 147 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jan/05/2025 12:12:58 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











This problemset felt quite weird IMO.
Also, how does one get 100 on parks?
I discussed with tmw and it seems the following construction works:
Checkerboard all possible bench locations. On one color, draw a road directly above if possible, otherwise try to draw a road directly below it. On the other color, draw a road directly to the left if possible, otherwise try to draw a road directly to the right.
All solutions I've seen involve this tightening of the constraint by checkerboarding the grid of benches and then restricting one color to horizontal roads and one color to vertical roads. Why did you guys try this restriction? It seems nice to analyze I guess, but do you have any high-level intuition about why the problem is still solvable?
I can describe the thought process if it helps:
If you are given a set of roads, you can assign benches via matching (I actually used hopcroft karp with an essentially arbitrary spanning tree for 70). So it comes down to figuring out which arrangements of roads are good/bad.
Then I stumbled upon this configuration (excuse the quality):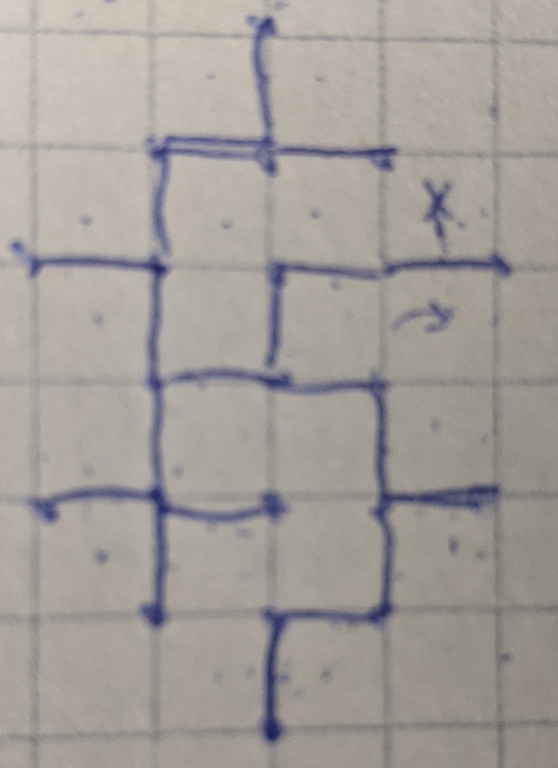
There are 20 possible bench locations and 20 roads. It fails though, because no matter what one of the 2 x's will be unused. So at most 19 benches will be used, which can't satisfy 20 roads' constraints.
So here, two things to notice:
1) An L-shape would perform better in that situation than a straight-line segment of length 2
2) A set of roads should allow for a "dense" arrangement of benches
Combining the two ideas, if you chain a bunch of L's together (to form diagonally jagged roads), you can place benches in basically every square along that diagonal, which is very space efficient.
If you look at how the diagonal road arrangement tiles the plane and arbitrarily choose that all horizontal roads have a bench below them, you get the bench checkerboard. If ever the diagonal formation breaks, the bench that would have continued the diagonal can be redirected to connect two adjacent diagonal strips. From here, it's just playing with the construction.
Bit of a tangent:
Speaking of Hopcroft-Karp/matching, we can rephrase this problem as a matroid intersection, where the ground set is road/bench pairs, one matriod is the partition matroid of benches (at most one per bench), and the other matroid is the graphic matroid over roads (no road cycles). We're just looking for any maximum matroid with size $$$N-1$$$.
General matroid intersection is pretty slow though, so I don't think this actually works for this problem.
Just a comment to the matching for 70 points: I did the bench-road matching as well, however, you don‘t need Hopcroft-Karp, because the roads will always have degree 2, and the benches always have degree at most 2 (for 70 points), so the graph actually consists only of chains and even cycles, where finding a matching is trivial.
For every pair of adjacent fountains, lets assign a bench that can take care of the road between them if it is built. Firstly, we split the coordinate plane into 2x2 grids and colour them with chessboard pattern. The center of each square is a candidate position of a bench, denoted with a pink cross in the figure. For each black square, we want the center to be responsible for the roads vertically above and below it, and for each white square, we want the center to be responsible for the roads left and right of it. That is, in the figure, we want each pink cross to take care of the two candidate roads that is touched by the pink line passing through it.
Now, lets solve subtask 5, where there are no 4 fountains forming a 2x2 square. We can consider all roads that we can possibly build, and if they dont form connected component we know answer is 0. Otherwise, lets find a spanning tree. Then, for each road that is in the tree, we will assign it to the bench that is responsible for it from the previous paragraph. Because there are no 2x2 squares, we know that each bench will only take care of at most 1 road and therefore we find a solution.
To get full solution, we want to stop considering some candidate roads so that:
1) Each bench is responsible for 1 candidate road only.
2) The fountains remain connected.
Lets consider all 2x2 squares where there is a fountain in all 4 corners. We will build dual graph, which is a graph with these 2x2 squares as vertices along with an additional vertex representing the outside region. Then, for each of these 2x2 squares $$$u$$$, there are two roads where the center is responsible for. If we walk through each of these edges, we will reach another vertex $$$v$$$. Lets build edge from $$$v$$$ to $$$u$$$.
Now, we will run a dfs from the outside vertex. It can be easily seen that we will reach all vertices, and thus we will get a dfs tree spanning all vertices. Now, we know that each edge in this spanning tree cuts a candidate road. Lets stop considering these roads that are cut. We can make such observations:
1) A spanning forest of fountains that belong to at least one 2x2 square remains. You can refer to the proof of $$$V-E+F=1+C$$$ to understand this. With this result we know that even after cutting, the connectivity of the graph doesnt change.
2) For each bench that are originally responsible for 2 candidate roads, we will cut at least one of them, because we need to pass through at least one of them to enter that 2x2 square.
Thus we can just continue with the new graph and plug solution for subtask 5 to finish the problem.
I will try to upload the problem to the gym. So if you want to test yourself, do not read them in advance.
Or not, cuz people were faster than me.
could you please give me the link on the gym for ioi 2021 day one problems ?
nvm, ignore
You can solve all problems here: https://oj.uz/problems/source/576
In case you want to solve it in 5 hours, you can try here: https://oj.uz/contest/view/IOI2021DAY1
Related post: https://mirror.codeforces.com/blog/entry/92088
is there scoreboard available ?
Yes, there is, see: https://mirror.codeforces.com/blog/entry/92067?#comment-807637
Oh i meant, scoreboard for the virtual contest published by oj.uz . Nvm they posted info here : https://mirror.codeforces.com/blog/entry/92088
If some node $$$i$$$ doesn't have an edge of type $$$r_i$$$ incident to it, the answer is trivial. Otherwise, for each node, take any of the edges of type $$$r_i$$$ incident to it and direct it out of this node. You'll get a functional graph. It's well-known that in such graph, each weakly connected component is a cycle with some trees "hanging" from it. Notice that all the nodes in any cycle can reach the same set of nodes, so we can compress each cycle into one node. After this step, each component will turn into a tree, but we still have more edges to consider. However, for now, only the root of any tree can have minimal reachability. So for each root, let's iterate over the edge going out of it. If we face an edge going to a node in this root's component, we close a new cycle, so we can compress it and so on. If we find an edge to a different component, we add it and stop iterating, since this node is not a root anymore. After this process is done, you'll get a bunch of trees such that the root of each tree doesn't have any more edges coming out of it, and only the roots can have minimal reachability (since the rest of the nodes reach the root AND themselves). So take the root(s) that have the minimal number of nodes compressed into them and you're done.
PS: in the implementation, you need to compress each cycle in a complexity proportional to its length to get a good amortized complexity.
You also need to be a little careful when iterating over the outedges from a root: you want to iterate only over the ones for which you have a valid key, you don't want to iterate over them multiple times, and you need to maintain those sets pretty efficiently. In order to do so, I believe you should maintain a BBST (std::set) of keys and a BBST of locked out-edges sorted by key-type for each compressed node, as well as a set/linked-list of unvisited unlocked outedges. Then, as you compress a cycle, you can merge smaller into bigger.
It looks similar to the efficient algorithm for Directed MST.
Btw, 17AC for P2 looks really overwhelming for me. I think the difficulty is nowhere near P1. Maybe I could solve it if I could imagine Directed MST algorithms, but I didn't (for obvious reasons). Anyone have good intuitions?
It seems the tests were weak, and that could be a part of explanation. But I don't know to which extent.
I think this was a lot of peoples' intuition:
Let's think about the first step. If someone has no out-edges with their own color, then they are the minimal sets. Otherwise, everyone has at least one outedge of their own color. Just pick one of these for each node, and you get a functional graph. Then, because reachability is transitive (if $$$a$$$ can reach $$$b$$$, and $$$b$$$ can reach $$$c$$$, then $$$a$$$ can reach $$$c$$$), we can contract the cycles of the functional graph and do it again.
Flushing this argument out and making it more bottom-up leads to final result.
You can solve the problems here:
Note that the statements (both English and Chinese) are not finished yet, will add them soon.
When encountering
Complication Error, try adding the Header file (e.g.#include "candies.h") in the front of your program.Does anyone have a solution for problem A?
Disregard, wrong problem oops --https://mirror.codeforces.com/blog/entry/92083?#comment-807698--
Oops disregard my earlier comment, that's problem C. For A (candies), there are 2 main ideas. The first is pretty simple: the operations are somewhat complicated, but we have all operations upfront, so we can "transpose" the problem. We'll maintain a segtree of updates indexed by time and we'll sweep through indices, answering one query at a time. As we sweep past $$$l[i]$$$ and $$$r[i]$$$, we will enable and disable the update at time $$$i$$$ in our segtree. This way, when we want to answer a query, we'll have all the updates available at once.
Thus, we just have to solve the $$$n=1$$$ version (in a way compatible with enabling/disabling on a segment tree). (This is pretty much subtask 4.) Here's an alternative view of updates. Think about the sequence of updates as a line graph, moving up-right or down-right, ignoring the lower and upper bounds, and think of the two bounds as horizontal walls. Then, if the line hits a wall, it pushes the walls along as it continues moving, and the answer is just where the line ends up relative to the walls. It's pretty easy to figure out where the line ends up (that's just the total of all updates), so we just want to figure out where the walls end up.
Now, let's think about the last time the line touches a wall. (We can force it to touch both walls at least once by adding dummy $$$v[-2] = +\infty$$$ and $$$v[-1] = -\infty$$$ updates, or we can just handle the case where it doesn't touch both walls as a special case.) WLOG, it touches the upper wall last, and let's say it's at time $$$t_u$$$ and height $$$h$$$. Then, after $$$t_u$$$, everything must stay within the interval $$$(h-c, h)$$$. Furthermore, it must touch the lower wall some time prior to it, and that last lower wall touch must be $$$\le h-c$$$, otherwise height $$$h$$$ won't be able to touch the upper wall. If we think about the last time $$$t_l$$$ where we're at height $$$h-c$$$, then between $$$t_l$$$ and $$$t_u$$$, everything must stay in $$$(h-c, h]$$$; we can't go below because $$$t_l$$$ is the last time at height $$$h-c$$$, and we can't go above because we're not allowed to do any more lower-wall-touches to bring the range back down. Thus, in the time range $$$(t_l, \infty)$$$, we stay within $$$(h-c, h]$$$ and hit $$$h$$$ exactly, so we can actually identify $$$t_l$$$ as the maximum time such that $$$\max_{t \in [t_l, \infty)} h(t) - \min_{t \in [t_l, \infty)} h(t) = c$$$, and then that interval is exactly where the walls end up (the answer is $$$h(\infty) - \min_{t \in [t_l, \infty)} h(t)$$$).
Thus, we just have to find this maximum time such that the suffix of the line graph has range $$$c$$$. Note that this $$$\max - \min$$$ range is increasing as we decrease $$$t_l$$$, because we're taking $$$\max$$$ and $$$\min$$$ of more elements. We can do this by binary searching on a segment tree of updates where we store maximum/minimum prefix sums (note that $$$h(t)$$$ is just a prefix sum of updates). This also easily supports enable/disable. The approach above assumes we can split a $$$v = +2$$$ update into two $$$v = +1$$$ updates, which is pretty easy to do implicitly.
This problem is somewhat similar to JOI 2021 Spring Camp foodcourt, and I'm pretty sure I've seen this exact touch-2-walls structure before in a different contest; maybe someone else remembers the problem.
This makes a lot of sense, very nice solution, thanks!
Problem A can also be solved on-line in time $$$O(Q \sqrt{N})$$$ using square root decomposition. We begin by "standardly" partitioning our array into blocks of size $$$\sqrt{N}$$$. Afterwards, each query will affect some blocks completely, and (at most 2) blocks partially. Let's bulk the operations for each of the blocks. We'll implement a procedure called
Commit(block)which will "commit" all updates.How to write this procedure?
Let's keep a function $$$f(x)$$$ where $$$f(x)$$$ is the final number of candies for an (initially empty) box with capacity $$$x$$$. This function looks like an increasing piecewise linear function, where slopes alternate between $$$0$$$ and $$$1$$$. We can update $$$f$$$ after a new operation by keeping track of the points where the slope changes in a stack.
Now, the least beautiful part about this approach is that computing function $$$f$$$ is not enough, because some boxes might have leftovers from earlier updates (they are not empty). But we can adapt it by noticing that the final number of candies for a box with capacity $$$c_i$$$ and $$$a_i$$$ initial candies is:
$$$a'_i = \max(0, \min(c_i - maxd, a_i) + mind) + f(c_i)$$$
Where $$$mind$$$ is the minimum delta over the current operations ($$$mind < 0$$$) and $$$maxd$$$ is the maximum delta. The reasoning is somewhere in the lines of:
"If $$$a_i + maxd > c_i$$$, then $$$a_i$$$ could have been $$$a_i - 1$$$ and the final answer wouldn't change. Also, if $$$a_i + mind < 0$$$, then $$$a_i$$$ could have been $$$0$$$ to begin with."
Unfortunately, the memory is also $$$O(Q \sqrt{N})$$$, which makes the solution risking both MLE and TLE, but after some little tinkering with the constant, it gets AC with 4s. The memory can be optimized to $$$O(Q + N)$$$ if you commit one block when there are more than $$$\sqrt{N}$$$ operations which affect it, though this was not necessary.
Source code: https://pastebin.com/HA7FJqaC
You can also solve it online in $$$O(Q \log^2(N))$$$ with $$$O(Q \log^2(N))$$$ memory: we just use a lazy-propagation segment tree, where the lazy tags are persistent treaps of the updates, and push-down is just treap merge. Queries involve just pushing lazy tags to the leaf, and then doing the same binary-search-on-treap as the offline solution. (This actually supports changing $$$c[i]$$$ as well.) I wonder if there's some segment-tree-beats or something to improve this complexity.
Wow, this is some next level voodoo (and, sadly, probably indistinguishable from $$$O(NQ)$$$).
[I think my proposed solution here was wrong, sorry about that]
By the way, the square root solution also supports updates of $$$c[i] \gets x$$$. ^_^
How to solve subtask 2 of Candies?
Note that the number of candies in each box will never decrease. That means that when the limit for one box is reached, it can't go higher. So we can calculate the number of candies in each box disregarding the limit constraint with prefix sums, and if $$$ans[i]$$$ is the number of candies in box $$$i$$$ in this case, we have $$$s[i] = \min(ans[i], c[i])$$$.
All queries are add. So just do offline range add with prefix sums.
Problem C, (Fountain Parks) is mine, really glad it made it into the contest! For anyone interested, here are some comments and history about the problem.
I came up with the problem in January 2020. A couple of days prior I had recieved a notebook for New Year's from a friend, and the layout of the pages was that they only had lattice points marked (as opposed to the ones I usually use with regular grids). I was trying to come up with problems in this notebook, and started drawing semicircles between some of the lattice points. Very quickly, an idea for a problem appeared in my head "Given a set of lattice points $$$S$$$, determine whether it is possible to draw some semicircles of unit diameter connecting pairs of points from $$$S$$$, so that no two of those semicircles intersect (or touch), and that the resulting graph is connected" (this is obviously the same problem).
It took me a while to solve, trying a lot of inductive approaches without much success. Finally, I stumbled across the checkerboard coloring idea mentioned in the solutions above (from a lot of examples I tried it seemed that some sort of "cyclic" assignment always works the best locally, so I tried to formulate this with a nice global condition), and managed to turn into a full solution fairly quickly. The solution I had in mind involves sorting the points by values of $$$x+y$$$ in decreasing order, and maintaining a forest of all connected currently components, with a bit of casework what happens when you add a new point.
Interestingly enough, at first I wanted to propose this at our national math olympiad (I was more of a MO than an OI competitor in my high school days) as "prove that if it's possible to connect the fountains in some way, it's also possible to connect and assign benches". However, I was not permitted to submit tasks for last year's national math olympiad, since I wasn't a member of the comittee, which made me rethink about where to send the task. Then I realized that my solution is pretty (completely) algorithmic in nature and that it would make for a nice informatics problem, and decided I would try to submit it for IOI 2021.
Like with most problems (especially construction problems), I tried to be careful that I'm not missing anything obvious. What made me convince myself that this problem is most likely not trivial is the fact that I found a large family of sets of fountain positions of size $$$N$$$ that have exactly $$$N-1$$$ places where you can put the bench (meaning that its $$$2\times2$$$ has at least two fountains), meaning that you have to be quite careful how you assign benches for these configurations. Try and figure out some configurations like this, I find the construction cute.
I hope you enjoyed the problem, and congratulations to everyone who solved it!
I wonder who that friend is...
Nice that two Serbian tasks were on the same day of IOI, who knew IOI day 1 would be Serbian Olympiad in Informatics Open Contest :)
really exciting to see how OM problems can be used in OI and vice versa. A few days ago I saw a comment about IMO'19 Problem 5 being used for a recent OpenCup Contest.
what‘s rainboy’s name?
Rain Jiang
Problem 2. Keys:
My solution is identical to JOI Open 2019 T3. Virus Experiment.
Consider Borůvka's algorithm (the key ideas): if you can reduce the number of candidate nodes to half in 1 round, after $$$\log_2 n$$$ rounds you can just calculate the answer with a brute-force BFS.
Can anyone tell me how to solve problem A : candies sub3 and sub4 ?
anyone ?
I wonder the same thing
Yes, that's strange. IOI happened almost 9 months ago and there isn't any official editorial yet :(
I think here is sample code. I had a quick look, isn't it based on full mark solution?
Yes it is
For sub3 use Segment Tree Beats
In sub4, if we sort array C, then after each query each element of some prefix will be set either to zero or to its max value(C[i]), and all other elements will be increased by v. For that, we can maintain a lazy segtree with range updates(set some segment to 0, set some segment to max value, add some value to a segment) and find the prefix for queries with binary search. Code: link
What could be the problem with this code for subtask 2 in A?
I think that you should use long long int
Thank you for your kindness replying, but it doesn't work either. In the condition it says the returned vector must be int. I've also tried this but I got wa in all cases.
You should keep variable long long int sum=0.In each step from 0,1... to n-1 sum=sum+pre(i).And answer for each i is minimum of sum in that step and c(i).
The previous commenter was right — the problem lies in the line
ans[i] = min(ans[i-1]+pre[i], 1LL*c[i]);Because $$$\text{ans}[i]$$$ is bounded above by $$$\text{c}[i]$$$, it's possible that $$$\text{ans}[i] \neq \text{pre}[0] + \text{pre}[1] + \cdots + \text{pre}[i]$$$.
For example, consider the case $$$n = 3$$$, $$$c = [5, 10, 15]$$$, and the query $$$l = 0, r = 1, v = 12$$$. Then $$$\text{ans}[2] = \min(\text{ans}[1] + \text{pre}[2], \text{c}[2]) = \min(10 - 12, 15) = -2$$$, which isn't true. You could fix it by keeping a sum variable, as EJOI_Gold said, or by precalculating the values of $$$\text{pre}[0] + \text{pre}[1] + \cdots + \text{pre}[i]$$$.