Доброго времени суток! Подскажите, пожалуйста, куда можно сдать пересечение полуплоскостей в 2D.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
4 дня
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
4 дня
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 166 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 19.11.2024 17:51:23 (l1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










1520
Мне одному не очевидно, как здесь использовать пересечение полуплоскостей?
ну диаграмма вороного. или ты намекаешь, что там всё проще?
Ну, там точно все проще. Нас интересуют центры описанных вокруг каждой тройки окружностей и точки на внешней окружности. Первые просто находятся (или только радиусы), вторые бинпоиском по ответу обрабатываются. Задачу не сдавал. Диаграмма вороного немного нужна, если хочется квадрат. Но откуда пересечение полуплоскостей?
Ага, понял, можно вороного через пересечение полуплоскостей, совсем втупую — O(n4), что долго. Наверно каким нибудь "заворачиванием подарка", можно соптимайзить до O(n3), что уже норм.
Не, казалось бы, хаворачивание подарка дает квадрат, а куб — это просто перебрали тройку точек и узнали радиус описанной вокруг них окружности. Для внешнего круга можно n log ans. Разве нет?
За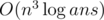 я умею без всяких вороновых, но немного не так как ты говоришь. Мне интересно как можно пересекая полуплоскости построить вороного за O(n2)? Как это сделать совсем втупую: фиксируем точку, строим O(n) срединных перпендикуляров между нашей точкой и всеми остальными, всех их пересекаем, получаем O(n2) точек, далее за O(n) проверяем каждую точку на принадлежность каждой полуплоскости — профит за O(n3) построили ячейку вороного. Как построить ячейку за O(n)? (P.S. ни диаграмму вороного, ни пересечение полуплоскостей ни разу не писал, мне не понятно как пересечь n полуплоскостей за O(n))
я умею без всяких вороновых, но немного не так как ты говоришь. Мне интересно как можно пересекая полуплоскости построить вороного за O(n2)? Как это сделать совсем втупую: фиксируем точку, строим O(n) срединных перпендикуляров между нашей точкой и всеми остальными, всех их пересекаем, получаем O(n2) точек, далее за O(n) проверяем каждую точку на принадлежность каждой полуплоскости — профит за O(n3) построили ячейку вороного. Как построить ячейку за O(n)? (P.S. ни диаграмму вороного, ни пересечение полуплоскостей ни разу не писал, мне не понятно как пересечь n полуплоскостей за O(n))
Ну,конкретнов этой задаче не нужно строить ячейку,просто проверяем ключевые точки.Ячейкувороного просто строить за квадрат. Просто каждый серпер пересекаем с остальными и, в зависимости от относительного наклона прямых находим луч пересечения данного серпера с полуплоскостью, образованнойдругим. Пересекли все эти лучи — получили отрезок на внешней границе ячейки. Так за квадрат для каждой ячейки можно построить диаграмму. Про линию для каждой ячейки сходу не расскажу, там что-то в духе алгоритма дляпостроения выпуклой оболочки.
Если что, то всё что читал (но не писал), это nlogn через skanline, nlogn через bst, и n2logn с помощью сортировки и стека. Даже последний не слишком простой.
Вроде смотря как реализовать, казалось бы за четвёртую, но летает, прошло за 0.031. Пытался в своё время худший случай построить, вообще выходила сложность кажется n^3 или n^4/bigconst.
Волшебный лес
http://acm.timus.ru/problem.aspx?space=1&num=1062
Но тут, на мой взгляд, не совсем тривиально, что к 2D сводится.
NEERC 2010, задача J.