359A - Таблица
Давайте рассмотрим все ячейки, которые расположены в первой строке. Очевидно, что если хотя бы одна из них хорошая, то ответ равен двум. Аналогично, если хорошая ячейка расположена в первом столбце, либо в последней строчке или в последнем столбце, ответ также два. Иначе, ответ равен четырем.
Авторское решение: 4968279
359B - Перестановка
Ответом будет являться немного изменненая перестановка 1, 2, ..., 2n. Для каждого 1 ≤ i ≤ k поменяем местами числа 2i - 1 и 2i. Не трудно проверить, такая перестановка будет хорошей.
Авторское решение: 4968385
359C - Простое число
Очевидно, что ответ это xv. Пусть sum = a1 + a2 + ... + an. Тогда рассмотрим все числа вида si = sum - ai. Тогда, чтобы узнать, чему равно v мы поступим так: Рассмотрим систему счисления по основанию x, где si — разряд. Тогда, когда мы выполним все переносы по степеням, нужно найти минимальный разряд, в котором стоит не ноль. Тогда v будет равно именно этому разряду. Чтобы выполнить переносы, можно было бы поступить так. Рассмотрим последовательность степеней как убывающую последовательность. Теперь будем выполнять следующее "пока можно". Возьмем минимальную степень v, посчитаем количество слагаемых cnt, которые имеют такую же степень. Если cnt кратно x, тогда мы их заменим cnt / x слагаемых вида v + 1. Поскольку последовательность степеней была убывающей, мы можем просто приписать их в конец. Если же cnt не кратно x, тогда мы нашли нужную минимальную степень v. Также стоит не забывать, что v = min(v, sum).
Авторское решение: 4968346
359D - Пара чисел
Достаточно очевидное замечание: если пара (l, r) удовлетворяет условию 1, тогда min(l, r) = НОД(l, r). Где min(l, r) — минимум на подотрезке (l, r). Аналогично, НОД(l, r) — НОД всех чисел на подотрезке (l, r). Посчитаем структуру данных, которая позволит нам быстро отвечать на запросы минимума на отрезке и НОД на отрезке, например за O(1). Это можно достичь используя структуру данных Sparce Table. Конечно, на запрос НОД(l, r) мы не сможем отвечать за O(1), однако будет достаточно быстро работать. Также стоит отметить, что решение, которое использует дерево отрезков, очень вероятно получит TL. Воспользуемся бинарным поиском для того, чтобы найти максимальное возможное значение r - l:
lf = 0; //левая граница поиска
rg = n; //правая граница поиска
while (rg - lf > 1) {
int mid = (lf + rg) / 2;
if (ok(mid)) //ok(mid)
lf = mid;
else
rg = mid;
}
ok(mid) — функция, которая определяет, существует ли отрезок который удовлетворяет условию min(l, r) = НОД(l, r) и mid = r - l. Если таковой есть, то обновим границы бинпоиска. После того, когда мы узнаем величину r - l восстановить ответ не составит труда.
Здесь есть информация про Sparce Table
Авторское решение: 4968587
359E - Порядок
Запустим рекурсивную функцию, которая включит свет во всех комнатах, где это возможно. Кроме того, она посетит все комнаты, среди тех, которые возможно посетить. Пусть эта функция называется paint(x, y), где x, y — текущая комната. Эта функция будет работать так: Посмотрим во все 4 направления. Если в заданном направлении идти можно по правилу 3 из условия, и клетка (nx, ny) еще не посещена, рекурсивно пойдем именно в эту клетку. Кроме этого, будем включать свет везде, где можно. Если мы не посетили нашей функцией некоторую клетку, где есть свет, то ответ NO. Иначе ответ есть. Далее с помощью обхода в ширину посчитаем для каждой комнаты, в которой включен свет, расстояние от старта, причем разрешается ходить только по тем комнатам, где свет горит. Пусть для комнаты (x, y) это значение равно dist(x, y). Теперь запустим похожую рекурсивную функцию, которая будет выключать свет. Эта функция будет работать так: Посмотрим во все 4 направления. Если в заданном направлении в комнате (nx, ny) еще горит свет, а dist(nx, ny) > dist(x, y), то запустим нашу функцию рекурсивно от (nx, ny), а потом вернемся в текущую комнату. Если такой соседней клетки нет, выключим свет. Более подробно детали можно изучить в моем решении.
Авторское решение: 4968657











А можно по подробней разборы для див. 2? я до написанного по задаче С сам додумался, а как реализовать учитывая, что степень могут быть 10^9 я так и не разобрался до конца
Спасибо за оперативность! :)
У D есть решение за линейную память и ту же сложность: Для каждого индекса i посчитаем величины l[i] и r[i] означающие соответственно 'какой индекс первого числа лежащего слева(справа) от i такого, что он уже не делиться на a[i]'. Считать это быстро можно 'прыжками': пусть изначально l[i] = i — 1, тогда если a[l[i]] % a[i] != 0 то мы уже узнали значение l[i], иначе положим l[i] := l[l[i]]. Это верно т.к. если a[l[i]] делиться на a[i] то a[i] делит также все числа, что делит a[l[i]]. Таким образом можно для каждого индекса i найти максимальные по включению границы l[i], r[i] и получить ответ.
Когда во время контеста я увидел подобное решение, у меня сразу возникла аналогия с dsu и префикс-функцией. Спасибо за разъяснения.
Если прыжки делать очень плохо то мы должны наткнутся на ТЛ. однако этого не происходит.
я делаю прыжок только для левого и правого соседа если могу.
Но такое решение валится на тесте (1 2 1 2 1 2 ... и так далее 300000 раз)
Плз. помимо разбора делайте тесты сильнее. Посылка: 4990277
вы делаете прыжок очень медленно, надо типа такого:
такой прыжок проходит ваш тест
В задаче Е многие (и я в частности) сдавали просто рекурсивный paint(x, y) который не только зажигал где возможно свет, но и в конце рекурсивного вызова его гасил.
For problem D, I don't understand why this (4969570) simple solution passed the time limit, it's run in O(n^2) right? And why it passed the worst case (test case #23) just in 46ms! Unbelievable :-O
Correct me if I'm wrong
Notice the operation
r =i+1. It should be O(N2) theoretically, but it's near impossible to make test data that cause it to fail (for example, ai = 2N - i is a case where it performs at least N2 operations).It's not O(N^2), it's O(N*log(Range)) in worst case, in average way faster than original solution. The worst case would be when in every iteration we go far to the left, but just one step right. But for this to happen, consecutive numbers should be divisors of their predecessors, example:
32 16 8 4 2 1
In every iteration we make only one step right(by increasing i), but many steps left. However the input range (1..10^6) limits max steps to the left to log(10^6)=20
Ok, I didn't read you already gave the worst case scenario. But still, N is not the only parameter of algorithm complexity, range is also such. So, if range was infinite, it would be O(N^2), but since it's limited, I would say it is O(N*log(Range)).
Well, actually there are many other ways to solve this problem, my solution uses maps only and the worst time is O(n * (greatest number of divisors for any number))
i.e: 6 has 4 divisors (1, 2, 3, 6)
5605391
Any other explanation for D ?
My solution is a bit different used a stack left , a stack right. You'll push a[i] if stack.top() % a[i] != 0 else stack.pop(); you'll find the farthest element which is divisible by a[i]. 4966411
great solution , I share the same idea with you in the first place but i can't find the way how to caculate L[i] and R[i] . Now I know it could be solve by using stack . Tks a lot :D
meodorewan Can you please explain a little bit. I have been trying to look up some solution that does not use a sparse table. Yours seems the best. I tried to understand your code, but it'd be of great help if you could please explain this solution of yours.
Скажите, пожалуйста, почему в задаче С нельзя идти с переносом не в порядке убывания, а в порядке возрастания?
Ну или если можно, то почему тогда такое решение не проходит?
4972169
UPD: Все понял, я не проверял, что ответ может быть больше, чем сумма.
I do not fully understand the solution to D. I have understood till the part where we need to have a data structure which gets GCD(l, r) and min(l, r) in a short time.
Say I use a segment tree for that. Now what? Binary search how? Can someone kindly explain?
for each element i we search for biggest j such that each element in range i...j is divisible by element i , also we search for smallest k such that each element in range k...i is divisible by element i so we have k ... j is maximal good range , we do this for each i
So we basically need only data structure for GCD(l, r) right? No need of min(l, r) then.
Find the largest 'j' such that GCD(i, j) = a[i] and find smallest 'k' such that GCD(k, i) = a[i].
Yes
We want to find the maximum possible length of a segment such that there exists a segment that satisfies both conditions and has this length.
It's obvious that this F(len) = {1 if such segment exists and 0 otherwise } is monotonous so we use binary search.
Now for each of our guesses (for each of mid in bin search) we need to calc F(mid).
We iterate through each segment of length mid and if GCD of all numbers on current segment is equal to minimum of all numbers on the segment then we've just found a satisfying segment (F(mid) = 1). And if we haven't found any then F(mid) = 0.
This is exactly the way described in the blog but a lot more clearer. Now I understand this method. Thank you :)
EDIT : Just tried this method using two segment trees. One for GCD(i, j) and the other for min(i, j). Still getting TLE. What is the reason? Segment tree is slow?
My submission : http://mirror.codeforces.com/contest/359/submission/4980867
EDIT 2: Replaced segment tree with sparse table and AC now. Learnt something new :)
I think you have to pre-compute segments by using sparse table which is <O(nlgn),O(1)>. There is a link in tutorial about it.
For D, there is a much easier and faster solution. For each direction(left to right or right to left) see how much you can go with one number. if your number is not divisible any more try to continue it by your current value. The only problem is same number's left and right interval may intersect. Mine: 4974772
I still cannot understand the solution described for problem C. It would be very much appreciated if someone could please explain. Thanks!!
I dont understand author's solution too. I have next solution (it maybe like authors):
at first there is next fraction: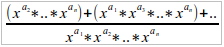
then lets find [max a] — in my example it is a^n
at numerator we can factor out minumum of numerator. it is (without [max a] — at my example [max a] is a^n) or ([sum of a-elements] — [max a]), so then in brackets:
(without [max a] — at my example [max a] is a^n) or ([sum of a-elements] — [max a]), so then in brackets: 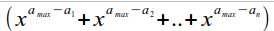
so now the answear is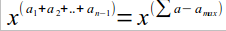
then sum in brackets maybe have addition common divisor for x. For example: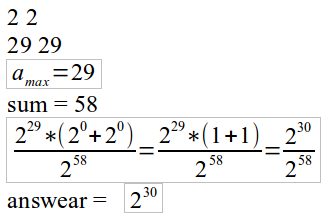
for finding addition common divisor I do next: count different degrees at brackets. and go from degree 0 and try convert count degree of 0 to count degree of 1 and continue. I check that count of degree mod x == 0 and stop if its not so. when stop i can add to answear degree on what i stop. for example: on example stopping on degree 2, so to answear i can add 2. my solution:4986617
on example stopping on degree 2, so to answear i can add 2. my solution:4986617
Thanks mate..
Best codeforces set I have ever participated. The problems were really very interesting with an excellent statement and samples. super like to the authors \m/
В задаче C — Простое число, почему ответ всегда x в степени v. На тест
4 6
1 1 2 2
у авторcкого решения ответ — 1024. Разве не 2058?
UPD. Не заметил, x — простое число
in problem E whats the logic behind calculating distance form bfs and using it in repaint
In worst case we will visit only 500*500 cells and 4*500*500 actions needed . Simple dfs is enough . Here's my ac code
The problem D can be solved with a complexity O(n). http://mirror.codeforces.com/contest/359/submission/5035770
In solution of problem C. I don't understand why we should do v = min(v, sum). is v really can be higher than sum?
For problem D, i got ac with tutorial solution. But now i am confused about the complexity. isn't it n*logn*logn*logn? How come it still passed with sparse table but when tried with segment tree, it didn't? Please correct me if i am wrong.
Can anyone explain problem C?
In problem D, why is segment tree slower than sparse table?
Time complexity of segment tree: Build-O(n) and Query-O(logn)
Time complexity of sparse table: Build-O(nlogn) and Query-O(logn)
So, looking at this 2 complexities, isn't segment tree supposed to be faster than sparse table?
query is O(1) in a sparse table.
For problem D, use Left Right for a much easier method :v Link: https://mirror.codeforces.com/contest/359/submission/105036790