Для понимания этой статьи необходимо знать базовое ДО и желательно понимать, как работает обычное 2D ДО.
Решим следующую задачу:
Дана таблица $$$n \cdot m$$$, поступают 2 вида запросов:
1) Прибавить $$$x$$$ на прямоугольнике $$$[l1, r1], [l2, r2]$$$.
2) Посчитать сумму на прямоугольнике $$$[l1, r1], [l2, r2]$$$.
Почему нельзя использовать пуши? Для массовых операций с пушами должно быть выполнено свойство, что отложенная операция может складываться, но в случае 2D ДО мы должны складывать не числа, а отрезки, и их объединять уже не получится. Но помимо пушей есть другой тип массовых операций.
Сперва научимся делать прибавление на отрезке и сумму на отрезке без пушей в одномерном ДО.
В каждой вершине будем хранить $$$sum[v]$$$ и $$$add[v]$$$ — сумму на отрезке и сколько мы прибавим каждому элементу на отрезке. Рассмотрим запрос прибавления: для всех вершин, посещенных нашей функцией (на картинке желтые и зелёные), мы корректно пересчитаем значение в вершине, для суммы это $$$sum[v] += (min(r, rx)-max(l, lx)) \cdot x$$$, но сумма в вершинах ниже останется старой (красные). Чтобы это учесть, в тех вершинах, в которых остановилась функция (зелёные) сделаем $$$add[v] += x$$$. 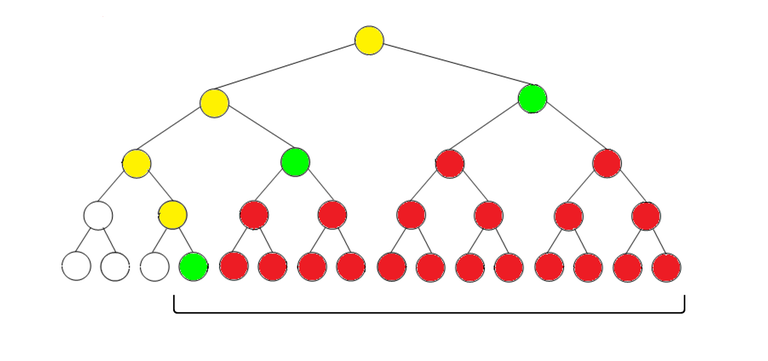
Номер корня равен 0, реализация на полуинтервалах
void upd(int l, int r, int lx, int rx, int v, int x) {
if (l >= rx || r <= lx) return;
sum[v] += (min(r, rx)-max(l, lx)) * x;
if (l >= lx && r <= rx) {
add[v] += x;
return;
}
int m = (l + r) / 2;
upd(l, m, lx, rx, v+1, x);
upd(m, r, lx, rx, v+(m-l)*2, x);
}
Теперь запрос суммы. Чтобы узнать актуальную сумму в вершине, нужно взять сумму $$$add[p]$$$ по всем предкам, умноженную на длину отрезка, и $$$sum[v]$$$. Чтобы лучше понять, почему это так, попробуйте посчитать сумму для красной вершины на картинке. Функция запроса будет такой же, как и в обычном ДО, только нужно поддерживать сумму на пути от корня до вершины.
В реализации можно даже не поддерживать сумму на пути, а просто когда мы спускаемся добавлять к ответу $$$add[v] \cdot (min(r, rx)-max(l, lx))$$$, это равносильно тому, что описано выше. Позже именно такой способ будет использоваться для больших размерностей.
int ask(int l, int r, int lx, int rx, int v) {
if (l >= rx || r <= lx) return 0;
if (l >= lx && r <= rx) {
return sum[v];
}
int m = (l + r) / 2;
return ask(l, m, lx, rx, v+1) + ask(m, r, lx, rx, v+(m-l)*2) + (min(r, rx)-max(l, lx)) * add[v];
}
Теперь этот же способ можно использовать для двумерного ДО.
Сделаем ДО по первой координате. В вершине, отвечающей за отрезок $$$[x1,x2]$$$ будет массив, отвечающий за прямоугольник $$$[x1, x2], [0, m-1]$$$, где j-тый элемент равен $$$\displaystyle\sum_{i = x1...x2} mas[i][j]$$$, в частности, в листах ДО будут просто строки таблицы, а в корне будет массив сумм столбцов (посмотрите на рисунок для лучшего понимания). На этих массивах в каждой вершине делаем ДО $$$sum[v]$$$ и изначально заполненный нулями $$$add[v]$$$.
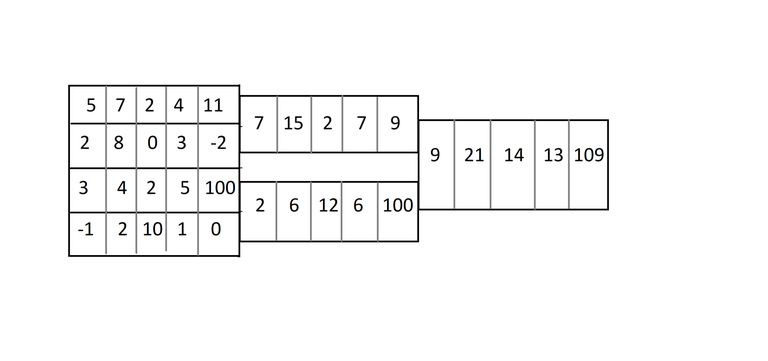
Sorry for my bad Paint
Выглядеть запрос прибавления будет так же, как и в одномерном случае: корректно пересчитываем $$$sum[v]$$$ для всех посещенных вершин, для этого прибавим на отрезке $$$sum[v][l2...r2] += x \cdot (min(rx, r1) - max(lx, l1))$$$. В вершинах, где остановилась функция, запомним, что для всех вершин ниже текущей для второй координаты нужно прибавить $$$x$$$ на отрезке $$$[l2, r2]$$$.
void upd(int l1, int r1, int lx, int rx, int l2, int r2, int v, int x) {
if (l1 >= rx || r1 <= lx) return;
sum[v].upd(l2, r2, x * (min(rx, r1) - max(lx, l1)));
if (l1 >= lx && r1 <= rx) {
add[v].upd(l2, r2, x);
return;
}
int med = (l1 + r1) / 2;
upd(l1, med, lx, rx, l2, r2, v+1, x);
upd(med, r1, lx, rx, l2, r2, v+(med-l1)*2, x);
}
Запрос суммы тоже не будет отличаться от одномерного случая: в конечных вершинах прибавляем к ответу $$$\sum sum[v][l2...r2]$$$, и спускаясь по ДО прибавляем к ответу $$$\sum add[v][l2...r2] \cdot (min(rx, r1) - max(lx, l1))$$$.
int ask(int l1, int r1, int lx, int rx, int l2, int r2, int v) {
if (l1 >= rx || r1 <= lx) return 0;
if (l1 >= lx && r1 <= rx) {
return sum[v].ask(l2, r2);
}
int med = (l1 + r1) / 2;
return ask(l1, med, lx, rx, l2, r2, v+1) + ask(med, r1, lx, rx, l2, r2, v+(med-l1)*2)
+ add[v].ask(l2, r2) * (min(rx, r1) - max(lx, l1));
}
Можно заметить, что код практически не отличается от одномерного случая, на самом деле можно обобщить этот способ для k-мерного ДО, так как для этого нужно будет иметь k-1-мерное ДО. Однако на каждом слое создаётся 2 массива размера 2n, итого памяти будет $$$O(4^k \cdot n)$$$ и один запрос $$$O(\log^k n)$$$.
Что делать, если в задаче координаты до $$$10^9$$$? Разумеется можно сделать оба ДО неявными, но в таком случае потребление памяти станет неприлично большим, так что лучше сжать по первой координате, а по второй сделать неявное ДО, или же можно хитро сжать координаты отдельно для значений на отрезках каждой вершины, тогда память будет $$$O(n \cdot \log n)$$$.
Насколько в целом эта техника применима? Например таким ДО можно было сдать в лоб задачу A3 недавно прошедшего отбора tinkoff generation, но в целом техника довольно специфическая, хотя пару раз была полезна и в одномерном ДО неплохо ускоряет "сумма на отрезке и прибавить на отрезке"(у меня ~2 раза быстрее способа с отложенными операциями).
Вот полный код 2D ДО: https://pastebin.com/aWesKi0a










