Задачи A и B не представляли идейной сложности, поэтому начнем сразу с C.
Задача C
Положим β = α / 10. Тогда заданные числа - это a1 = [β], a2 = [2β], a3 = [3β], ... an = [nβ] и нужно определить [(n + 1)β] ([x] - целая часть числа). Данные равенства эквивалентны системе неравеств: an ≤ nβ < an + 1,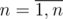 . Выбирая максимум по левым частям и минимум по правым, получим неравество вида A ≤ n < B. Теперь осталось сравнить целую часть числа A / (n + 1) и B / (n + 1). В случае если B поделилось нацело, нужно вычесть из правой части единичку, т.к. справа неравенство строгое.
. Выбирая максимум по левым частям и минимум по правым, получим неравество вида A ≤ n < B. Теперь осталось сравнить целую часть числа A / (n + 1) и B / (n + 1). В случае если B поделилось нацело, нужно вычесть из правой части единичку, т.к. справа неравенство строгое.
Задача D
Создадим векторы vi, в первый из которых v1 будем складывать позиции единичек, в v2 - двоек, в v3 - троек, и т.д. Их можно заполнить за один проход по данной последовательности. Количество перестановок - это количество единичек, или размер первого вектора. Мысленно определим первую единичку в первую перестановку, вторую - во вторую и т.д. Теперь перейдем к двойкам. Если их больше, чем единичек - решения нет. Иначе определим первую двойку в первую перестановку, вторую - во вторую и т.д. Возможно, несколько последних перестановок останутся без двоек. Дальше рассуждаем также для троек (которых должно быть не меньше, чем двоек) и т.д. Получаем решение за O(n).
Задача E
Расскажу два решения. Первое решение разбирает отдельно три возможных случая. Построим граф, вершинами которого являются пары (h, t) - текущие количества голов и хвостов у Змея Горыныча. Ребра определяются возможными ударами Иванушки. Сначала при помощи обхода в ширину определим, можно ли из стартового состояния добраться до (0, 0) и за сколько шагов. Затем проверим, возможна ли ничья. Она возможна, если в графе есть циклы. Иначе граф ациклический и при помощи динамики на ациклическом графе можно определить самый длинный путь до состояния победы Змея.
Второе решение - реализовать алгоритм, который часто пишут для игр на циклических графах. По сути описанный процесс и является игрой на циклическом графе, только ходы Горыныча детерминированы. Начнем с тех состояний, для которых мы знаем ответ, т.е. (0, 0) и h + t >= R, и будем двигаться от них в обратном направлении по ребрам, помечая остальные состояния выигрышнsми или проигрышными. Непомеченные состояния останутся ничейными.
Задача F
Для каждого из n дней необходимо решать так называемую "непрерывную задачу о рюкзаке". Она решается жадно: отсортируем фирмы по цене производимого ими снега и будем брать снег с минимальной цене, пока не наберем нужный объем. Решение с сортировкой при каждом n не проходило по времени. Авторское решение работает за O(nm) и основано на идеях быстрой сортировки (QuickSort). Выберем случайный элемент r на имеющемся отрезке. Как в QuickSort, переупорядочим остальные элементы, чтобы элементы, меньшие r, шли раньше него, и элементы, большие r - позже. Посчитаем суммарный объем снега с ценами, меньшими r. Если его достаточно - решаем задачу на левом подотрезке. Если нет - покупаем весь левый подотрезок и рекурсивно переходим к правому.
Отмечу еще одну неприятную особенность этой задачи. С одной стороны, ответ может быть достаточно большим. С другой стороны, требуется большая точность. Поэтому нужно вычислять целую и дробную части ответа отдельно.
Задача C
Положим β = α / 10. Тогда заданные числа - это a1 = [β], a2 = [2β], a3 = [3β], ... an = [nβ] и нужно определить [(n + 1)β] ([x] - целая часть числа). Данные равенства эквивалентны системе неравеств: an ≤ nβ < an + 1,
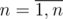 . Выбирая максимум по левым частям и минимум по правым, получим неравество вида A ≤ n < B. Теперь осталось сравнить целую часть числа A / (n + 1) и B / (n + 1). В случае если B поделилось нацело, нужно вычесть из правой части единичку, т.к. справа неравенство строгое.
. Выбирая максимум по левым частям и минимум по правым, получим неравество вида A ≤ n < B. Теперь осталось сравнить целую часть числа A / (n + 1) и B / (n + 1). В случае если B поделилось нацело, нужно вычесть из правой части единичку, т.к. справа неравенство строгое.Задача D
Создадим векторы vi, в первый из которых v1 будем складывать позиции единичек, в v2 - двоек, в v3 - троек, и т.д. Их можно заполнить за один проход по данной последовательности. Количество перестановок - это количество единичек, или размер первого вектора. Мысленно определим первую единичку в первую перестановку, вторую - во вторую и т.д. Теперь перейдем к двойкам. Если их больше, чем единичек - решения нет. Иначе определим первую двойку в первую перестановку, вторую - во вторую и т.д. Возможно, несколько последних перестановок останутся без двоек. Дальше рассуждаем также для троек (которых должно быть не меньше, чем двоек) и т.д. Получаем решение за O(n).
Задача E
Расскажу два решения. Первое решение разбирает отдельно три возможных случая. Построим граф, вершинами которого являются пары (h, t) - текущие количества голов и хвостов у Змея Горыныча. Ребра определяются возможными ударами Иванушки. Сначала при помощи обхода в ширину определим, можно ли из стартового состояния добраться до (0, 0) и за сколько шагов. Затем проверим, возможна ли ничья. Она возможна, если в графе есть циклы. Иначе граф ациклический и при помощи динамики на ациклическом графе можно определить самый длинный путь до состояния победы Змея.
Второе решение - реализовать алгоритм, который часто пишут для игр на циклических графах. По сути описанный процесс и является игрой на циклическом графе, только ходы Горыныча детерминированы. Начнем с тех состояний, для которых мы знаем ответ, т.е. (0, 0) и h + t >= R, и будем двигаться от них в обратном направлении по ребрам, помечая остальные состояния выигрышнsми или проигрышными. Непомеченные состояния останутся ничейными.
Задача F
Для каждого из n дней необходимо решать так называемую "непрерывную задачу о рюкзаке". Она решается жадно: отсортируем фирмы по цене производимого ими снега и будем брать снег с минимальной цене, пока не наберем нужный объем. Решение с сортировкой при каждом n не проходило по времени. Авторское решение работает за O(nm) и основано на идеях быстрой сортировки (QuickSort). Выберем случайный элемент r на имеющемся отрезке. Как в QuickSort, переупорядочим остальные элементы, чтобы элементы, меньшие r, шли раньше него, и элементы, большие r - позже. Посчитаем суммарный объем снега с ценами, меньшими r. Если его достаточно - решаем задачу на левом подотрезке. Если нет - покупаем весь левый подотрезок и рекурсивно переходим к правому.
Отмечу еще одну неприятную особенность этой задачи. С одной стороны, ответ может быть достаточно большим. С другой стороны, требуется большая точность. Поэтому нужно вычислять целую и дробную части ответа отдельно.
Задача G
Заданный граф представляет собой связный граф с одним циклом. Сначала научимся решать задачу для дерева. Подвесим дерево за произвольную вершину и стандартной динамикой вычислим для каждого поддерева
1) количество вершин в нем;
2) сумму расстояний от корня до всех вершин поддерева.
После этого мы получим ответ на задачу для корня. Чтобы определить ответ для остальных вершин, совершим еще один обход по дереву. Рассмотрим переход от вершины u к ее потомку v. Чтобы добраться до v из вершни ее поддерева, нужно будет проделать тот же путь, что и до u, только не проходя последнее ребро. Наоборот, для всех остальных вершин путь увеличится на длину этого ребра. Таким образом, d[v] = d[u] - L(u, v) * c[v] + L(u, v) * (n - c[v]), где c[v] - количество вершин в поддереве с вершиной v.
Теперь перейдем к графу с одним циклом, к которому возможно крепятся деревья. Корнями деревьев будем считать вершины цикла. Посчитаем ответ внутри каждого дерева. Общий же ответ складывается для каждой вершины из:
1) суммы длин путей внутри ее дерева;
2) суммы для всех остальных деревьев путей от их корней до всех вершин в дереве (потому что чтобы добраться до некоторой вершины из другого дерева, нужно пройти через его корень);
3) длины пути от вершины до корня ее дерева, умноженной на общее количество вершин в других поддеревьях;
4) сумма вида <длина кратчайшего пути по циклу от корня до дерева t> * <количество вершин в дереве t>.
Наиболее трудным является вычисление слагаемого 4. Для его подсчета нужно пройти по циклу двумя указателями: на текущую вершину и на вершину в цикле, которая разделяет вершины, от которых надо идти вправо и от которых надо идти влево до текущей вершины. Двигая указатели, можно за суммарное линейное время пересчитывать частичные суммы, необходимые для получения слагаемого 4.
Задача H
Представим сначала, что у нас ровно m черно-белых плиток. Тогда можно поступить следующим образом. Будем перебирать клетки по порядку сверху-вниз слева-направо. Сначала положим a черны плиток, потом - c = m черно-белых, затем - b белых. В итоге образуется граница из черно-белых плиток, разделяющая черные и белые. Эти плитки можно повернуть так, чтобы замощение стало корректным. Например: n = m = 4,
a = b = 6, c = 4.
В общей ситуации заменим c - m черно-белых плиток, например, на белые и построим замощение. Затем заменим белые плитки обратно на черно-белые, начиная с правого-нижнего угла, например: n = m = 4, a = 6, b = 3, c = 7.
Решение в задаче всегда существует.
Заданный граф представляет собой связный граф с одним циклом. Сначала научимся решать задачу для дерева. Подвесим дерево за произвольную вершину и стандартной динамикой вычислим для каждого поддерева
1) количество вершин в нем;
2) сумму расстояний от корня до всех вершин поддерева.
После этого мы получим ответ на задачу для корня. Чтобы определить ответ для остальных вершин, совершим еще один обход по дереву. Рассмотрим переход от вершины u к ее потомку v. Чтобы добраться до v из вершни ее поддерева, нужно будет проделать тот же путь, что и до u, только не проходя последнее ребро. Наоборот, для всех остальных вершин путь увеличится на длину этого ребра. Таким образом, d[v] = d[u] - L(u, v) * c[v] + L(u, v) * (n - c[v]), где c[v] - количество вершин в поддереве с вершиной v.
Теперь перейдем к графу с одним циклом, к которому возможно крепятся деревья. Корнями деревьев будем считать вершины цикла. Посчитаем ответ внутри каждого дерева. Общий же ответ складывается для каждой вершины из:
1) суммы длин путей внутри ее дерева;
2) суммы для всех остальных деревьев путей от их корней до всех вершин в дереве (потому что чтобы добраться до некоторой вершины из другого дерева, нужно пройти через его корень);
3) длины пути от вершины до корня ее дерева, умноженной на общее количество вершин в других поддеревьях;
4) сумма вида <длина кратчайшего пути по циклу от корня до дерева t> * <количество вершин в дереве t>.
Наиболее трудным является вычисление слагаемого 4. Для его подсчета нужно пройти по циклу двумя указателями: на текущую вершину и на вершину в цикле, которая разделяет вершины, от которых надо идти вправо и от которых надо идти влево до текущей вершины. Двигая указатели, можно за суммарное линейное время пересчитывать частичные суммы, необходимые для получения слагаемого 4.
Задача H
Представим сначала, что у нас ровно m черно-белых плиток. Тогда можно поступить следующим образом. Будем перебирать клетки по порядку сверху-вниз слева-направо. Сначала положим a черны плиток, потом - c = m черно-белых, затем - b белых. В итоге образуется граница из черно-белых плиток, разделяющая черные и белые. Эти плитки можно повернуть так, чтобы замощение стало корректным. Например: n = m = 4,
a = b = 6, c = 4.
######## ######## #####/\# ####/..\ \##/.... .\/..... ........ ........
В общей ситуации заменим c - m черно-белых плиток, например, на белые и построим замощение. Затем заменим белые плитки обратно на черно-белые, начиная с правого-нижнего угла, например: n = m = 4, a = 6, b = 3, c = 7.
######## ######## #####/\# ####/..\ \##/.... .\/..... .../\../ ../##\/#
Решение в задаче всегда существует.











nice structure for problem h