361A - Левко и таблица

Матрица, у которой все диагональные элементы равны k, а другие 0 удовлетворяет условие. Например для n = 4, k = 7 она будет такой:

7 0 0 0

0 7 0 0

0 0 7 0

0 0 0 7

361B - Левко и перестановка

Так, как gcd(1, m) = 1, то при n = k ответа не существует.

Воспользуемся фактом, что gcd(m, m - 1) = 1 и построим такую перестановку:

n - k  1  2  3  ...   n - k - 1  n - k + 1  n - k + 2  ...   n

360A - Левко и восстановление массива

Найдем для каждой позиции i такое значение b[i], что a[i] ≤ b[i]. Что бы найти эти значения, будем симулировать операции, поддерживая массив diff[i] — разница между теперешним значением i-ого элемента и его начальным значением. Если операция первого типа, то меняем нужные значения delta[i], иначе мы знаем, что a[i] + diff[i] ≤ m[i], из этого следует, что a[i] ≤ m[i] - diff[i]. Объединим все эти неравенства и мы получим массив b.

Докажем, что либо b удовлетворяет условие, либо такого массива не существует. Возможны два варианта не выполнения операции второго типа:

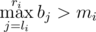1. — но это невозможно из построения массива b.

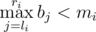2. — но мы взяли на каждой позиции максимум, то есть мы не можем получить значение 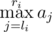больше и чтобы при этом выполнялись все другие условия.

360B - Левко и массив

Сделаем бинпоиск по ответу. Чтобы проверить можно ли достичь ответа x, сделаем дп.

dp[i] — это минимальное количество элементов, которые нужно изменить до i-ого, и при том i-ый элемент мы не меняем. Перебираем следующий элемент j, который мы не меняем. Тогда мы знаем, что элементы i и j мы не меняем, а все остальные между ними можем менять. Чтобы проверить можем ли мы так сделать, нужно всего лишь, чтобы выполнялось условие

|a_j - a_i| ≤ (j - i)·x

Это так, потому что между соседними разница может быть максимум x, а между элементами i и j ровно j - i раз разница может увеличиваться на x.

360C - Левко и строки

Посчитаем количество таких подстрок t, которые больше соответствующих подстрок s и начинаются в позиции i.

1. Если t[i] < s[i], то 0.

2. Если t[i] > s[i], то n - i.

3. Если t[i] = s[i], то найдем ближайшую позицию j,  j > i , такую, что t[j] ≠ s[j]. Если t[j] > s[j], то нужное количество подстрок будет n - j. Если t[j] < s[j], то 0.Это мы можем переформулировать так:

Если t[i] > s[i], то будет (1 + pref)·(n - i) новых подстрок, где pref означает сколько последних перед i элементов из s и t равны.

Сделаем дп. dp[i][sum] — значит, что мы просмотрели i позиций и набрали sum нужных подстрок, при этом значение t и s в i-ой позиции отличаются. Будем делать ее назад. Переберем общий префикс pref этих строк и то больше или меньше t[i].

Если t[i] < s[i], то dp[i][sum] +  = dp[i - pref - 1][sum]·(s[i] - 'a') — это посчитаем частичными сумами.

Если t[i] > s[i], то dp[i][smum] +  = dp[i - pref - 1][sum - (1 + pref)·(n - i)]·('z' - s[i]). Будем перебирать pref.

Заметим, что sum - pref·(n - i) ≥ 0, то есть pref ≤ sum / (n - i) и pref ≤ k / (n - i). Это значит, что при нахождении значения dp[i][sum] третий цикл выполнит не больше k / (n - i) итераций. Посчитаем общее количество итераций:

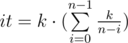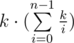 =   <  k·(n + k·log  k).

360D - Левко и множества

Так, как число p — простое, то должен существовать первообразный корень g по модулю p(Явно мы его не находим, пусть просто он есть). Тогда запишем каждое a_i = g^r_i. Заметим, что в i-ом множестве будут находиться все числа вида 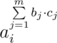, где c_j ≥ 0. Это можно записать как .

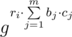Малая теорема Ферма — a^p - 1 = 1 mod p. Это также значит, что a^k mod p = a^{k mod (p - 1)} mod p. Из этого следует, что 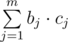может принимать все значения k·t по модулю p - 1, где t = gcd(b₁, b₂, ... , b_m, p - 1). Заметим, что t никак не зависит от r_i, поэтому мы можем сделать g = g^t. Тогда все элементы с i-ого множества будут выглядить, как g^r_i·k, где k ≥ 0. Заметим, что мы получили приктически такой же запис как и с b_i в начале, сделаем то же. Заменим r_i на q_i, где q_i = gcd(r_i, p - 1). Тогда все элементы с i-ого множества будут выглядить, как g^q_i·k, где k ≥ 0. Это значит, что если мы запишем значения g⁰, g¹, ..., g^p - 2 в строку, то в i-ом множестве будет каждый q_i-ый.

Теперь чтобы найти объединение этих множеств, нам нужно применить принцип включения-исключения. Так как все числа, которые мы маем — делители p - 1, то мы можем добавлять q_i по одному, поддержывая dp_i — коефициэнт возле i в принцыпе включения-исключения.

Нам осталось найти q_i. Рассмотрим количество элементов в i-ом множестве. С одной стороны оно равно 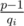. С другой стороны это количество равно минимальному такому значению d_i, что a_i^d_i = 1 mod p (d_i — цыкл). Из того что a_i^p - 1 = 1 mod p маем, что p - 1 делится на d_i. Найдем d_i среди делителей p - 1. Теперь .

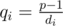360E - Левко и игра

Алгоритм:

Сначала будем решать задачу, может ли первый победить.

Сделаем все дороги, которые можно менять, равными r[i] и запустим две Дейкстры из вершын s₁ и s₂. Пусть массив d1[i] — расстояное от s₁ до i, d2[i] — расстояние от s₂ до i. Рассмотрим дорогу из a в b, которую можно менять. Если d1[a] < d2[a], то поставим длину этой дороги равной l[i] и опять запустим две Дейкстры. Так делаем пока мы можем изменить значение хотя бы одной дороги.

Если в конце у нас получилось d1[f] < d2[f], то первый может победить.

Дальше повторим тоже самое, только условие d1[a] < d2[a] меняем на d1[a] ≤ d2[a]. Это нам даст, может ли первый игрок достичь ничьи.

Доказательство:

Будем называть ребрами только те дороги, которые Левко может менять. Причем, если мы запускаем Дейкстру из какой-то вершины, то мы учитываем все дороги.

1. Докажем, что если существует расклад значений ребер, при котором первый игрок выигрывает, то существует такой, при котором он выигрывает и все ребра равны либо l[i], либо r[i]. Возьмем кратчайшие пути первого и второго игрока из данного расклада.
   Тогда если по ребру из a в b проходит только первый, то мы можем установить его значение l[i]. Доказательство: для этого ребра должно выполняться d1[a] < d2[a], потому что первому выгодно по нему проходить и он выигрывает. Это условие выполняться и после изменения значения ребра. Тогда второй либо идет по нему и проигрывает потому, что d1[f] ≤ d1[a] + d(a, b) + d(b, f) < d2[a] + d(a, b) + d(b, F) = d2[f] , либо не идет и тоже проигрывает потому, что расстояние первого уменьшилось, а его нет(d(x, y) — кратчайшее расстояние между x и y).
   Если по ребру проходит только второй, то можем поставить r[i]. Доказательство: Первый по нему проходить и так не будет, а путь второго от этого меньше не станет.
   Если по ребру не проходит ни один игрок поставим его равным r[i]. Доказательство: Пути игроков никак не изменяться.
   Если по ребру проходят оба игрока, то поставим l[i]. Доказательство: Пути обоих игроков уменьшаться на (предыдущее значение — l[i]).
   После каждой из этих операций если первый выигрывал, то он и продолжает выигрывать, но в конце у нас получаться все ребра равными либо l[i], либо r[i].

2. Рассмотрим результат выполнения алгоритма: некоторые ребра будут равны l[i], а некоторые r[i]. Назовем ребра хорошими если на них теперь стоит l[i] и плохими — если r[i].
   (a) Докажем, что в конце для всех хороших ребер выполняется условие d1[a] < d2[a]. Докажем от супротивного. Пусть у нас для ребра (a1, b1) выполнялось d1[a1] < d2[a1], а после нескольких итераций перестало выполняться. Пусть оно перестало выполняться, после изменения ребра (a2, b2). Тогда мы маем такие неравенства d1[a1] >  = d2[a1], d1[a2] < d2[a2]. Так как мы изменили только одно ребро и расстояние второго игрока до а1 уменьшилось, то на кратчайшем от него до а1 он идет по ребру (a2, b2).
   d2[a1] = d2[a2] + d(a2, b2) + d(b2, a1) > d1[a2] + d(a2, b2) + d(b2, a1) ≥ d1[a1]. Получили противоречие.
   (b) Докажем, что в конце для всех плохих ребер выполняется условие d1[a] ≥ d2[a]. Если бы оно не выполнялось, то мы продолжили бы наш процесс.
   (c) Докажем, что если для какого-то ребра стало выполняться условие d1[a] < d2[a], но на этом шаге мы его не изменили(изменили другое), то это условие не может перестать выполняться. Оно доказывается аналогично (a).
   (d) Докажем, что если у нас какое-то подмножество хороших ребер равны l[i] и для ребра (a, b) выполняется условие, то оно не может перестать выполняться после того, как мы поставим все хорошие ребра поставить равными l[i]. Для этого просто симулируем весь процесс, применяя (c).

3. Докажем, что при любом раскладе ребер(даже не обязательно только l[i] или r[i]) мы не можем получить ситуации, в которой для плохого ребра (a, b) выполняется условие d1[a] < d2[a].
   Докажем от супротивного. Пусть у нас существует такое ребро. Рассмотрит путь первого до его начала. Если на этом пути есть плохие ребра (a1, b1), то для них тоже должно выполняться условие d1[a1] < d2[a1] (Если не выполняется , то d2[a] ≤ d2[a1] + d(a1, b1) + d(b1, a) ≤ d1[a1] + d(a1, b1) + d(b1, a) = d1[a]. Противоречие.) . Возьмем первое из них. Тогда путь первого до его начала может содержать только хорошие ребра. Рассмотрим задачу, аналогичную нашей, но с финишем в вершине a1 вместо f. Плохие и хорошие ребра будут такими же, потому что они не зависят от финиша. У нас должен победить первый игрок. Изменим все ребра на l[i] и r[i] так, как мы это делали в первом пункте. Заметим, что все плохие ребра будут равными r[i], потому что первый в кратчайшем пути по них не проходит. То есть у нас получилось, что у нас только подмножество хороших ребер равны l[i] и для ребра (a1, b1) выполняется условие d1[a1] < d2[a1]. С (d) получается, что условие для этого ребра должно выполняться и после того, как мы все хорошие ребра поставим равными l[i]. А это противоречит тому, что это ребро плохое.

4. Это значит, что при любом раскладе первому не выгодно идти через плохие ребра. Поэтому мы можем всем им поставить r[i]. Теперь l[i] мы можем поставить только подмножеству хороших ребер. Пусть для него у нас выполняется d1[F] < d2[F]. Но за свойством (d) у нас это будет выполняться и если мы все хорошие ребра поставим равными l[i].

5. Заметим, что у нас доказательство практически не измениться, если Левко хочет завершить игру ничьей.