Welcome to The Editorial!

Keep the upvotes piling up! muhehe
IZ.COMPLETE.
A. Rasheda And The Zeriba
(difficulty: medium)
The first question is: When is it possible to construct a (convex) polygon from sticks of given lengths Li?
This question is answered by what's sometimes known as Polygon inequality theorem, which states that the sufficient and necessary condition is for every Li to be strictly less than the sum of all other Li. You can imagine that it works because for the endpoints of every side, the shortest path between them (equal to the length of that side) must be smaller than any other path, including the other one along the perimeter of the polygon; constructing such a polygon, even a convex one, is pretty easy, just imagine it as having sticks linked to each other that you can freely rotate. (There's a rigorous proof, but it's unnecessarily complicated.) In other words, if we denote 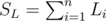 , we can't construct a polygon if there's an Li satisfying
, we can't construct a polygon if there's an Li satisfying
Suppose there's a solution. What now? Obviously, if there's a circle with radius R, we could extend some vertices (and sides) to the perimeter of the circle, and the solution still exists and is convex (any polygon inscribed in a circle is). In that case, we get something like this:

Notice the angles ai corresponding to the sides li, where li ≥ Li. For a convex polygon and its circumcircle, the center A of the circle lies in the polygon, so all the angles must sum up to 2π. If their sum is any larger, the polygon can't be inscribed in that small of a circle.
From simple trigonometry of isosceles triangles, we get 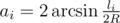 and ai ≤ π; in the range [0, π / 2], arcsine is increasing, so the condition for R to be a possible solution can be formulated as (with
and ai ≤ π; in the range [0, π / 2], arcsine is increasing, so the condition for R to be a possible solution can be formulated as (with 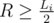 )
)
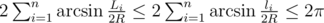
There is no nice way to simplify this and find a solution, but that's what we have computers for! If we fix R, it's easy to check the validity of this condition; therefore, we can binary-search the minimum possible R.
It's even possible to inscribe a desired polygon in the circle satisfying the equality of this condition. Just take the circle and put the sides on its perimeter in arbitrary order; the equality guarantees the last side to meet the first one correctly. The order doesn't even matter!
Since it's sufficient to consider R ≤ SL, this approach has time complexity (per test case) 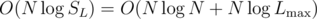 .
.
B. Egyptian Roads Construction
(diff: medium)
In most problems involving maximum/minimum edges, it's best to use a union-find data structure. That's because if we sort the edges by increasing weight and add them into the graph formed by just the N vertices, two cases can happen for an edge of cost c:
it would connect 2 vertices that have already been connected — in that case, no path will ever need to go through that edge and we can just ignore it
it'll connect two different connected components (of x and y vertices); then, all paths between pairs of vertices from those 2 components will cost c, because without that edge, there was no possible path, and adding more expensive ones doesn't decrease the cost, what means that the resulting sum for every vertex of the x will increase by cy and for those of y, the sums increase by cx
So, when adding any edge, we need to remember the connected components found so far (just as lists of vertices), the current component that each vertex belongs to; merging 2 components is done as moving the vertices of one list to another and updating the component they belong to. In order to do this quickly, we'll always merge the smaller component into the larger one.
Along with this algorithm, we also need to calculate the answers. We can't just update them for all vertices of both components in every step, though. We can do it for the smaller component — it doesn't worsen the time complexity. But, the larger one can get too large. To get around it, we'll just remember the information as "for component i, the first j vertices get answers increased by k", where j is set to be the size of this component (before the merge). It's even guaranteed that j are increasing!
These updates can be processed when the component is being merged into another as the smaller one — just process the vertices of it from last to first, remember the sum of all updates that cover the current vertex, and always check if the last unprocessed update doesn't cover it already.
With the "small to large" merging technique, every vertex is merged into another component at most  times, because after k merges, it's in a component of size at least 2k, so the sum of sizes of "smaller components" in all steps is
times, because after k merges, it's in a component of size at least 2k, so the sum of sizes of "smaller components" in all steps is  . That's also the time complexity of the union-find, because just a constant number of operations is done for every such vertex. Together with the sorting of edges, we get a complexity of
. That's also the time complexity of the union-find, because just a constant number of operations is done for every such vertex. Together with the sorting of edges, we get a complexity of 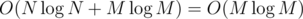 .
.
C. Tomb Raiders
(diff: medium-hard)
Let's think about a slower solution using dynamic programming. Let's say that dp[t][x][y] is the amount of treasure gained by a thief standing at (x, y) at time t. If there's A[i][j] treasure at (i, j), then we know dp[1][x][y] = A[x][y]; we're also given a way to compute other values:
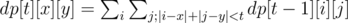
This is a straightforward way to find the result, but it's too slow. To speed it up, we'll introduce a transformation
How does this help? Notice that we can replace the condition |i - x| + |j - y| < t equivalently by 4 conditions, which must hold simultaneously:
This means that with our transformation, the cells satisfying |i - x| + |j - y| < t (some sort of diamond in the grid) becomes a rectangle, and its sum can be calculated easily using 2D prefix sums.
One way to implement the DP with this transformation is: we remember the answer for (t, x, y) in dp[t][x + y][x - y + M] (to avoid negative indexing); after calculating all the values for given t, we construct a 2D array of prefix sums S, where 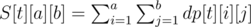 . The formula for computing dp[t][x][y] then becomes
. The formula for computing dp[t][x][y] then becomes
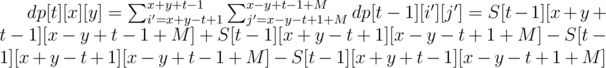
The answer is dp[T][x0 + y0][x0 - y0 + M] (T is the initial time from the input). Every element of the 3D arrays S and dp (with sizes up to T × (N + M) × (N + M)) can be calculated in O(1) time, so the time is O(T(N + M)2).
D. Bakkar And The Algorithm Quiz
(diff: medium-hard)
Let's count the number of rows that contain some marked cells (with an STL set, for example), and denote it A; the same with columns, and denote that as B. Now, w.l.o.g., let's assume A ≥ B.
It's now clear that we must use exactly A rooks — it's at least one per row, and if we put the first B rooks to different columns, then all B columns will also be covered.
The answer to the 2nd part of the problem lies in there, too. Since we use A rooks, it's exactly one rook per row; the only other condition is for all B significant columns to have rooks in them.
Once again, we'll use dynamic programming. Let's denote the number of ways to put i rooks into i rows, so that j columns still don't have rooks in them, as P[i][j]. The next rook (we put them to the rows in some fixed order) must go either to one of the j uncovered columns, giving us j possibilities to get to the state (i - 1, j - 1), or to one of the M - j covered columns, giving M - j possibilities to get to the state (i - 1, j). We can then compute P[i][j] as (M - j)P[i + 1][j] + (j + 1)P[i + 1][j + 1] (if j = B, the 2nd term is 0, so it's just (M - j)P[i + 1][j]).
The starting condition is P[A][B] = 1 (no rooks yet added), and the result can be found in P[0][0]. The modulo isn't a problem either, as we can just modulate every P[i][j] after computing it. This approach has the complexity of 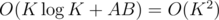 .
.
E. Ghanophobia
(diff: easy)
The result of one match is given: Egypt:Ghana 1:6. In every test case, we're given the result of the other match. This problem was pretty much just about straightforward implementation of the rules described:
if the total number of goals scored in both matches together is different for both teams, the team that scored more wins
otherwise, the team that scored more goals on enemy ground wins (if they both scored the same, it's a tie)
Time complexity: O(1).
F. Bakkar In The Army
(diff: easy-medium)
Three identities are required for this solution: 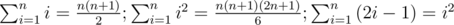 .
.
The sum of numbers in row number j is 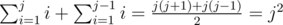 .
.
First, we need to find the smallest a such that doing all the reps in the first a rows is sufficient. That means solving the inequality 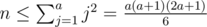 . While a constant-time solution is possible (it's a 3rd degree polynomial), it's simpler to binary-search the answer.
. While a constant-time solution is possible (it's a 3rd degree polynomial), it's simpler to binary-search the answer.
Now, let's say we know a. Then, it's necessary to do all reps in the first a - 1 rows; after that, 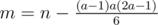 reps are left. Now, we need to find the necessary number of reps to do in the a-th row (let's denote it as b). We have 2 cases here:
reps are left. Now, we need to find the necessary number of reps to do in the a-th row (let's denote it as b). We have 2 cases here:
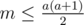 , so it's sufficient to consider the first a reps only; then, we're looking for the smallest b to satisfy
, so it's sufficient to consider the first a reps only; then, we're looking for the smallest b to satisfy 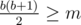
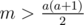 , so we need to do the first a reps (with sum
, so we need to do the first a reps (with sum 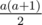 ) and then b - a more reps, with sum
) and then b - a more reps, with sum 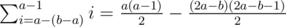 , so we're again looking for the smallest b to satisfy
, so we're again looking for the smallest b to satisfy
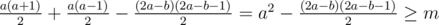
Both cases can be solved by binary search again. Now, we know a and b; all that's left is counting the reps. Since there are 2i - 1 reps in row i, the sum of reps in the first a - 1 rows is 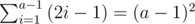 , and there are b more reps in the a-th row, so the answer is (a - 1)2 + b.
, and there are b more reps in the a-th row, so the answer is (a - 1)2 + b.
Binary searching takes  time, so this is the complexity of the whole algorithm.
time, so this is the complexity of the whole algorithm.
G. Jenga In The Military Unit
(diff: easy-medium)
The statement describes a combinatorial game with rather unusual rules. A bruteforce solution would use dynamic programming, which would determine for every state whether the player whose turn it is has a winning strategy (W state) or doesn't have any (L state).
The states are defined like this: a state (i, j, k) means there are i floors with 3 blocks each (excluding the topmost one of those), j floors below the topmost full floor with exactly 1 side block removed, and k blocks on the topmost incomplete floor (even when k = 0). Notice that instead of a state (i, j, k + 3), we could as well write (i + 1, j, k), because a new topmost full floor has been constructed.
We have at most 3 types of moves available from state (i, j, k): - if i > 0, take the center block of one full floor, moving to the state (i - 1, j, k + 1) for k < 2 or (i, j, k - 2) for k = 2 - similarly take the side block of one full floor, now moving to the state (i - 1, j + 1, k + 1) for k < 2 or (i, j + 1, k - 2) for k = 2 - if j > 0, take one side block from those j, moving to the state (i, j - 1, k + 1) for k < 2 or (i + 1, j - 1, k - 2) for k = 2
The states form a directed graph; this graph is acyclic, because in every step, the sum S = 6i + 3j + 2k decreases, so the game is finite, and we can use dynamic programming to calculate for the states whether they're winning or losing. The condition for a state to be W is: there's a move from this state to a state which is L (that also means all states from which there's no move are losing).
Using this dynamic, we can find the values in some few small states (code here, with the values of states plotted in (i, j) coordinates; read the code to get what the output means). Notice that there's a 3x3 pattern (for i > 0) that always repeats itself. Since the value of a state depends only on values of states close to it, even as we tried to calculate many more states, we'd get the same results as for i or j smaller by 3. So, we can predict that the states we're actually interested in, that's with j = k = 0, are L for 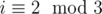 , and W otherwise.
, and W otherwise.
That means we only need to check if N (e.g. i + 1) is divisible by 3, because only then can the 2nd player win. Time: O(1) per test case.
I got AC on this problem really soon with a stroke of luck. I though: so, we have a "value of the game" N. If N = 0, we lose. We're taking the center block, forbidding 2 side blocks to be moved ever again, or the side block, forbidding the center one to be moved. So we decrease the value of the game by 1 or 2 in every step, and the W/P positions for N from 0 are P,W,W,P,W,W,...; it's clear that this idea is wrong and ridiculous, but it happens to give the correct answers. As Baklazan says: luck is a skill, too :D
H. The Job Interview
(diff: hard)
My solution for this problem uses backtracking, guesses on test data and optimizations. Eww...
A simple bruteforce would try some combinations of choosing specified sums, get the numbers on the 2 dice (let's call them A[1..6] and B[1..6] and say that we're given sums V[1..N], all in increasing order), generate their sums and try comapring them to the given ones, until it found an answer. There are around 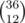 possibilities, which we want to reduce as much as possible.
possibilities, which we want to reduce as much as possible.
The first thing to note is that A[1] and B[1] can be arbitrary, as long as their sum is equal to V[1] (the smallest sum). If we define a[i] = A[i] - A[1], b[i] = B[i] - B[1], then by adding a[i]s and b[i]s, we get the same sums as from A[i]s and B[i]s, just decreased by V[1] (let's say these are v[1..N]). Let's set A[1] = 1;B[1] = V[1] - 1, then, and work just with a, b and v.
Next, notice that the order of the die doesn't matter. The sum v[2] must be equal to a[2] or b[2] (any other sum must be greater than one of those numbers), so let's choose v[2] = a[2]. We're left with 9 states now.
Let's try to construct a sequence of sums: if (i, j) = a[i] + b[j], then we're looking for (2, 2), (3, 2), (3, 3), (3, 4), (4, 4), (5, 4), (5, 5), (5, 6); we also know that the sum of 2 largest numbers, a[6] + b[6], is the largest sum, v[N], so we can reconstruct a[3..6] and b[2..6] from these numbers and a[2]. That's just 8 sums required, and these can't be v[1], v[2] or v[36] (those are too small or too large), so we have 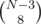 possibilities; that's around 107 for N = 36.
possibilities; that's around 107 for N = 36.
That's still not enough, no matter how hard we optimize. Even if one test case runs in under 1s, it's too slow for T = 100. But it's likely that most of those will have N = 36, because that's when the backtrack is slowest. Let's use that to our advantage.
There are at most 36 different sums; if N < 36, some sums are duplicate, and info about that is not given in the input, but if N = 36, every sum appears in the input exactly once. If we sum up all those 36 numbers, every number A[i] and B[i] is added to the sum exactly 6 times, so that sum divided by 6 gives the sum of all A[i] and B[i]! We have one more piece of information that allows us to cut down 1 sum to look for. And why not make it the sum (5, 5) — we use that to count B[5] from A[5], but if we know the sum of all A[1..5], B[1..4] and V[N - 1] = A[6] + B[6], we can get B[5] (or b[5]) directly from the sum of all V (or v). With this, we only have 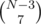 possibilities to check, which is much better.
possibilities to check, which is much better.
Still, the program needs many tiny optimizations that make us not search too far off in the sums, trash solutions which give sums other than those in the input as soon as they're found, etc. One noteworthy optimization is that v[3] will be either a[3] or b[2] — all other sums are too large or assigned to v[1] and v[2]. In the end, I take around 10s with time complexity O(exp(N)).
I got asked about how I'd solve this problem some time ago by one of the organizers of this ECPC contest. I answered with some of the things above and clever bruteforce (of course, I meant the solution if there was 1 test case and 1-2s time limit). And it seems that with 0.15 s per test case, this was really the hardest problem here.
I. Bakkar In Zanzibar
(diff: easy-medium)
This problem had suprisingly few accepted solutions. The key to it is in realizing that there are reasonably many prices P ≤ 1 that can be written as
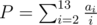
e.g. can be paid exactly; ai represents the number of times we used an  coin (we can replace an
coin (we can replace an  coin by a copies of a
coin by a copies of a  coin).
coin).
One way to generate all P is by doing a BFS on a directed graph, whose vertices are all prices 0 ≤ P ≤ 1 and an edge corresponds to adding a coin of value  (b ≤ 13). We'll also store all visited vertices in an STL set (S), in order to be able to check if it's been visited before. It's not hard to see that if we start with P = 0, we'll find all possible prices.
(b ≤ 13). We'll also store all visited vertices in an STL set (S), in order to be able to check if it's been visited before. It's not hard to see that if we start with P = 0, we'll find all possible prices.
Now, we need to answer queries. If we represent prices as fractions and sort them by value, it's enough to consider the smallest P that's not smaller than 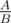 , and largest P that's not larger than
, and largest P that's not larger than 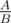 . Those can be found using the
. Those can be found using the set::lower_bound function; all that's left is to subtract those fractions from 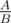 and choose the smaller absolute difference.
and choose the smaller absolute difference.
Since |S| = O(1), the pre-computation and answering one query takes O(1) time. In terms of maximum b (bm), our algorithm is clearly at least exponential — more precisely, 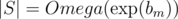 (meaning Ω(αbm) with α being some unknown constant); from every vertex of S, there are around bm outgoing edges, and operations on S (as an STL set) run in
(meaning Ω(αbm) with α being some unknown constant); from every vertex of S, there are around bm outgoing edges, and operations on S (as an STL set) run in 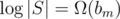 time, so the complexity is
time, so the complexity is 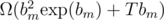 .
.
Notice the Ω- instead of O-notation — in this case, we don't show how good the algorithm is, but how bad it is — but it still runs in less than 0.2s in my implementation. Sometimes it's just important to not get scared of a problem.
J. Anniversary Gift
(diff: hard)
The key to this problem is the sentence: "For each test case, there is no more than 10 different values for each of the price, height, width, thickness and weight." How many people didn't notice this? I didn't, at least :D
The first thing that comes to mind is compression of coordinates (if we imagine the phones as points in 2D). Let's just sort and re-number the values of every parameter by their order, starting from 1. If a query asks for the range (a, b] of some parameter, we can just replace b by the largest value of this parameter ( ≤ b) that some phone had before the compression, and then replace it by the value that phone had after the compression; similarly with a. Such operations don't change the set of phones corresponding to that query. We're given [a, b], but that's the same as (a - 1, b]; we also convert doubles to integers by multiplying by 1000.
Now, we can use 5D prefix sums. Define a 5D array S containing the answers to queries with first 5 numbers equal to 0 (no lower bounds on coordinates). The value of S[i][j][k][l][m] can be found by DP, using the principle of inclusion and exclusion of sets: first, say that it's equal to the number of points exactly at those coordinates; then, add the numbers of points in all sub-5D-cubes that are smaller than the cube given by corners (0, 0, 0, 0, 0) and (i, j, k, l, m) in only one coordinate and only by 1 (like S[i][j - 1][k][l][m]), then subtract those smaller by 1 in two coordinates (like S[i][j][k - 1][l][m - 1]), etc. up to adding S[i - 1][j - 1][k - 1][l - 1][m - 1]. If you write the number of times every point in the whole (i, j, k, l, m) hypercube is added-subtracted, you'll find out it's exactly once (I won't post the proof here as it's a fairly well-known principle); to imagine it better, you can try a 2D or 3D case instead. A simple implementation uses iterating over bitmasks and transforming them into those 5D-hypercubes.
We'd now know how to answer queries without lower bounds on coordinates. Still, that's not enough. We'll use the inclusion-exclusion principle once again: we want to know the number of points in the 5D-cube with vertices (i1 + 1, j1 + 1, k1 + 1, l1 + 1, m1 + 1) and (i2, j2, k2, l2, m2). That cube can be constructed by adding/subtracting cubes with one vertex at origin (0, 0, 0, 0, 0) and each coordinate chosen to be either 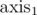 or
or 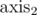 ; if the number of coordinates of the first type is even, we add, and if it's odd, we subtract. Once again, bitmasks help, and the proof is just a more general one than the one for constructing S.
; if the number of coordinates of the first type is even, we add, and if it's odd, we subtract. Once again, bitmasks help, and the proof is just a more general one than the one for constructing S.
There are 25 = 32 bitmasks to use, and every coordinate can have at most 11 values (including 0 for "-inf", for which we know the answer to be 0), so constructing S takes O(115 + 32·105·5) operations per test case, and answering a query takes just O(32·5) operations. Sorting and coordinate compression takes  , so the total complexity is
, so the total complexity is 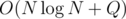 per test case, although it's plus a large constant (watch out, it's really large — you might TLE just because your implementation has a large constant of its own).
per test case, although it's plus a large constant (watch out, it's really large — you might TLE just because your implementation has a large constant of its own).
K. Cubes Shuffling
(diff: easy)
How many times is the cube at the position i (1-based) added to the total sum of subranges? The answer is obviously equal to the number of subranges it's in. The first cube of those subranges can be any one from 1 to i (so there are i ways to choose it), and the last cube of it can be any one from i to N (N - i + 1 ways to choose it); in total, it's i(N - i + 1) = - i2 + i(N + 1) ways.
We can see that this is maximum for 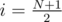 and decreases with increasing \left|i-\frac{N}{2}\right|, because the i-s are just points on the downwards open parabola described by f(x) = - x2 + x(N + 1). As a consequence of the rearrangement inequality, we want to put the largest cubes to the smallest values of f to get the smallest sum; that means we want N and N - 1 to be at positions 1 and N; cubes N - 2 and N - 3 at positions 2 and N - 1, etc. up to 1 (for N odd) or 1 and 2 (for N even) being at the position(s) closest to
and decreases with increasing \left|i-\frac{N}{2}\right|, because the i-s are just points on the downwards open parabola described by f(x) = - x2 + x(N + 1). As a consequence of the rearrangement inequality, we want to put the largest cubes to the smallest values of f to get the smallest sum; that means we want N and N - 1 to be at positions 1 and N; cubes N - 2 and N - 3 at positions 2 and N - 1, etc. up to 1 (for N odd) or 1 and 2 (for N even) being at the position(s) closest to 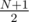 .
.
We also want the order to be lexicographically minimum. That means we always put the smaller cube (if we have a pair) to the smaller position (N - 1 to position i, N to pos. N, etc.).
Time complexity is O(N). It's just straightforward implementation of the described idea.
L. Mahdi And The Teddy Bear
(diff: easy-medium)
The solution described here works in O(N) memory.
If we had N = 1, the problem would be just about checking whether a string T is a substring of string S. That can be done with a single linear pass of S — remember the largest a such that the prefix of T of length a has already been seen in S as a subsequence; if we encounter some character of S equal to the next letter of T (right after that prefix), we can increase a by 1 (we've seen the prefix of length a + 1 as a subsequence of S). This clearly works, because there's nothing we can gain by deciding to try some other letter of S to be that next letter of T — we won't get any better chances of the answer being YES. The answer is YES iff, at some point, 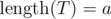 .
.
That can be viewed as T being in the state a, and possibly moving to state a + 1 if the "next" letter of T (by the random letter generator described in the problem statement) is equal to that of S. Let's extend this idea to N strings: string T[i] is in state ai. We can't afford to check for every letter of S and all T[i], whether the next letter of T[i] is equal to the one of S, but since there are just 26 possible letters, we can group the states of T-s that have the same next letter, as pairs (i, ai) in vectors.
We'll generate the letters of S; if we've generated c, we'll take all strings with c as the next letter, increase their a-s by 1, for each of those strings generate its new next letter (if we're at the end, the answer for that string is YES and we'll just delete it), and move it to the vector of states corresponding to that letter. If, at the end of the pass, the state of some string hasn't been 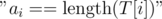 , the answer for it must be NO.
, the answer for it must be NO.
Since we only increase states' a-s as many times as the sum of all letters in all N strings, and generating new letters takes constant time, the complexity per test case is 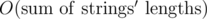 .
.
Fun fact: this problem, although with explicitly given strings, appeared in the Slovak (and Czech) OI, round 2, so I knew the solution.











I don't understand the analysis of problem G. We can increase number of un-takeable blocks by 3 or 4 using condition that it is only allowed to remove a block from a level that is fully covered from the top(how do we use it by the way?). Why is X=N a losing position?
Sorry, levels and blocks got mixed up. I though this worked as a rough idea, at first. I have a proper strategy and will post it soon.
For question A, when I compare the angle <= 2 * pi, I get AC whereas angle < 2 * pi + eps gets WA where eps = 10 - 9 and pi = acos( - 1.0). Can you please confirm if it is some issue with my implementation or a bug on the judge side? Which value to keep for eps for comparison? What are general good methods to avoid precision issues?
All submissions are getting "Denial of judgement" on problem B and J. Is there anyway to get this fixed?
Xellos, could you reupload the image you used to explain the solution for problem A?
@Xellos
Unfortunately no. I haven't kept the image on my computer for years. Imageshack cancelled free sharing so image is gone, unless you know how I can still get it from Imageshack.
Web archive saved it