Thanks for participating in the round! We hope you enjoyed it.
In addition to the usual text-editorial below, namanbansal013 will explain Div. 2 solutions on his stream, and ak2006 has made video explanations for Div. 2 B, C, D, and E.
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...










So fast editorial!
Thanks for the fast editorial ;)
for D
a bxx ba => abxxba , which is a palindrome and it requires concatenating 3 strings
isn't this a counter example for the proof
Why should it be a counterexample? Taking pairs still works, as you can use only the first and last element and get the palindrome
aba.Also, note that
aby itself is already a palindrome ;)a ba is enough
only a is enough as a single character is a palindrome
For problem D
s1 = "abcd"
s2 = "edc"
s3 = "ba"
It requires concatenation of all 3 strings to be a palindrome => "abcdedcba".
Isn't it a counter example? if not plz explain.
You mean Div.2 D?
The length of s is at most 3, so "abcd" is illegal.
In D1 you didn't need to have a constraint on sum of $$$n$$$, because $$$dp_k[n][m] = dp_1[n][m] \cdot k$$$ and everything can be precalculated in $$$O(maxn^2)$$$
True, but we wanted the easy version to be strictly easier than the hard version.
I didn't read the constraint on n in the harder version (facepalm) and had the solution formula written on paper for a solid 20 minutes in contest thinking that an O(n) per testcase solution TLEs...
So did I!!
I didn't notice it at first too. Just after I relalized that "I probably can't precalculate everything and it seems hard to make it faster than linear" I have re-read it.
By the way
is technically incorrect, the difference is the constraints on $$$n$$$, $$$m$$$ and $$$t$$$ and sum of $$$n$$$
Could anybody prove why I was able to cheese D:143658044? I simply handled trivial cases separately and then ran a nested loop with early exits and it somehow passed
Uphacked. To be fair, it's hard to prepare a test case that breaks your solution without seeing your solution beforehand, so I can't really fault problemsetters for missing this test case.
Hey, I have a similar issue in problem C, I think my solution should give TLE to a test case where the array a is n consecutive numbers between 0 and n-1.
Here's my code.
Since I'm using a set, I don't know how to traverse only the values greater than the previous MEX, so I'm traversing the entire set at each iteration.
Thank you in advance :)
Yes you're right, the solution gets hacked with an array from $$$0$$$ to $$$n - 1$$$. Instead of resetting the mex to 0 each time you have to update the mex, note that the mex always monotonically increases, so you can just start incrementing mex further. This bounds the work done by $$$\mathcal O(n)$$$.
Thank you so much, I already fixed it. But, I wonder why this test case was not included in the testing phase, my idea's pretty similar to the editorial one. Don't get me wrong please, the contest was great, but my code fails to find the MEX of the subarray in an optimal way. This test case should have been used during hacking phase.
How the time complexity of this is o(N)?
The value of the MEX is monotonically non-decreasing, so each time a new element of the array is parsed, the MMEX is incremented or kept. Since there are n elements in the array, the while loop will do at most n iterations. Total time complexity O(N*logN).
Good catch, but what about this one: 143751547? Now I remove duplicates and random shuffle for better luck, so I think it's way stronger.
This one was much harder to hack but still possible. Basically I only have one pair in the input that forms a valid palindrome. Then it just comes down to how lucky you get with the random shuffle and if you reach the valid pair early enough. I had two unsuccessful hacking attempts at first simply because of the randomness, so this submission would definitely be difficult to hack in a real contest scenario.
I have implemented div 2 c in this link but it is giving me a memory limit exceeding error. Can any one pls suggest where I have implemented it wrong.
Maybe because you are making too many vectors(which have values stored in them) inside a method which is running recursively. Without comments it hard for me to see what you are trying to do hence it is only a guess.
.
CDEF div2 are ABCD div1, aren't they?
Another solution for problem D1C(D2E): Try to take the XOR of the red cells in the picture, then what happened?
code: 143676971
Nice Solution! How did you come up with this configuration of cells in the contest?
When I drew a chess-board pattern, diagonal lines are dimly seen...
oh wow! got it. Thanks.
What kind of sorcery is this.
Nice Solution!Thanks for your great idea!
My solution for D2C is slightly different
If MEX of the entire array is mex and mex is small then we should remove as many equal mexes as possible. This way we guarantee that next mex will be even smaller
On the other hand if mex is large, then we already remove a significant number of elements
This way removing part becomes cheap because the total number of iterations when we actually remove becomes small
The complexity seems to be O(n * sqrt(n))
Thank you for this nice Mihai round ! I hope to see more Mihai rounds in the future !!
For C we can prove that any initial arrangements of row 1, yields a valid unique solution that can be constructed greedily. This is done by choosing row 2 in such a way it makes row 1 valid, and its obvious to see there is just one solution for that.
Let us assume there exists some solution. If we swap some element in row 1, $$$(1,x)$$$ you can notice it will change elements $$$(2,x+1)$$$ and $$$(2, x - 1)$$$, which will similarly change $$$(3, x - 2)$$$, $$$(3, x)$$$, $$$(3, x+2)$$$. By $$$\frac{n}{2}$$$ rows it will just swap $$$(\frac{n}{2}, 2x)$$$ or $$$(\frac{n}{2}, 2x + 1)$$$ for all $$$x$$$. This will make no difference in the last row, as it symmetrically loops after that. All other rows are taken care of in propogation.
Hi, can someone please explain this proof of the editorial construction in a bit more detail? I am unable to understand even from the above proof. Thanks in advance.
Could you explain that why "by n/2 rows it will just swap (n/2, 2x) or (n/2, 2x+1) for all x"? I have thought it carefully but I still can't understand that, thanks. :)
Nice solution! jschnei and I had a bit of trouble following your write-up, but eventually we figured it out, so hopefully this comment helps anyone else in the same boat.
The idea is that you can basically fill a $$$45^{\circ}$$$ rectangle with a checkerboard pattern and it perfectly touches all 4 sides of the $$$n \times n$$$ grid.
Example:
Notice that every cell is adjacent to an even number of
Xs, and we can change how we construct this rectangle to place exactly 1Xin the top row wherever we want. Then we can xor this pattern with any valid solution to get a valid solution with 1 cell of the top row toggled.Thank you a lot! :P
Thanks for sharing. I understood the pattern in figure but how does it prove the original construction in editorial. By toggling a cell (1, x) in row 1, do you mean that we take that cell by querying the below cell (2, x) which in turn triggers this pattern?
The greedy approach is that if (x, y) is calculated even times, you should choose (x+1, y).
Assume there is a soltion, call it S. By toggling (1, x), the greedy approach will generate the pattern above. If more than one cells in row 1 is toggled, the result is the xor of their patterns. Now for any initial arrangements of row 1, they all can be treated as S toggled some cells in row 1. So the approach will works.
Also to mention that the proof is based on the fact that there is at least one legal solution, you can prove it by the solution 2 in the editorial.
Thanks a lot AnandOza for clarifying the statement. So this means that if we have an original grid $$$orig$$$ satisfying the given XOR-sum grid, and we XORed the value of a cell with position $$$(1, c)$$$ with $$$x$$$ (for each bit set in $$$x$$$, toggle it in $$$(1, c)$$$), we need to XOR cells marked by $$$X$$$ in the other rows with $$$x$$$ for the XOR-sum grid to be the same.
So this proves that a first row with arbitrary values always belong to a grid $$$g$$$ satisfying the given XOR-sum grid, as row $$$1$$$ in $$$orig$$$ can be converted to row $$$1$$$ in $$$g$$$ using the previously mentioned operation on each cell.
However, unlike the Editorial says, I do not think this proves the greedy strategy mentioned there. The strategy mentioned in Everule's solution retrieves one of the grids satisfying the given XOR-sum grid and calculates its total XOR-sum.
However, the Editorial's greedy strategy operates on the XOR-sum grid directly. It guarantees that after processing row $$$r$$$, all the cells of row $$$r-1$$$ in the original grid will be used odd number of times. But what guarantees that after processing row $$$n$$$ the cells of this row itself will be used odd number of times as well?
To answer the previous question, I tried to write the pattern of used cells in the XOR-sum grid for multiple values of $$$n$$$, and found that they always satisfy some recurring strategy which I tried to explain here.
I have another solution to C :
Let paint the grid with white and black .
(i,j) is black if i+j mod 2 =0, else it is white
the value of A ,is the xor sum of "1" grids .
And the xor sum of B is the xor sum of "2" grids and "1" grids.
The xor sum of C is the xor sum of "3" grids and "2" grids .
Now we can know the xor sum of all white grids .
Do the same for the black one . We can get the answer .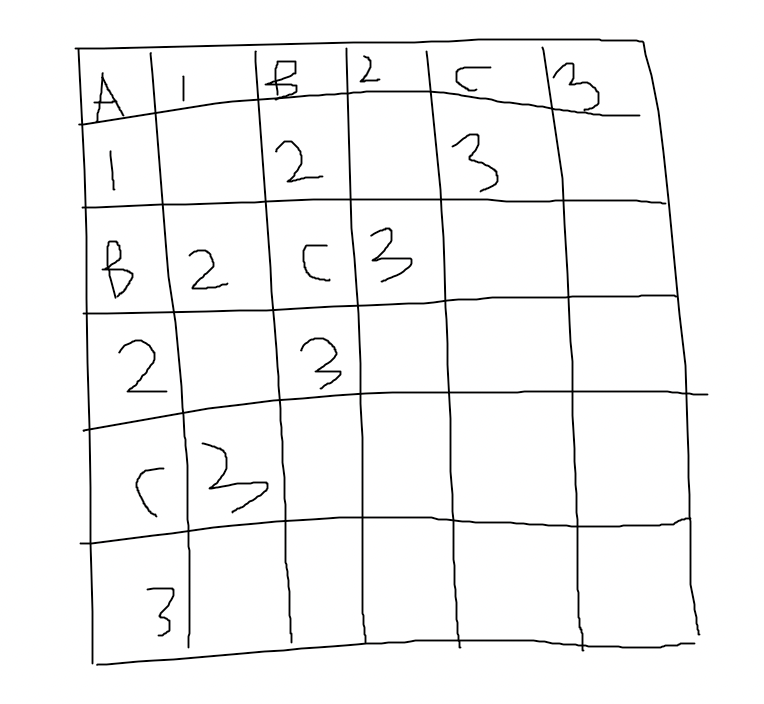
Thanks for your solution. I was thinking in a very similar direction during the contest but couldn't complete my solution, maybe since, I had never solved such a problem using a checkered board or bipartiteness in a grid.
There's a typo in the editorial of Problem D2. $$$DP[i][i] = i$$$ should be replaced by $$$DP[i][i] = k \cdot i$$$
Cc: SlavicG magnus.hegdahl
I've found an alternative solution to Div2 C — Meximum Array that is quite elegant, if I may say so myself.
Let's keep track of current MEX value, which is initially zero, and look at each array element from left to right. We can store already seen array elements in a hash table, std::set or an array of size $$$2 * 10^5$$$ and update MEX value in $$$O(n)$$$ time. Notice that MEX can only change it's value when it's equal to current array element — and also that it can only grow. If we could somehow predict the future and know that we won't ever encounter an element equal to MEX, then we could conclude that current value of MEX is global maximum for entire array, add it to answer and reset MEX-tracking machinery (set current MEX value to zero and forget all seen elements). But we can do exactly that, we can predict the future in $$$O(1)$$$ time if we spend $$$O(n)$$$ time in preparation — for that we need to store count of not-yet seen elements for each element value in a hash map or an array and later update (decrement) it when going over each element from left to right.
Final complexity depends on what data structure we use for storing seen and unseen elements. I've got TLE with std::vector of size $$$2*10^5$$$ and using std::fill to reset it because of large hidden constant, but a solution with std::unordered_map was accepted.
Here is my code: https://mirror.codeforces.com/contest/1629/submission/143691434
Hi,I have a question here. How to find out prefix mex for an array in O(n) or O(nlogn) ? I mean, for each i from 1 to n,I want to find out mex from 1 to i ,
Amortized cost is linear.
This was my idea but I don't know what's wrong in this.
Traverse from back and find the max element that you've encountered till i, store this in the "Back" array;
Now traverse from front and keep inserting v[i] onto the set s. Let mFound be the max(mFound, back[i]) Now if s.size() == mFound + 1, that means we have all the elements less than mFound add mFound + 1 into the ans array, and reset set s. Also setting last_index to i.
For the end, ex, 0 2, the ans should be 1, so we traverse from the last_index+1 to n and find the minimumn no not available.
143663484
Peculiar Movie Preferences Video Solution.
Don't forget to like and subscribe!!
https://www.youtube.com/watch?v=xBkDyMHVTJ0
If anyone's wondering, here's the genfunc sol for D2...
So, for Div. 1 D1, we can determine that the solution is
Let $$$A_n(x) = \sum\limits_{i=0}^{n} D[n][i] x^i$$$, then the recurrence above rewrites as
This rewrites explicitly as
Thus the final answer is
Unfortunately, it took me quite a while to derive everything and I could only solve it after the contest has ended :(
I think, one can also find a closed formula for $$$A_n(x)$$$ as a rational polynomial function, so it should be possible to calculate $$$D[n][m]$$$ for a fixed $$$n$$$ and all possible $$$m$$$ in something like $$$O(n \log n)$$$.
Finding the rational function actually gives you a way to compute it for all possible values in $$$O(n)$$$.
I'll assume $$$k = 1$$$, since you can just multiply by $$$k$$$ at the end. Let $$$a(x) = \frac{1 + x}{2}$$$. Now the equation,
On differentiating,
I'll call the above expression $f(x)$ for now.
Now, rewriting
Plugging this in and simplifying, you end up with
You can compute $a(x)^n$ in $$$O(n)$$$ using Binomial theorem, dividing by $$$1 - x$$$ is the same as computing partial sums of the numerator (equivalently, divide using long division) so you can compute the whole thing in $$$O(n)$$$. 143777320
Edit: I played around it with a bit and you can get a cleaner expression,
However, you can get rid of the two $x^n$, $$$x^{n + 1}$$$ terms from the numerator as they only make sure that $$$[x^m] A_n(x) = 0$$$ for $$$m > n$$$. Ultimately, you end up with the very slick,
for $0 < m \le n$. 143779641
Regarding the editorial of Problem D2:
I think the reason why the $$$x$$$ value that maximises the expression $$$min(DP[i−1][j−1]+x,DP[i−1][j]−x)$$$ is always valid (namely, $$$0 \le x \le k$$$ is satisfied) should be mentioned in the analysis of the solution.
Cc: SlavicG magnus.hegdahl
If anyone is interested, I will put a proof here. But it's not a short proof, so I might have overcomplicated it. If anyone has a simpler proof, feel free to share it. Maybe there is some obvious observation that I'm not seeing.
First I need to prove the following lemma.
Statement: $$$S_i = \frac{1}{2}(DP[i][i] - DP[i][i - 1]) = \frac{k(2^i - 1)}{2^i}$$$ , for all $$$i \geq 1$$$
Proof:
By induction on $$$i$$$.
Then the proof of what you asked for:
We want to prove that $$$0 \leq x_{i,j} = \frac{DP[i - 1][j] - DP[i - 1][j - 1]}{2} \leq k$$$, for any $$$1 \leq j < i \leq n$$$. Let's prove it by induction on $$$i$$$.
Now we want to prove it for $$$i + 1$$$:
$$$x_{i + 1, j}= \frac{DP[i][j] - DP[i][j - 1]}{2}$$$
Let's split it into 3 cases:
$$$x_{i + 1, 1} = \frac{DP[i][1] - 0}{2}$$$
Using the recurrence definition of $$$DP[i][1]$$$: $$$x_{i + 1, 1} = \frac{DP[i - 1][1]}{2}$$$
Then, using the inductive hypothesis with $$$j = 1 \Rightarrow 0 \leq \frac{DP[i - 1][1]}{2} \leq k$$$
By the previous lemma, \begin{equation} 0 \leq \frac{DP[i][i] — DP[i][i — 1]}{2} = \frac{k(2^i — 1)}{2^i} \leq k \end{equation}
$$$x_{i + 1, j}= \frac{DP[i][j] - DP[i][j - 1]}{2}$$$
Using the recurrence definition of $$$DP[i][j]$$$ and $$$DP[i][j - 1]$$$: \begin{equation} x_{i + 1, j}= \frac{DP[i — 1][j] + DP[i — 1][j — 1]}{4} — \frac{DP[i — 1][j — 1] + DP[i — 1][j — 2]}{4} \end{equation}
Reordering the terms: \begin{equation} x_{i + 1, j}= \frac{DP[i — 1][j] — DP[i — 1][j — 1]}{4} + \frac{DP[i — 1][j — 1] — DP[i — 1][j — 2]}{4} \dots(1) \end{equation} By inductive hypothesis: \begin{equation} 0 \leq \frac{DP[i — 1][j] — DP[i — 1][j — 1]}{2} \leq k \dots (2) \end{equation} \begin{equation} 0 \leq \frac{DP[i — 1][j — 1] — DP[i — 1][j — 2]}{2} \leq k \dots (3) \end{equation} Finally, adding (2) and (3) and dividing by two, we get: $$$0 \leq x_{i + 1, j} \leq k$$$
$$$\blacksquare$$$
Your proof can be made pretty short, just get rid of the lemma. You need to prove that $$$DP[i][i] - DP[i][i - 1] \le 2k$$$. You know that $$$DP[i][i] = ik$$$, so equivalently you have to prove that $$$(i - 2)k \le DP[i][i - 1]$$$.
This is true because Alice has a strategy to force a score of $$$(i - 2) k$$$. Always pick $$$k$$$, Bob needs to do $$$i - 1$$$ additions and $$$1$$$ subtraction, giving a score of $$$(i - 1) k - k = (i - 2) k$$$.
(actually its the same as all the written above)
I think its much simpler proof:
Lets prove by induction, that for $$$\forall n>0$$$ and $$$\forall i,~0\le i\le n$$$ that $$$0\le DP[n][i+1]-DP[n][i]\le 2k$$$
base: $$$n=1:0\le DP[1][1]-DP[1][0]=k-0=k\le 2k$$$
induction step: statement holds for $$$n$$$, lets prove it for $$$n+1$$$
$$$~~~~~~~~~~~~~~~~~~~~DP[n][0]~~~~~~~~~~DP[n][1]~~~~~~~~~~DP[n][2]~~~~~~~~~~DP[n][3]~~~~~~~~~~\ldots~~~~~~~~~~DP[n][n-1]~~~~~~~~~~DP[n][n]$$$
$$$DP[n+1][0]~~~~~DP[n+1][1]~~~~~DP[n+1][2]~~~~~DP[n+1][3]~~~~~\ldots~~~~~\ldots~~~~~\ldots~~~~~\ldots~~~~~DP[n+1][n]~~~~~DP[n+1][n+1]$$$
for $$$1\le i\le n-1$$$ its obvious that $$$0\le DP[n+1][i+1]-DP[n+1][i]\le 2k$$$ because distance between adjacent numbers on the second line is equal to the distance between middles of the adjacent numbers of the first line, because $$$DP[n][m]=(DP[n-1][m-1]+DP[n-1][m])/2$$$)
so we must only prove the statement for $$$i=0,n$$$
lets prove for $$$i=0$$$
we must prove $$$0\le DP[n+1][1]-DP[n+1][0]\le 2k$$$
$$$DP[n+1][1]-DP[n+1][0]=DP[n+1][1]-0=(DP[n][1]+DP[n][0])/2=DP[n][1]/2$$$
we know that $$$0\le DP[n][1]-DP[n][0]=DP[n][1]\le 2k$$$
$$$0\le DP[n][1]/2\le k$$$
so $$$0\le DP[n+1][1]-DP[n+1][0]=DP[n][1]/2\le k\le 2k$$$
now lets prove for $$$i=n$$$
we must prove $$$0\le DP[n+1][n+1]-DP[n+1][n]\le 2k$$$
$$$DP[n+1][n+1]-DP[n+1][n]=k(n+1)-(DP[n][n]+DP[n][n-1])/2=k(n+1)-(kn+DP[n][n-1])/2$$$
we know that $$$0\le DP[n][n]-DP[n][n-1]=kn-DP[n][n-1]\le 2k$$$
$$$kn\ge DP[n][n-1]\ge kn-2k$$$
$$$DP[n+1][n+1]-DP[n+1][n]=k(n+1)-(kn+DP[n][n-1])/2\le k(n+1)-(kn+kn-2k)/2=k(n+1)-kn+k=2k$$$
$$$DP[n+1][n+1]-DP[n+1][n]=k(n+1)-(kn+DP[n][n-1])/2\ge k(n+1)-(kn+kn)/2=k(n+1)-kn=k\ge 0$$$
so $$$0\le DP[n+1][n+1]-DP[n+1][n]\le 2k$$$
pronblem B was hell for me because i am not really good at math problems otherwise everything was perfect thanks for this round
Did someone else not notice D2 having the "sum of N is bounded" restriction and sat on the solution for half of the contest? :|
I didn't solve E during contest, but I solved it after contest! Here's the solution:
Observation 1: We know that our final answer will just be the bitwise XOR of some elements of our grid. This is kind of hard to prove (I think), but it's intuitive enough.
Observation 2: We're choosing some subset of elements in our matrix and bitwise XORing all of those elements which we chose.
Observation 3: We can imagine this as a binary matrix, where 1 means that we chose that element and 0 means that we do not chose that element. We want to construct the matrix in such a way that each element has an odd number of neighbors which are 1. That way, we include everything in our bitwise XOR.
Observation 4: If we fix some row of our boolean matrix, the rest of the matrix is fixed.
Observation 5: If we fix the first row to contain only ones, we're done.
So the idea is to fill the first row with ones and then fill out the rest, which is fixed.
143706309
I appreciate you wrote all those observations. Very easy to follow. Thanks.
For Problem Div2 D, tags are showing twice.
Where does my solution for C go wrong? I didn't do anything with suffixes so that may have been an issue but I fail to see how $$$\text{MEX}(l,N)$$$ and $$$\text{MEX}(r,N)$$$ could be used to calculate $$$\text{MEX}(l,r)$$$ (following the notation of the editorial).
If we calculate MEX of all suffixes then we can get MEX(i,n) for any i, which is what editorial is asking to do.
Think in this way — Reverse the array and then calculate MEX till each index. This is same as MEX of a suffix in original array.
Edit — Take this example : -
a,b,c,d,e
If we want to know MEX of c to e, we can easily do it if we have calculated MEX of e to c, since both are same.
Please forgive me if i'm wrong, but we need not only MEX(i,N) but also MEX(i,j) because in editorial (at paragraph 3) we calculate MEX(p,j) where p and i are some numbers from 1 to n. But in editorial there is nothing about it (and in your answer too) only about to calculate MEX(i,N). I have the same question — how we can calculate MEX(i,j) or why we have not to do it. Thanks in advance.
This is the comment I was looking for. The way I did it was based on sets. I took a set and initially kept from 0 to n. From 0 to i-1, I delete array values from set if that exists in set, thus mex till i-1 can be obtained from set.begin(). Now at i-1, I insert 0 to mex-1 in set and repeat the set delete process till j. Now set begin will give mex(i,j).
Complexity won't change as those set insertions take extra mex number of operations for a segment i to j and array length covered in that segment is greater than equal to mex(i,j). So if you divide the array in some segments and each segment i has a size of ki then you are doing at max sum(2*ki) operations and as sum(ki)=array size, total number of operations are less than equal to 2*n. (For each segment with size ki, we need ki deletion and maximum ki insertion in the set)
Thanks, that was a great answer. I have understood all only just now. Your solution is very beatiful.
The complexity of your solution O(n * n * logn)
I am getting WA25 on My solution of D, Would some give me an example so I could understand, Thanks for helping in Advance
Failing test case
In Div 1A for test case -
1 3 1 1 1Why is answer
0 0 0wrong? According to the definition in problem statement0 0 0is larger than0. We can obtain0 0 0by choosingk=13 times.Upd: Nvm. Realized its correct answer. I did changed
breaktocontinuein my code before submitting..In Div2 D, I don't think it's enough to pair at most 2 strings. Consider the following example
z yxa xyzI don't see how we can select 2 strings to form palindrome, but selecting all surely works. What am I missing ?? Help me!
zis a plindorome. I am stupid.Please ignore.zis a palindromeI'm confused about the test data of problem E (div. 2). What I understood from the problem statement is "each cell contains the xor sum of all its adjacent cells". Suppose we have a grid of $$$2\times2$$$ like this:
The xor sum of neighboring cells for each cell will be:
So the conditions $$$y_{1,1} = y_{2, 2}$$$ and $$$y_{1,2} = y_{2,1}$$$ should be satisfied for a valid $$$2\times 2$$$ grid.
But why the test contains test data like this?
What is a possible original grid for this test data? Am I missing something?
In order to make sure the tests are actually obtainable as neighbor sums, we made the problem a "fake interactive". The tests are made as Victor's original grid, and then the interactor finds the neighbor sum before giving it to your solution.
When you look at the test cases on the submission page, you see Victor's original grid, not the neighbor sum.
Thanks for the clarification.
is there a DP-solution for problem D — div2 ?
No there is clearly no DP solution
However I can explain you my thought process which might help you ?
First you see that it's written in bold that strings are of length at most 3 so it must be really useful ! Usually this kind of stuff allows us to use pigeonhole principle or something like this.
Notice that if you have any string of length 1 then the problem is solved (it's in the samples)
Now, by trying very basic casework we see that it's obvious that if you have a string and it's reversed version, then you can answer yes.
This let's us with a very few number of strings...Indeed, the number of strings of size 3 in a set that has NO symmetrical strings is $$$\frac{26^3}{2}$$$
So we might use some sort of bruteforce (because we wouldn't have the special constraints over length of strings otherwise).
Now you might finally try to show that you can always get a palindrome using one string of length 2 and one string of length 3.
I hope it helped :p
yeah i understand! Thanks a lot * big heart *
Nice explanation..
For div 2E, you can visit each cell and include it in the xor if the neighbours haven't been marked. Initially all cells are unmarked. After including a cell mark all its neighbours, as they will be included in the xor.
Accepted solution
Wow, this solution is surprisingly simple, can you explain why this would works? Thanks.
It works because each cell contains xor of the neighbouring cells, and we need the xor of all elements, so we need to find a combination of cells that will include each element once or odd number of times. By trial and error I found out that there is always a combination possible which includes all cells once.
We can't include cells that share neighbours as those neighbours will be included twice and xor of a number with itself is 0.
For problem E . It seems that many problem requiring finding a path to any node in the tree can be turned into find the path to the ending nodes of "diameter" of the tree (the diameter here can be the sum of length,max ...). And the ending nodes of diameter can be easily maintain by segment tree.
I first saw this trick here : https://mirror.codeforces.com/contest/1434/problem/D
Can anyone explain how come the number of odd numbers in the range
[l,r]is given by(r-l+1)+(r/2+(l-1)/2)???r - l + 1is the number of numbers in[l, r]r / 2is the number of even numbers in[1, r](l - 1) / 2is the number of even numbers in[1, l - 1]so
(r / 2) - ((l - 1) / 2)is the number of even numbers in[l, r]subtracts the number of even numbers from the total number of numbers -> you get number of odd numbers
fun contest, thoroughly enjoyed the problems :D
Can anyone tell me what's the error in my implementation of problem D 143737471
Failing test case
thanks for the response
I think the 1628C — XOR-сетка method seems a little troublesome, I have a very concise writing here
Starting from the second row, you only need to select those cells that have been selected an even number of times in the previous row for XOR
My solution for Div1D:
Let $$$f(n, m)$$$ be $$$2^{n - 1}$$$ times the answer for $$$k=1$$$, so that this value is always an integer.
Note that we have the recurrence relation $$$f(n, m)=f(n - 1, m) + f(n - 1, m - 1),$$$ as well as the known values $$$f(n, n) = n\cdot 2^{n - 1}.$$$
Let $$$F(n, m)$$$ be the same function as $$$f$$$ but extended by the recurrence relation to values where $$$m > n$$$ (so $$$F(n - 1, n)=F(n, n) - F(n - 1, n - 1)$$$). We can compute $$$F(0, m) = m.$$$
We can easily use these values as a basis for computing $$$F(n, m)$$$ as a sum, as the value $$$F(0, m')$$$ will contribute to this $$$\binom n{m - m'}$$$ times.
Then $$$F(n, m)$$$ is just $$$\sum_{i=1}^m i\binom n{m - i},$$$ from which we can easily compute the desired answer.
Code: 143689440
Hey in the question 1628A - Meximum Array , can anyone explain the correctness of second test case as per the problem statement :
I think the second test case should be like this
2 2 3 4 0 1 2 0 -> [2 2 3 4 ] = 5
0 1 2 0 -> [0 1 2] = 3
0 -> [0] = 1
so vector b becomes [5,3,1] and this is lexicographically greater than the given b -> [5,3,1]
Kindly clarify this.
[2,2,3,4] mex will be 0
Explained 1628D1 — Game on Sum (Easy Version) DP Concept much clearly up here:
DP Concept Video Explaination
Can anyone check my solution for Div2 D? I can't find what's wrong here. https://mirror.codeforces.com/contest/1629/submission/143764101
Failing test case
oh I got it ! Thank u so much
How to solve Div2C/Div1A in o(n) ?
O(n) submission 143659611
There is a slightly easier solution for the Div1 C task. I noticed that if we suppose the table is chessboard, every cell would contain information only about the other color. So, we can calculate XOR of all the white and black cells separately. If left up cell is white, to calculate answer on the black cells, we simply need to go from the left up diagonal to the right down. To count every cells one time, we can use the previous diagonal and add cells as on the picture. (x is diagonal we want to count, 2 is diagonal we already know, 1 is for cells we need to take). Counting the answer for other diagonals is pretty similar.
Scheme: https://imgur.com/a/ut95K9y
My solution: https://mirror.codeforces.com/contest/1629/submission/143699683
Great Contest
For 2C.. What is the output for
I think the answer should be 4?
No, each element of the answer won't be append to the end of the array.
This is a much easier solution for Div1C, we can calculate the white cell in the same way.
I have a question about div2C (which is much harder than div2D btw). Let
mbe an array of MEX suffices. That is,m[i]is MEX of all elements froma[0]toa[i]. From this, how to calculate MEX of all elements froma[l]toa[r]for anylandr?I think you meant prefixes. I don't think we can calculate mex of a range using this information alone efficiently. For example, let mex of a[0] to a[l] be x and mex of a[0] to a[r] be y, then it could mean that a[l] to a[r] could contain some or none of the numbers in the range 0 to y-1, and depending on what numbers are present in a[0] to a[l], the mex of a[l] to a[r] could vary.
About the problem D1 (Div 1), what if $$$\frac{DP[i-1][j] - DP[i-1][j-1]}{2} > k$$$, in that case the optimal $$$x$$$ would be $$$x = k$$$, but the fact that we're working under $$$\mathbb{Z}_{10^9 + 7}$$$ makes impossible to identify this case. I would appreciate some explanation about this. I'm probably missing something.
It's always worse for Bob to be forced to add more. But how much worse? The difference between an add and a subtract cannot be more than $$$2k$$$, So the difference between $$$DP[i][j]$$$ and $$$DP[i][j-1]$$$ cannot be more than $$$2k$$$. One can also use induction to show that the optimal value of for Alice to pick is always in the range $$$[0, k]$$$.
True. Thank you.
can you please prove in detail how dp[i][j]-dp[i][j-1]<=2k ? magnus.hegdahl
How do we efficiently calculate the Mex for the Mex problem?
Store a bool list of whether you have seen some number or not. Start with saying the mex is 0, and then while you have seen the mex, increment it. But you must be careful about resetting this structure, since it involves a big list, and clearing the entire list might be slow if you need to do it many times. Therefore, you can keep another list of which numbers where actually changed, and then you only need to reset those.
I thought of something similar actually. I implemented it using a set, a counter variable, and a current MEX variable
Regarding the Editorial's solution for Div2E, I have wondered why does this strategy always work, I mean why do the $$$n^{th}$$$ row cells always get used odd number of times by the time the $$$(n-1)^{th}$$$ row cells get used odd number of times. After some thinking I reached the following proof:
Assume a matrix $$$mat$$$ such that $$$mat[i][j]$$$ is $$$1$$$ if we XOR the result with $$$xor\_sum[i][j]$$$ and $$$0$$$ otherwise. We want to prove that using a valid (every cell in the original grid is included odd number of times) matrix $$$mat$$$ of size $$$n\times (n-1)$$$ ($$$n$$$ is even) where the first and last rows are all ones, and the first and last column values from top to bottom are $$$1, 0, 1, 0, ..., 1, 0, 1$$$, we can always build another valid matrix $$$mat2$$$ of size $$$(n+8)\times (n+7)$$$.
Define boundary cells of a matrix of size $$$n\times m$$$ to be the cells with row $$$1$$$ or $$$n$$$ or column $$$1$$$ or $$$m$$$. Using matrix $$$mat$$$ of size $$$n\times (n-1)$$$, let's add new boundary cells in $$$4$$$ steps to reach our desired matrix $$$mat2$$$:
Observe how all the new rows/columns are added in a way such that their respective original grid cells are used odd number of times. The base cases are for $$$n = 2, 4, 6, 8$$$, using these we can build the matrix of any other even positive $$$n$$$.
To obtain the $$$n\times n$$$ matrix, simple append a first row of all zeros, its cells will be always valid (as the row below it is all ones) and will not affect the validity of other cells.
Example for obtaining $$$mat2$$$ of size $$$12\times 11$$$ from $$$mat$$$ of size $$$4\times 3$$$:
$$$mat$$$:
$$$mat2$$$ ($$$mat$$$ is highlighted in yellow):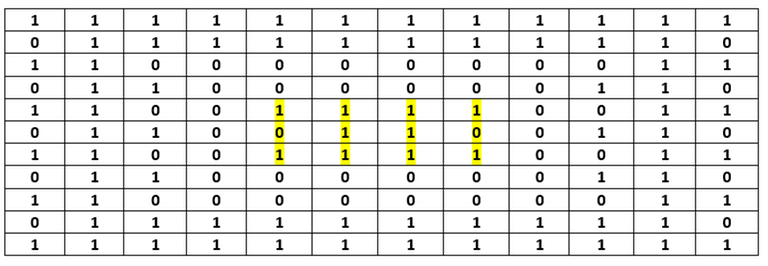
The binary tree, LCA stuff in the editorial of E are essentially proving this cool fact:
Let $$$f_T(x, y)$$$ be the maximum weight along the simple path from $$$x$$$ to $$$y$$$ in an edge-weighted tree $$$T$$$. Then, given any edge-weighted tree $$$T$$$, there exists a tree $$$T'$$$ such that $$$\forall x, y : f_T(x, y) = f_{T'}(x, y)$$$, and every vertex of $$$T'$$$ has degree $$$\leq 2$$$ (i.e. $$$T'$$$ is a line).
And here is how to construct $$$T'$$$ in $$$O(n\log n)$$$:
To solve problem E, just do the tree replacement, and then it reduces to an easy problem on an array. :)
Another problem that can be solved using this trick is 609E - Minimum spanning tree for each edge.
Another relevant problem: 1648E - Air Reform
You have changed test case 1 of E in judging but the answer is still the same as the test case 1 given in the question, pls correct it so my answer gets accepted.
It is not changed. The data shown on the submission page is Victor's original grid, not the data given to your solution. What your program reads will still be what you see as the sample in the statement.
In Div1 D1 how do we go from this statement
$$$DP[i][j]=min(DP[i−1][j−1]+x,DP[i−1][j]−x)$$$ for x that maximizes this value.
To this statement
$$$DP[i][j]=(DP[i−1][j−1]+DP[i−1][j])/2$$$
Shouldn't it be
$$$DP[i][j] = DP[i-1][j-1] + min(k, (DP[i-1][j] - DP[i-1][j-1])/2)$$$
because of the constraint on x?
Yes, but the difference between Bob adding and subtracting will never be greater than $$$2k$$$, so the $$$DP$$$ state with one fewer forced add will also not be more than $$$2k$$$ less than the other state.
I see, thanks!
Why we are taking MEX of SUFFIX not that of PREFIX ? Please explain. Thanks.
We precompute the mex of the suffix because we always want to take a big enough prefix that the mex is equal to the mex of the rest of the array. The rest of the array is some suffix.
I have the same idea on problem C, but I don't know how to find MEX on subsegment. Can you explain?
What I have done is that, took the frequency of every element of an array , and then for calculating MEX 'simply check the lowest element in frequency array whose count is 0'. This will we your 1st MEX element of the res array. For finding rest MEX elements I iterate over every element. Meanwhile I also maintain a flag array and the pointer named 'ptr'. flag array only check whether the element below the MEX are present or not, while ptr check whether all the elements which are below MEX occurred or not (if occurred than resizing the flag array).
Updating this, Now I'm able to passed the 2nd test case but on test case 6 WA occurred. If you are able to figure out than please help me.
I couldn't find bug in your code, but solution is too slow.
I did like this :
I had cnt[], which calculated count of elements, and find the mex on suffix and subsegment with it.
You can check my code : https://mirror.codeforces.com/contest/1628/submission/143904740
can anyone tell me why my solution for problem D is not working https://mirror.codeforces.com/contest/1629/submission/143927718
hey i dont exactly know what testcase ur failing on but i can give u a couple examples
2
plr
lp
(plrlp is obv a palindrome, and ur code doesnt check that.)
another one being
2
sf
sfo
(you can't make a palindrome from these but your code returns yes.)
as for fixing this, id take a look at how ur inserting into your map, as bc sometimes u insert the original string, and sometimes you insert the reverse. prob just normalize it into only inserting reverse or only inserting the original. additionally some cases where str1 is len 2 and str2 is len 3 u fail on. the situation where the len 2 string comes before works fine in ur code, like sf ofs, but when it comes after you dont check it. hope this helps :3
thanks for replying now i can correct my solution
For Problem-E (Div.2),
Another logic would be to do
ans = ans ^ grid[i][j]for alli and j within bounds(0 <= i, j < n) iff all neighbours of grid[i][j] are still unvisited (here grid refers to the grid which is given in input). In this way we guarantee that every element of Victor's actual grid is counted only once while taking xor.This has been stress tested by harasees_singh for all
even nfrom2 to 1000.Here is the link to my submission: 143698533
Can anyone help me with my submission of D of Div2.
problem-1628B - Peculiar Movie Preferences My submission-143689113 Thank you
Here's another solution for Div1E, which uses the following observation:
Let $$$A$$$ be any subset of vertices, $$$a_i$$$ be the $$$i$$$-th element of $$$A$$$, $$$f(x,y)$$$ be the maximum edge weight on the unique path from $$$x$$$ to $$$y$$$, and $$$p$$$ be any permutation of $$$[|A|]$$$.
Then the following holds:
That is, the maximum edge weight on any path from two elements of $$$A$$$ is the maximum of $$$f(a_i,a_{i+1})$$$ of any ordering of $$$a$$$.
Proof: It's sufficient to show that any edge which is on at least one path of a pair of vertices from $$$A$$$ will be on at least one of the paths $$$(a_i,a_{i+1})$$$. Let's take any such edge. Then the vertices of $$$A$$$ can be split into two subsets $$$A_1$$$ and $$$A_2$$$ based on which side of the edge they are on. It's easy to see that as long as neither of the two subsets is empty, any ordering of $$$a$$$ will contain two consecutive elements, such that one is from $$$A_1$$$ and the other is from $$$A_2$$$. $$$\square$$$
To solve the problem, first notice that if $$$B$$$ is the current set of vertices that are on, and $$$c$$$ is the query vertex, we are looking for $$$\max\limits_{x \in B \cup\{c\}}\max\limits_{y \in B \cup\{c\}}f(x,y)$$$.
Since any ordering works, let's simply take the ordering from the input. Then we can preprocess $$$f(i,i+1)$$$, make a segment tree keeping $$$f(x,y)$$$ of consecutive elements of $$$B$$$, and notice that any update requires the addition of at most two $$$f(x,y)$$$ calls that weren't already preprocessed. This gives an $$$\mathcal{O}(n \log n)$$$ solution. Code: 144633280.
thanks very much for sovle, it 's very useful for me
Could anyone please explain why my O(n*logn*logn) for problem C is giving TLE?
My submission link: https://mirror.codeforces.com/contest/1629/submission/238484131