Well, As my friends sent me some screenshots from his messages, I am now sure that he is one of the new big cheaters in codeforces, sailikpandey, I've warned him many times in DM in Cf but he didn't care now I think it's time to share the proofs :

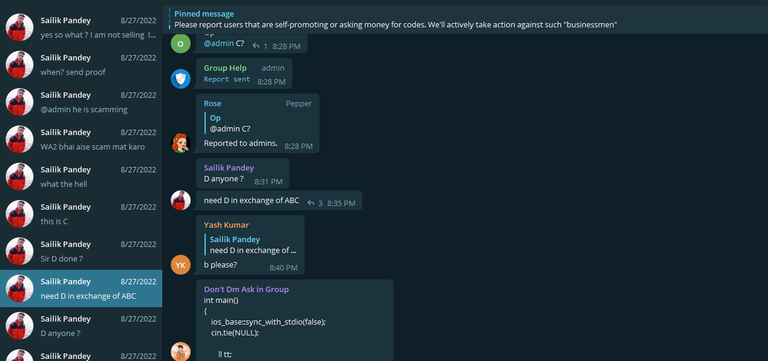
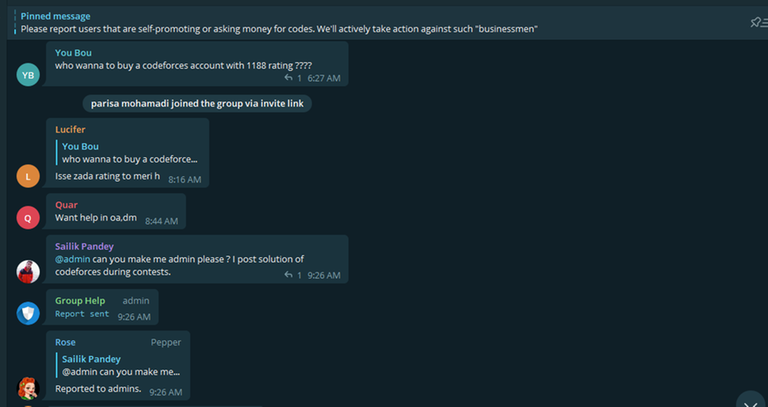
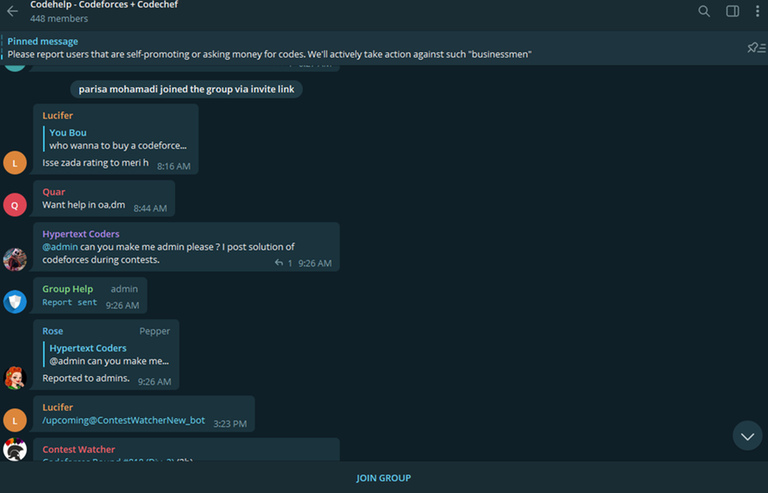
Also immediately after receiving my messages and not accepting that he is a cheater, He changed his username on Telegram as you can see the difference in the last picture and the picture below :

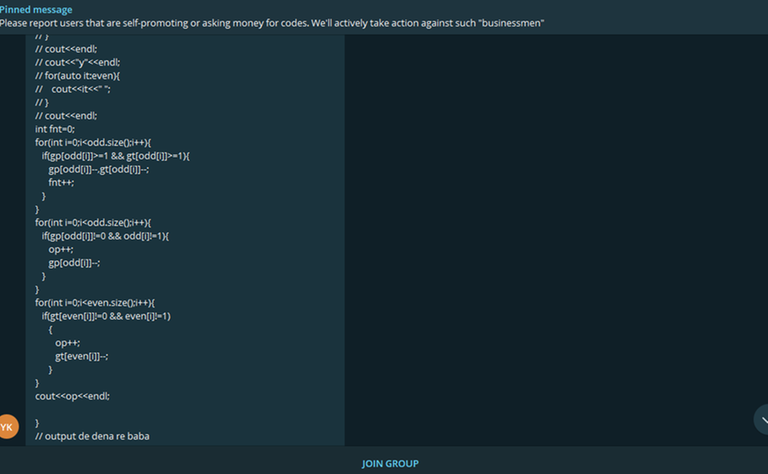
His strategy is writing many comments that makes the code unreadable, And when I asked him why you do this he says it's because to make hackers not able to read my code but as you can see this is the code which has been revealed in the group last night for Edu 135 problem C (Which is a very bad thing) :

And this is his submission : 171412386

If you compare his code with the given in screenshot you see no difference, Also All of his contests submissions contains heavy and many comments which is a violation of codeforces rules, Please Mike or other people if you can do sth to stop such cheaters, Thanks, MikeMirzayanov

P.S : Congrats cheater, You became specialist sailikpandey :)

Google-forces round 810 :

• Problem C div1

• Problem E div1

Google-forces round 808 :

• Problem D div2

Google-forces round 805 :

• Problem G

• Problem F

This shows nowadays we need to learn Chinese language and improve our searching skills, But this isn't fair, MikeMirzayanov What's your opinion about this?

P.S : Every single thing I say in the comments is just my opinion and never wanna insult any country/organization/person and etc.

You are given a number $$$n$$$, And we have two functions, We declare $$$P(S)$$$ for a set of numbers, product of all the numbers in the set, Also we declare $$$F(S)$$$ for a set of numbers, sum of all the numbers in the set, You have the set {$$$1, 2, 3, ... , n$$$} you have to calculate

for all non empty subsequences of {$$$1, 2, 3, ... , n$$$}, in the other words you have to provide a solution that calculates sum of $$$F(S)/P(S)$$$ for all non empty subsequences.

For example the answer for $$$n = 2$$$ is this :

• for {$$$1$$$} sum is $$$1$$$ and product of numbers in it is $$$1$$$ so $$$F($$${$$$1$$$}$$$)/P($$${$$$1$$$}$$$)$$$ is $$$1/1 = 1$$$

• for {$$$2$$$} sum is $$$2$$$ and product of numbers in it is $$$2$$$ so $$$F($$${$$$2$$$}$$$)/P($$${$$$2$$$}$$$)$$$ is $$$2/2 = 1$$$

• and for the last non empty subsequence {$$$1, 2$$$} sum is $$$3$$$ and product of the numbers in it is $$$2$$$ so $$$F($$${$$$1, 2$$$}$$$)/P($$${$$$1, 2$$$}$$$)$$$ is $$$3/2 = 1.5$$$

So the answer for $$$n = 2$$$ is $$$1 + 1 + 1.5 = 3.5$$$

Constraints :

$$$1 \le n \le 10^6$$$

Hope you enjoy the problem, I'll share my approach's proof after $$$24$$$ hours!

Hello, The main reason of newbies' fear from XOR is bad reference in the problem statements to explain XOR and other bitwise operations (Authors usually put Wikipedia reference) and newbies mostly can't understand what's XOR, today I wanna explain something about bitwise operations for this group of coders with simple language :

1- Bitwise OR :

In this operation the system compares bits in same index in binary representation and if at least one of the bits was $$$1$$$ it returns $$$1$$$ otherwise $$$0$$$, Also it is written as | in C++.

For example :

• Bitwise OR of $$$6$$$ and $$$3$$$ is :

• $$$6 = 110$$$ in binary representation and $$$3 = 011$$$.

• $$$6$$$ | $$$3 = 7 = (110$$$ | $$$011 = 111)$$$

• Note : If in any index a number doesn't have enough bits system supposes that there's a $$$0$$$ bit in that index in binary representation of that number.

2- Bitwise AND :

As it's guessable from it's name if all bits in same index were $$$1$$$ system return $$$1$$$ otherwise $$$0$$$, Also it's written as & in C++.

For example :

• Bitwise AND of $$$10$$$ and $$$3$$$ is :

• $$$10 = 1001$$$ and $$$3 = 0011$$$

• $$$10$$$ & $$$3 = 1 = 1001$$$ & $$$0011 = 0001$$$.

3- Bitwise XOR :

In this operation system compares bits in same index and if odd number of them were $$$1$$$ it returns $$$1$$$ otherwise $$$0$$$, Also it is written as xor or ^ in C++.

For example :

• Bitwise XOR of $$$3$$$ and $$$5$$$ and $$$8$$$ is :

• $$$8 = 1000, 5 = 0101, 3 = 0011$$$.

• $$$8$$$ ^ $$$5$$$ ^ $$$3 = 14 = 1000$$$ ^ $$$0101$$$ ^ $$$0011 = 1110$$$.

I hope it would be helpful for you 💗 💗 (BTW if you noticed any typo let me know).

PS : As people say in the comments I've added some educational problems about this topic, If you had problems about this topic please write down in the comments Thanks.