Hi,
I've tried downloading testcases of BOI 2015 problems from the contest's website. However downloading 3 of 6 problems(EDI, NET, TUG) testdata results in 404 Not found error.
Is there anyone who has access to the testdata of these problems? Could you please share them here?
Thanks.









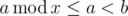 .
.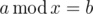 then
then 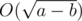 .
.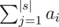 .
.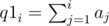
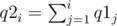
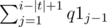 which is equal to
which is equal to 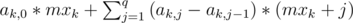 .
. 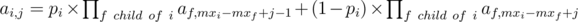 . Using this formula we can calculate
. Using this formula we can calculate 
