Tutorial is loading...
Code
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
scanf("%d", &n);
vector<int> a(n);
long long sum = 0;
for (int & x : a) {
scanf("%d", &x);
sum += x;
}
if (sum != 0) {
puts("YES");
puts("1");
printf("%d %d\n", 1, n);
exit(0);
}
sum = 0;
for (int i = 0; i < n; i++) {
sum += a[i];
if (sum != 0) {
puts("YES");
puts("2");
printf("%d %d\n", 1, i + 1);
printf("%d %d\n", i + 2, n);
exit(0);
}
}
puts("NO");
}
Tutorial is loading...
Code
#include <bits/stdc++.h>
using namespace std;
int main() {
char str[4][4 + 1];
// cells are '.', 'o', 'x'
for (int i = 0; i < 4; i++) {
cin >> str[i];
}
auto check = [&]() {
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
for (int dx = -1; dx <= 1; dx++) {
for (int dy = -1; dy <= 1; dy++) {
if (dx == 0 && dy == 0) continue;
if (i + dx * 3 > 4 || j + dy * 3 > 4 || i + dx * 3 < -1 || j + dy * 3 < -1) continue;
bool ok = true;
for (int p = 0; p < 3; p++) {
ok &= str[i + p * dx][j + p * dy] == 'x';
}
if (ok) return true;
}
}
}
}
return false;
};
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
if (str[i][j] == '.') {
str[i][j] = 'x';
if (check()) {
puts("YES");
exit(0);
}
str[i][j] = '.';
}
}
}
puts("NO");
}
Tutorial is loading...
Code
#include <bits/stdc++.h>
using namespace std;
#define all(x) (x).begin(), (x).end()
void solve() {
int n;
cin >> n;
vector<string> names(n);
for (string& name : names) {
cin >> name;
}
sort(all(names));
auto getIdx = [&](const string& s) {
int pos = lower_bound(all(names), s) - names.begin();
if (pos == (int)names.size() || names[pos] != s) return -1;
return pos;
};
auto splitIntoUserMessage = [](const string& s) {
size_t pos = s.find(':');
assert(pos != string::npos);
return make_pair(s.substr(0, pos), s.substr(pos + 1));
};
auto splitIntoTokensOfLatinLetters = [](const string& s) {
vector<string> result;
string token;
for (char c : s) {
if (isalpha(c) || isdigit(c)) {
token += c;
}
else {
if (!token.empty()) {
result.push_back(token);
}
token.clear();
}
}
if (!token.empty()) {
result.push_back(token);
}
return result;
};
int m;
cin >> m;
vector<int> who(m);
vector<vector<char>> can(m, vector<char>(n, true));
vector<string> messages(m);
string tmp;
getline(cin, tmp);
for (int i = 0; i < m; i++) {
string cur;
getline(cin, cur);
pair<string, string> p = splitIntoUserMessage(cur);
const string& user = p.first;
const string& message = p.second;
who[i] = getIdx(user);
if (who[i] != -1) {
fill(all(can[i]), false);
can[i][who[i]] = true;
}
messages[i] = message;
vector<string> tokens = splitIntoTokensOfLatinLetters(message);
for (const string& z : tokens) {
int idx = getIdx(z);
if (idx != -1) {
can[i][idx] = false;
}
}
}
vector<vector<int>> par(m, vector<int>(n, -1));
for (int i = 0; i < n; i++) {
if (can[0][i]) par[0][i] = 0;
}
for (int msg = 0; msg + 1 < m; msg++) {
for (int i = 0; i < n; i++) {
if (par[msg][i] == -1) continue;
for (int j = 0; j < n; j++) {
if (i == j) continue;
if (can[msg + 1][j]) {
par[msg + 1][j] = i;
}
}
}
}
int msg = m - 1, pos = -1;
for (int i = 0; i < n; i++) {
if (par[msg][i] != -1) {
pos = i;
break;
}
}
if (pos == -1) {
cout << "Impossible\n";
return;
}
while (msg >= 0) {
who[msg] = pos;
pos = par[msg][pos];
msg--;
}
for (int i = 0; i < m; i++) {
cout << names[who[i]] << ":" << messages[i] << "\n";
}
return;
}
int main() {
//freopen("input.txt", "r", stdin);
int t;
cin >> t; // number of tests
while (t--) {
solve();
}
}
Tutorial is loading...
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int nextInt() {
int x = 0, p = 1;
char c;
do {
c = getchar();
} while (c <= 32);
if (c == '-') {
p = -1;
c = getchar();
}
while (c >= '0' && c <= '9') {
x = x * 10 + c - '0';
c = getchar();
}
return x * p;
}
#define all(x) (x).begin(), (x).end()
const int N = (int)3e5 + 5;
const int MAX_VAL = (int)1e9;
int n;
ll l[N], r[N];
struct event {
ll x;
int c;
event() {}
event(ll x, int c) : x(x), c(c) {}
};
pair<ll, int> check(ll len) {
if (len == 0) return make_pair(0LL, n);
static vector<event> evs;
evs.resize(0);
for (int i = 1; i <= n; i++) {
if (r[i] - len > l[i]) {
evs.push_back(event(l[i], 1));
evs.push_back(event(r[i] - len, -1));
}
}
sort(all(evs), [](const event & a, const event & b) { return a.x < b.x; });
reverse(all(evs));
int cnt = 0, maxiCnt = 0;
ll bestPos = 0;
while (evs.size() > 0) {
ll x = evs.back().x;
while (evs.size() > 0 && evs.back().x == x) {
cnt += evs.back().c;
evs.pop_back();
}
if (cnt > maxiCnt) {
maxiCnt = cnt;
bestPos = x;
}
}
return make_pair(bestPos, maxiCnt);
}
vector<int> getAns(ll len) {
if (len == 0) {
vector<int> res(n);
iota(all(res), 1);
return res;
}
ll pos = check(len).first;
vector<int> res;
for (int i = 1; i <= n; i++) {
if (pos >= l[i] && pos < r[i] - len) {
res.push_back(i);
}
}
return res;
}
int main() {
n = nextInt();
int k = nextInt();
for (int i = 1; i <= n; i++) {
l[i] = nextInt();
r[i] = nextInt() + 2;
}
ll l = 0, r = MAX_VAL + MAX_VAL + 5;
while (r - l > 1) {
ll mid = (l + r) >> 1;
if (check(mid).second >= k) l = mid;
else r = mid;
}
vector<int> ans = getAns(l);
cout << l << endl;
assert((int)ans.size() >= k);
ans.resize(k);
for (int i : ans) {
printf("%d ", i);
}
puts("");
}
Tutorial is loading...
C++ code
#include <bits/stdc++.h>
using namespace std;
const int N = (int)404;
const int ALPHA = 26;
bitset<N> b[ALPHA][N];
char patt[N][N];
bitset<N> result[N];
bitset<N> getShifted(const bitset<N>& b, int len, int shift) {
assert(0 <= shift && shift < len);
return (b >> shift) | (b << (len - shift));
}
int main() {
#ifdef LOCAL
freopen("input.txt", "r", stdin);
#endif
int n, m, r, c;
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i++) {
static char str[N];
scanf("%s", str);
for (int j = 0; j < m; j++) {
b[(int)(str[j] - 'a')][i][j] = true;
}
}
scanf("%d%d", &r, &c);
for (int i = 0; i < n; i++) {
result[i] = ~result[i];
}
for (int i = 0; i < r; i++) {
scanf("%s", patt[i]);
for (int j = 0; j < c; j++) {
if (patt[i][j] == '?') continue;
int c = patt[i][j] - 'a';
int shiftByX = (((-i) % n) + n) % n;
int shiftByY = (((j) % m) + m) % m;
for (int x = 0; x < n; x++) {
int nx = (x + shiftByX);
if (nx >= n) nx -= n;
result[nx] &= getShifted(b[c][x], m, shiftByY);
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
putchar(result[i][j] ? '1' : '0');
}
puts("");
}
}
Java code
import java.io.*;
import java.util.*;
public class Main {
static class InputReader {
BufferedReader bufferedReader;
StringTokenizer stringTokenizer;
InputReader(InputStream inputStream) {
bufferedReader = new BufferedReader(new InputStreamReader(inputStream), 32768);
stringTokenizer = null;
}
String next() {
while (stringTokenizer == null || !stringTokenizer.hasMoreTokens()) {
try {
stringTokenizer = new StringTokenizer(bufferedReader.readLine());
} catch (IOException ex) {
ex.printStackTrace();
throw new RuntimeException(ex);
}
}
return stringTokenizer.nextToken();
}
int nextInt() {
return Integer.parseInt(next());
}
long nextLong() {
return Long.parseLong(next());
}
double nextDouble() {
return Double.parseDouble(next());
}
}
static int[] newBitSet(int n) {
return new int[(n + 31) / 32];
}
static void setBit(int[] a, int pos) {
a[pos >>> 5] |= (1 << (pos & 31));
}
static boolean getBit(int[] a, int pos) {
return ((a[pos >>> 5]) & (1 << (pos & 31))) != 0;
}
static void setAll(int[] a) {
for (int i = 0; i < a.length; i++) {
a[i] = ~0;
}
}
static void resetAll(int[] a) {
for (int i = 0; i < a.length; i++) {
a[i] = 0;
}
}
static void andXYtoX(int[] x, int[] y) {
for (int i = 0; i < x.length; i++) {
x[i] &= y[i];
}
}
static void leftShiftAndOr(int ch, int shift, int x, int[][][][] shl, int[] to) {
int[] z = shl[ch][shift & 31][x];
int delta = (shift >>> 5);
for (int i = delta; i < to.length; i++) {
to[i - delta] |= z[i];
}
}
static void rightShiftAndOr(int ch, int shift, int x, int[][][][] shr, int[] to) {
int[] z = shr[ch][shift & 31][x];
int delta = (shift >>> 5);
for (int i = 0; i + delta < to.length; i++) {
to[i + delta] |= z[i];
}
}
static void printBitset(int a[], int l, int r) {
for (int i = l; i <= r; i++) {
System.err.print(getBit(a, i) ? '1' : '0');
}
System.err.println();
}
static final int ALPHA = 26;
public static void main(String[] args) {
InputReader in = new InputReader(System.in);
PrintWriter out = new PrintWriter(System.out);
int n = in.nextInt();
int m = in.nextInt();
int[][][][] shl = new int[ALPHA][32][n][];
int[][][][] shr = new int[ALPHA][32][n][];
for (int c = 0; c < ALPHA; c++) {
for (int sh = 0; sh < 32; sh++) {
for (int i = 0; i < n; i++) {
shl[c][sh][i] = newBitSet(m);
shr[c][sh][i] = newBitSet(m);
}
}
}
String[] s = new String[n];
for (int i = 0; i < n; i++) {
s[i] = in.next();
for (int j = 0; j < m; j++) {
int c = s[i].charAt(j) - 'a';
for (int sh = 0; sh < 32; sh++) {
if (j - sh >= 0) {
setBit(shl[c][sh][i], j - sh);
}
if (j + sh < m) {
setBit(shr[c][sh][i], j + sh);
}
}
}
}
int r = in.nextInt();
int c = in.nextInt();
String[] patt = new String[r];
int[][] res = new int[n][];
for (int i = 0; i < n; i++) {
res[i] = newBitSet(m);
setAll(res[i]);
}
int[] tmp = newBitSet(m);
for (int i = 0; i < r; i++) {
patt[i] = in.next();
for (int j = 0; j < c; j++) {
if (patt[i].charAt(j) == '?') continue;
int cur = patt[i].charAt(j) - 'a';
int shiftByX = (((-i) % n) + n) % n;
int shiftByY = (((j) % m) + m) % m;
for (int x = 0; x < n; x++) {
int nx = x + shiftByX;
if (nx >= n) nx -= n;
resetAll(tmp);
leftShiftAndOr(cur, shiftByY, x, shl, tmp);
rightShiftAndOr(cur, m - shiftByY, x, shr, tmp);
andXYtoX(res[nx], tmp);
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
out.print(getBit(res[i], j) ? '1' : '0');
}
out.println();
}
out.close();
}
}









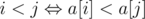 , так как числа в массиве
, так как числа в массиве 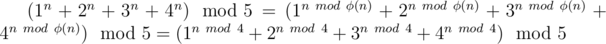
 .
.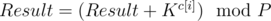 ,
, 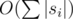 .
.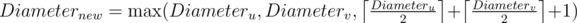
 блоков. В каждом блоке будем хранить сами числа в таком порядке, как в массиве
блоков. В каждом блоке будем хранить сами числа в таком порядке, как в массиве 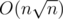 памяти.
памяти. операций. А потом уже вставить это же число тоже можем за
операций. А потом уже вставить это же число тоже можем за 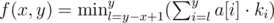 , где
, где 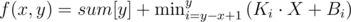 , где
, где  памяти. А запрос будет выполняться за
памяти. А запрос будет выполняться за 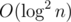 операций. Так как мы посетим
операций. Так как мы посетим  вершин и в каждой вершине выполним
вершин и в каждой вершине выполним 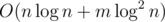 .
.
