Problem Statement:
You are given an array arr of size $$$N$$$. Initially, all $$$arr[i]$$$ are set to 0. Now consider $$$Q$$$ queries, where each query is of one of the following two types:
- [1, l, r]: In this case, calculate the sum of values of $$$arr[i]$$$ for $$$l \le i \le r$$$.
- [2, l, r, x]: In this case, for each $$$arr[i]$$$, $$$l \le i \le r$$$, update the value to $$$arr[i] = arr[i] \oplus x$$$ (where $$$\oplus$$$ is the XOR operation).
Constraints:
- $$$ 1 \le N \le 10^5 $$$
- $$$ 1 \le Q \le 10^5 $$$
- $$$ 1 \le l \le r \le N $$$
- $$$ 1 \le x \le 2^{30} - 1 $$$
Problem Link — 242E - XOR on Segment
Approach:
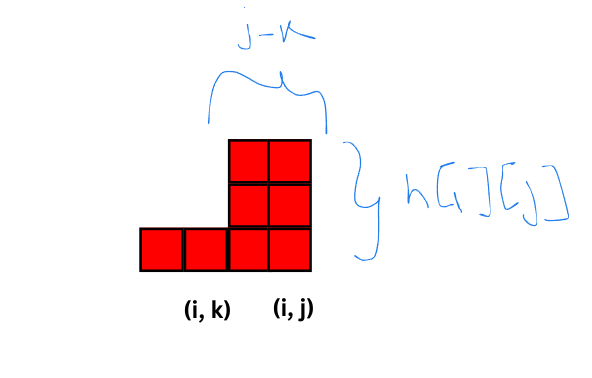
This problem can be solved easily with a Segment Tree with Lazy Propagation, had there been no XOR updates. Lazy Propagation requires that for an update on range $$$[l, r]$$$, we should be able to calculate the value of $$$[l, r]$$$ after the update in $$$O(1)$$$ time (or at least sub-linear time like $$$O(\log n)$$$).
For other updates, say multiply by $$$x$$$, this would be simple. The value of $$$[l, r]$$$ after the update would be:
new_sum = x * prev_sum
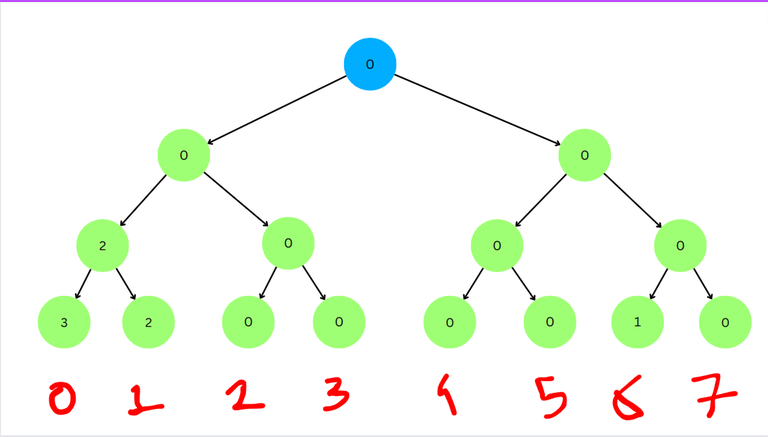
For XOR updates, though, this is not so straightforward.