Sometimes I wonder, what implementation of a segment tree to use. Usually, I handwave that some will suit, and that works in most of the cases.

But today I decided to back up the choice with some data and I ran benchmarks against 4 implementations:

• Simple recursive divide-and-conquer implementation
  Code

  struct SimpleRecursiveSegmentTree {
      unsigned size;
  
    private:
      std::vector<long long> t;
  
      void _build(const std::vector<int> &v, unsigned p, unsigned l, unsigned r) {
          if (r == l + 1) {
              t[p] = v[l];
              return;
          }
          unsigned m = (l + r) / 2;
          _build(v, 2 * p + 1, l, m);
          _build(v, 2 * p + 2, m, r);
          t[p] = t[2 * p + 1] + t[2 * p + 2];
      }
  
      long long _get(unsigned p, unsigned l, unsigned r, unsigned a,
                     unsigned b) const {
          if (b <= l || r <= a) {
              return 0LL;
          }
          if (a <= l && r <= b) {
              return t[p];
          }
          unsigned m = (l + r) / 2;
          return _get(2 * p + 1, l, m, a, b) + _get(2 * p + 2, m, r, a, b);
      }
  
      void _add(unsigned p, unsigned l, unsigned r, unsigned i, int x) {
          if (i < l || r <= i) {
              return;
          }
          if (r == l + 1) {
              t[p] += x;
              return;
          }
          unsigned m = (l + r) / 2;
          _add(2 * p + 1, l, m, i, x);
          _add(2 * p + 2, m, r, i, x);
          t[p] = t[2 * p + 1] + t[2 * p + 2];
      }
  
    public:
      SimpleRecursiveSegmentTree(unsigned _size) noexcept : size(_size) {
          t.resize(4 * size);
      }
  
      SimpleRecursiveSegmentTree(const std::vector<int> &v) noexcept
          : size(v.size()) {
          t.resize(4 * size);
          _build(v, 0, 0, size);
      }
  
      void add(unsigned i, int x) { _add(0, 0, size, i, x); }
  
      long long get(unsigned l, unsigned r) const {
          return _get(0, 0, size, l, r);
      }
  };
  

• Optimized recursive divide-and-conquer, which does not descend into apriori useless branches
  Code

  struct OptimizedRecursiveSegmentTree {
      unsigned size;
  
    private:
      std::vector<long long> t;
  
      void _build(const std::vector<int> &v, unsigned p, unsigned l, unsigned r) {
          if (r == l + 1) {
              t[p] = v[l];
              return;
          }
          unsigned m = (l + r) / 2;
          _build(v, 2 * p + 1, l, m);
          _build(v, 2 * p + 2, m, r);
          t[p] = t[2 * p + 1] + t[2 * p + 2];
      }
  
      long long _get(unsigned p, unsigned l, unsigned r, unsigned a,
                     unsigned b) const {
          if (a <= l && r <= b) {
              return t[p];
          }
          unsigned m = (l + r) / 2;
          long long res = 0;
          if (a < m) {
              res += _get(2 * p + 1, l, m, a, b);
          }
          if (b > m) {
              res += _get(2 * p + 2, m, r, a, b);
          }
          return res;
      }
  
      void _add(unsigned p, unsigned l, unsigned r, unsigned i, int x) {
          if (r == l + 1) {
              t[p] += x;
              return;
          }
          unsigned m = (l + r) / 2;
          if (i < m) {
              _add(2 * p + 1, l, m, i, x);
          } else {
              _add(2 * p + 2, m, r, i, x);
          }
          t[p] = t[2 * p + 1] + t[2 * p + 2];
      }
  
    public:
      OptimizedRecursiveSegmentTree(unsigned _size) noexcept : size(_size) {
          t.resize(4 * size);
      }
  
      OptimizedRecursiveSegmentTree(const std::vector<int> &v) noexcept
          : size(v.size()) {
          t.resize(4 * size);
          _build(v, 0, 0, size);
      }
  
      void add(unsigned i, int x) { _add(0, 0, size, i, x); }
  
      long long get(unsigned l, unsigned r) const {
          return _get(0, 0, size, l, r);
      }
  };
  

• Non-recursive implementation (credits: https://mirror.codeforces.com/blog/entry/18051)
  Code

  struct NonRecursiveSegmentTree {
      unsigned size;
  
    private:
      std::vector<long long> t;
  
      void _build(const std::vector<int> &v) {
          std::copy(v.begin(), v.end(), t.begin() + size);
          for (int i = size - 1; i > 0; --i) {
              t[i] = t[i * 2] + t[i * 2 ^ 1];
          }
      }
  
    public:
      NonRecursiveSegmentTree(unsigned _size) noexcept : size(_size) {
          t.resize(2 * size);
      }
  
      NonRecursiveSegmentTree(const std::vector<int> &v) noexcept
          : size(v.size()) {
          t.resize(2 * size);
          _build(v);
      }
  
      void add(unsigned i, int x) {
          i += size;
          for (t[i] += x; i > 1; i /= 2) {
              t[i / 2] = t[i] + t[i ^ 1];
          }
      }
  
      long long get(unsigned l, unsigned r) const {
          long long res = 0;
          for (l += size, r += size; l < r; l /= 2, r /= 2) {
              if (l & 1) {
                  res += t[l++];
              }
              if (r & 1) {
                  res += t[--r];
              }
          }
          return res;
      }
  };
  

• Fenwick Tree
  Code

  struct FenwickTree {
      unsigned size;
  
    private:
      std::vector<long long> t;
  
      long long get_prefix(int i) const {
          long long res = 0;
          while (i >= 0) {
              res += t[i];
              i = (i & (i + 1)) - 1;
          }
          return res;
      }
  
    public:
      void add(unsigned i, int x) {
          while (i < size) {
              t[i] += x;
              i = i | (i + 1);
          }
      }
  
      FenwickTree(unsigned _size) : size(_size) { t.resize(size); }
  
      FenwickTree(const std::vector<int> &v) : size(v.size()) {
          t.resize(size);
          for (unsigned i = 0; i < size; ++i) {
              add(i, v[i]);
          }
      }
  
      long long get(unsigned l, unsigned r) {
          return get_prefix((int)r - 1) - get_prefix((int)l - 1);
      }
  };
  

All implementations are able to:

• get(l, r): get sum on a segment (half-interval) $$$[l; r)$$$
• add(i, x): add $$$x$$$ to the element by index $$$i$$$

Here are the results: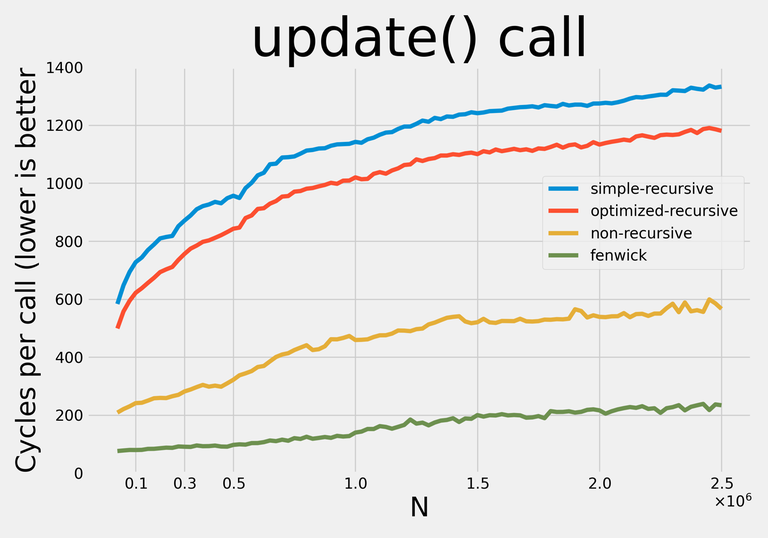

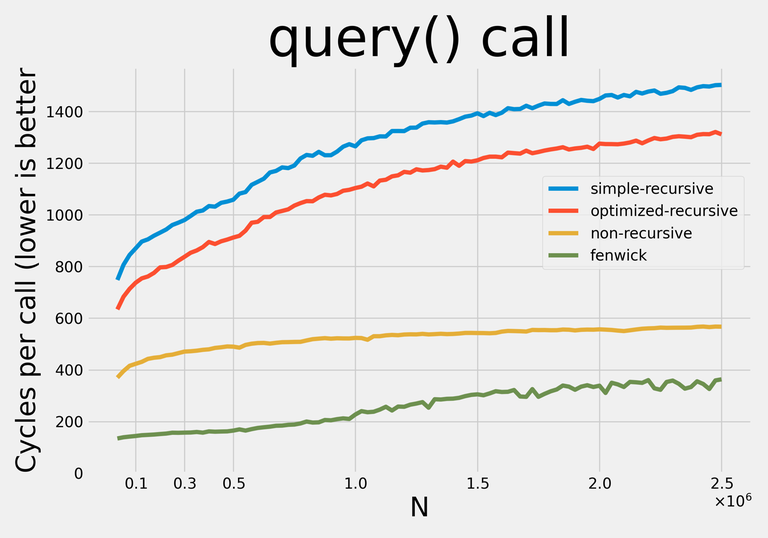
Note: I decided not to apply any addition-specific optimizations so that with minor modifications the data structures could be used for any supported operations.

I generated queries the following way:

• Update: generate random index (rnd() % size) and number
• Query: at first, generate random length (rnd() % size + 1), then generate a left border for that length

Benchmarking source code. Note that ideally you should disable frequency scaling, close any applications that might disrupt the benchmark (basically, the more you close — the better) and pin the benchmark process to a single CPU (core).

Plot-generating Python script

My benchmarking data in case you want to do some more plotting/comparing.

I compiled the benchmark with #pragma GCC optimize("O3") on GNU GCC 11.3.0, and ran it with the CPU fixed on 2.4 GHz, the process pinned on a single CPU core and the desktop environment closed.

This is probably my first useful contribution so any suggestions/improvements are welcome.