В этой задаче требовалось сделать то, что написано в условии. Считать числа и определить у кого из ребят больше баллов.
Асимптотика: O(1).
Для начала немного переформулируем задачу. Был дан ориентированный граф, вершинами которого являются хэндлы пользователей, а ребрами запросы изменения хэндлов. Он состоит из некоторого количества цепочек, нужно было найти их количество, начальные и конечные вершины каждой цепочки. То есть у каждой вершины входящая и исходящая степень не превосходит 1. Ввиду последнего ограничения, ребра этого графа можно хранить в словаре(в C++ — std::map\unoredered_map, Java — TreeMap\HashMap), где ключом является вершина из которой исходит ребро, а значением — вершина, в которую оно входит.
Каждому уникальному пользователю соответствует вершина с нулевой входящей степенью. Из всех таких вершин нужно переходить по ребру, до тех пор, пока существует переход. Чтобы найти вершины с нулевой степенью, запомним вершины в которые входит ребро, и добавим их в множество(в C++ — std::set\unoredered_set, Java — TreeSet\HashSet).
Асимптотика: 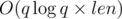 .
.
Заметим, что у непустого леса найдется вершина со степенью 1(такая вершина называется листом). Будем удалять ребра графа по очереди и поддерживать актуальные значения (degreev, sv), до тех пор пока он не станет пустым. Для этого будем поддерживать очередь(или стек) вершин являющихся листьями. На очередной итерации мы достаем вершину v из очереди, и удаляем ребро (v, sv), для этого делаем degreesv -= 1 и ssv ^= v. Если у вершины sv степень стала равной 1, то добавим ее в очередь.
Необходимо обработать случай, когда мы достаем вершину v из очереди и у нее degreev = 0, тогда стоит проигнорировать это, так как мы уже удалили нужное ребро.
Асимптотика: O(n)
504B - Миша и сложение перестановок
Для решения данной задачи необходимо научиться находить порядковый номер данной перестановки и перестановку по данному порядковому номеру. Так порядковые номера имеют достаточно большую длину, будем хранить их в факториальной системе счисления. То есть число x будем представлять как 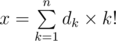 .
.
Чтобы найти порядковый номер перестановки, заменим каждое число в перестановке на количество чисел стоящих правее и меньше его. Таким образом мы получим число, записанное в факториальной системе счисления.
Чтобы получить по порядковому номеру перестановку необходимо провести обратную процедуру, для этого потребуется находить k-тое по величине число в множестве, и добавлять элемент в множество. В обоих случаях нам пригодится дерево отрезков, которое позволяет отвечать на запросы такого вида.
В итоге получаем, что нам необходимо получить индексы перестановок, сложить их в факториальной системе счисления по модулю n!, и провести обратное преобразование. Для лучшего понимания ознакомьтесь с wiki и/или любым прошедшим решением.
Асимптотика:  или
или 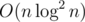 .
.
Заметим, что если количество элементов, встречающихся нечетное число раз, больше одного — ответ равен нулю. Аналогично, если массив изначально является палиндромом — ответ 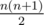 .
.
Будем обрезать с обоих концов палиндрома одинаковые символы, пока это возможно. Пусть при этом мы получили массив b длины m, его первый и последний элементы различны. Нужные нам отрезки [l, r] содержат какой-то префикс или суффикс массива b.
Найдем минимальные длины суффикса и префикса. Здесь нужно рассмотреть два случая: переходит ли кратчайший префикс/суффикс за середину массива или нет. Определить минимальные длины можно с помощью бинпоиска или проходом по массиву и поддержанием количества каждого элемента слева и справа от текущего индекса. Обозначим минимальные длины префикса за pref, и суффикса за suf. Тогда ответ 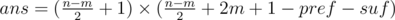 .
.
Асимптотика O(n) или  .
.
Переведем каждое число в двоичную систему счисления, для одного числа это делается MAXBITS2 c малой константой, если хранить число в системе счисления с основанием 109 или 1018. MAXBITS ≤ 2000.
Для решения задачи нам потребуется небольшая модификация алгоритма Гаусса. Будем обрабатывать запросы по одному, проделывать итерацию алгоритма Гаусса, и поддерживать следующую информацию, для бита с индексом i хранить индекс p[i] запроса, или - 1, если такого запроса нет, у которого этот бит является младшим выставленным после его(запроса) нормировки. Нормировкой я называю, процесс, в котором число приводится к такому виду, что его индекс наименьшего выставленного бита максимален. При нормировке мы можем XOR-ить число с любыми другими числами из запросов с индексами меньше текущего. Также нам понадобится информация о том, с числами из каких запросов мы проXOR-или текущее число чтобы его отнормировать, будем хранить это в битсете x[j], где j-индекс запроса.
Итак, обрабатывая очередной запрос v, мы пробегаем по его битам от младшего к старшему. В случае если текущий бит i выставлен, мы пытаемся обнулить его. Если p[i] = - 1, то обнулить этот бит нельзя и мы заканчиваем обработку этого запроса, иначе XOR-им текущее число с отнормированным числом из запроса p[i], а так же XOR-им x[v] с x[p[i]]. Если после обработки запросов нам удалось обнулить число, тогда ответ на запрос — да, и в битсете x[v] содержится множество индексов являющееся ответом, иначе — нет.
Асимптотика решения O(m × MAXBITS × (MAXBITS + m)) с малой константой, засчет битового сжатия.
Построим heavy - light декомпозицию дерева и запишем все строки соответствующие heavy-путям идущим вверх и вниз в одну строку T.
Обрабатывая очередной запрос разобьем пути (a, b) и (c, d) на части, целиком принадлежащие heavy-путям. Таких частей будет  . Заметим, что каждой части пути соответствует некоторая подстрока T.
. Заметим, что каждой части пути соответствует некоторая подстрока T.
Теперь для ответа на запрос нам необходимо находить наибольший общий префикс двух подстрок в строке. Это можно сделать, найдя суффиксный массив строки T, массив lcp и построить sparsetable на минимумы на нем.
Асимтотика: 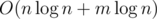
Для лучшего понимания ознакомьтесь с моим решением.
P.S. Вместо суффиксного массива можно использовать хэши, сохраняя асимптотику.
P.P.S. Решения, использующие двоичный подъем и хэши, отсекались по времени большими тестами.









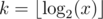 . Тогда видно, что
. Тогда видно, что 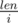 раз,
раз, 
