This editorial corresponds to 2019 Summer Petrozavodsk Camp, Day 8: XIX Open Cup Onsite, a.k.a "Jingzhe Tang Contest 2", held on Sept. 1st, 2019. Moreover, this problem set is a selection of "CCPC-Wannafly Winter Camp 2018, Day 2 (Div. 1 & Div. 2)" held on Jan 30th, 2019.
Feel free to comment on the tutorials listed in the following (with some follow-up questions left to readers). Hope you enjoy solving these problems.
The number of updates can be counted as the number of ordered pairs $$$(u, v)$$$ such that when $$$u$$$ is going to be removed, there exists at least one path between $$$u$$$ and $$$v$$$.
If the path between $$$u$$$ and $$$v$$$ is unique in the original graph, we can conclude that pair exists if $$$u$$$ is the first removed node on the path with respect to an order, and $$$\frac{1}{cnt(u, v)}$$$ of all possible orders would meet this condition, where $$$cnt(u, v)$$$ is the number of nodes on the unique path between $$$u$$$ and $$$v$$$ (inclusive).
In other cases, there exist exactly two paths between $$$u$$$ and $$$v$$$ at the beginning, each passing through one part of the only cycle in the graph. Let the number of nodes on these two paths be $$$x$$$, $$$y$$$ respectively, and the number of their common nodes be $$$z$$$. The probability that an order corresponds to this pair is $$$\frac{1}{x} + \frac{1}{y} - \frac{1}{x + y - z}$$$.
Let $$$p_1, p_2, \ldots, p_m$$$ be the nodes on the only cycle in order. Let's for each $$$p_i$$$ ($$$i = 1, 2, \ldots, m$$$) build a rooted tree from $$$p_i$$$ without passing any edges on the cycle.
We can firstly handle the case that the path between $$$u$$$ and $$$v$$$ is unique, which implies $$$u$$$ and $$$v$$$ are in the same rooted tree we have built. In this case, we only need to count the number of paths for each possible length, so we can use Centroid Decomposition with Number-Theoretic Transform to do this in total time complexity $$$\mathcal{O}(n \log^2 n)$$$.
Then we have to handle the case passing through the cycle. We can use Divide and Conquers to calculate the contribution of $$$(u, v)$$$, that is, when we merge information from $$$[L, M]$$$ and $$$[M + 1, R]$$$ into $$$[L, R]$$$, we can count for pairs $$$(u, v)$$$ such that $$$u$$$ is from the union of trees whose roots are $$$p_L, p_{L + 1}, \ldots, p_{M}$$$ and $$$v$$$ is from that for $$$p_{M + 1}, p_{M + 2}, \ldots, p_{R}$$$, and vice versa. This part can be done in time complexity $$$\mathcal{O}(n \log n \log m)$$$.
By the way, it is not difficult to count the number of paths for each possible length if the given graph is a cactus.
103652B - Linear Congruential Generator
Note that $$$X_i \bmod (X_j + 1) = X_i - \left \lfloor \frac{X_i}{X_j + 1} \right \rfloor (X_j + 1)$$$, and the number of pairs $$$\left(X_j, \left \lfloor \frac{X_i}{X_j + 1} \right \rfloor\right)$$$ is $$$\mathcal{O}\left(\sum_{i = 1}^{m}\left(\left \lfloor \frac{m - 1}{i} \right \rfloor + 1\right)\right) = \mathcal{O}(m \log m)$$$. If we can get the number of occurrences in an interval of the sequence for values in $$$[0, m)$$$ and calculate the partial sum, we can get the contribution of all $$$X_i$$$ for each pair $$$(X_j, k)$$$ such that $$$k (X_j + 1) \leq X_i < (k + 1) (X_j + 1)$$$, and solve the problem in time complexity $$$\mathcal{O}(m \log m)$$$.
Applying the pigeonhole principle, there must exist two integers $$$p$$$ and $$$q$$$ such that $$$0 \leq p < q \leq m$$$ and $$$X_p = X_q$$$. Also, for any non-negative integer $$$k$$$, we have $$$X_{p + k} = X_{q + k}$$$, and thus $$$\{X_n\}_{n = p}^{\infty}$$$ is a periodic sequence. We can easily count the number of occurrences for all possible values in $$$[l_1, r_1]$$$ and $$$[l_2, r_2]$$$ respectively in total time complexity $$$\mathcal{O}(m)$$$.
103652C - Fibonacci Strikes Back
If you are very familiar with quadratic congruences, you will know that, under the given data range, the number of candidate positions for the answer in a period of the $$$P$$$-Fibonacci sequence in modulo $$$10^k$$$ is relatively small, like $$$8$$$, and positions for $$$10^k$$$ are easy to obtain from positions for $$$10^{k - 1}$$$. Together with a series of rough analyses, you can write a Breath-First Search to find the answer.
Let's solve the problem step by step. First, we can prove that $$$\{(F_{k + 1}, F_k)\}_{k = 0}^{\infty}$$$ is a pure periodic sequence in modulo any integer $$$m$$$, as we can build an invertible matrix $$$A = \begin{bmatrix} 0 & 1 \\ 1 & P \end{bmatrix}$$$ such that $$$A^k = \begin{bmatrix} F_{k — 1} & F_k \\ F_k & F_{k + 1} \end{bmatrix}$$$.
Let $$$L(m)$$$ be the period length of the $$$P$$$-Fibonacci sequence in modulo $$$m$$$, which means $$$F_i \equiv F_{i + L(m)} \pmod{m}$$$ for any position $$$i$$$. We can try to find all possible $$$x$$$ such that $$$0 \leq x < L(10^k)$$$ and $$$F_x \equiv F_{F_n} \pmod{10^k}$$$, and then for each $$$x$$$, find all possible $$$y$$$ such that $$$0 \leq y < L(L(10^k))$$$ and $$$y \equiv F_x \pmod{L(10^k)}$$$. The answer $$$n$$$ must be in the form of $$$(y + t \cdot L(L(10^k))$$$, so we can find the smallest integer $$$t$$$ for each $$$y$$$ such that $$$n \geq m$$$, and when $$$(F_{F_n} \bmod 10^k)$$$ has leading zeros ($$$k > 1$$$), $$$F_{F_n} \geq 10^k$$$.
Before that, we have to precalculate $$$L(10^k)$$$ and $$$L(L(10^k))$$$ first. In number theory, we know that
- $$$L({p_1}^{e_1} {p_2}^{e_2} \ldots {p_t}^{e_t}) = \mathrm{lcm}(L({p_1}^{e_1}), L({p_2}^{e_2}), \ldots, L({p_t}^{e_t}))$$$, e.g. $$$L(10^k) = \mathrm{lcm}(L(2^k), L(5^k))$$$;
- $$$p^{e - 1} L(p) | L(p^e)$$$ for any prime $$$p$$$ and any positive integer $$$e$$$, e.g. $$$2^{k - 1} L(2) | L(2^k)$$$;
By enumerating different possible $$$P$$$, we can get $$$L(2) \in \{2, 3\}$$$, $$$L(5) \in \{12, 20\}$$$, so $$$\frac{L(10^k)}{10^{k - 1}} \in \{3, 6, 10, 15\}$$$ when $$$k \geq 3$$$. Together with $$$L(3) \in \{2, 8\}$$$, we have $$$\frac{L(L(10^k))}{10^{k - 2}} \in \{3, 12, 75, 100\}$$$ when $$$k \geq 5$$$. Cases for smaller $$$k$$$ are trivial, and by the way, for convenience of computing, we can calculate the $$$P$$$-Fibonacci sequence in modulo $$$3 \cdot 10^k$$$ when $$$k \geq 3$$$, which is the lowest common multiple of all possible modulo numbers.
Then, we have to prove another insight~--- for any value $$$v$$$, the number of positions $$$x$$$ such that $$$F_x \equiv v \pmod{10^k}$$$ is small. Obviously, it only depends on the number of possible values $$$F_{x - 1}$$$, as each possible pair $$$(F_{x - 1}, F_x)$$$ appears in a period only once. As we know $$$\mathrm{det}(A^x) = \mathrm{det}^x(A) = (-1)^x$$$ and $$$\mathrm{det}(A^x) = F_{x - 1} F_{x + 1} - F^2_x$$$, we can get a equation $$$F^2_{x - 1} + P F_x F_{x - 1} - F^2_{x} \equiv (-1)^x \pmod{10^k}$$$, which can be rewritten as in the form of $$$(2 u + a)^2 \equiv b \pmod{4 \cdot 10^k}$$$, when $$$F_x$$$ and the parity of $$$x$$$ are given.
The number of solutions $$$x$$$ in modulo $$$2^{k + 2} \cdot 5^k$$$ for the equation $$$x^2 \equiv y$$$ is the product of numbers of solutions in modulo $$$2^{k + 2}$$$ and $$$5^k$$$ separately, so we only care about the number of solutions in modulo a power of a prime $$$p^e$$$. Let's discuss in several cases.
- When $$$y \equiv 0 \pmod{p^e}$$$, each solution $$$x$$$ only needs to satisfy $$$p^{\left \lceil e / 2 \right \rceil} | x$$$, so the number of solutions is $$$p^{\left \lfloor e / 2 \right \rfloor}$$$;
- When $$$y = p^u \cdot v$$$, $$$1 \leq u < e$$$, $$$p \nmid v$$$, if there exists any solution, then $$$2 | u$$$ and $$$p^{u / 2} | x$$$. Assuming that the number of solutions for the equation $$${x'}^2 \equiv v \pmod{p^{e - u}}$$$ be $$$cnt$$$, the number of solutions for the equation $$$x^2 \equiv y \pmod{p^e}$$$ is $$$p^{u - u / 2} cnt$$$;
- When $$$p \nmid y$$$ and there exists a primitive root $$$g$$$ in modulo $$$p^e$$$ (i.e. $$$p$$$ is odd or $$$e \leq 2$$$), let $$$x \equiv g^u, a \equiv g^v \pmod{p^e}$$$, and then we know $$$2 u \equiv v \pmod{\varphi(p^e)}$$$, which is a linear congruence having at most $$$2$$$ solutions;
- When $$$p \nmid y$$$, $$$p = 2$$$, $$$e > 2$$$, we can use a pseudo-primitive root $$$g'$$$ to represent all values in modulo $$$p^e$$$ as in the form of $$$(-1)^u {g'}^v$$$, so it tells us the number of solutions is at most $$$4$$$.
Since $$$\gcd(P, 10^{18}) \in \{1, 2, 4\}$$$, we don't have to handle some larger cases, such as, finding $$$x$$$ with $$$F_x \equiv 1 \pmod{10^k}$$$, when $$$k = 18$$$, $$$P = 10^{k / 2}$$$, in which case the $$$P$$$-Fibonacci sequence is $$$[0, 1, P, 1, 2 P, 1, 3 P, \ldots]$$$, and the number of positions for $$$1$$$ is $$$\frac{10^k}{P} = 10^{k / 2}$$$. Therefore, based on the above rules and a few discussions, we can conclude that for any $$$k$$$, the number of solutions in $$$[0, L(10^k))$$$ for $$$F_x \equiv v \pmod{10^k}$$$ is at most $$$8$$$. (Although $$$(2 u + a)^2 \equiv b \pm 1 \pmod{4 \cdot 10^k}$$$ has $$$16$$$ solutions $$$u$$$ in modulo $$$2 \cdot 10^k$$$, every two solutions $$$u$$$ are equivalent in modulo $$$10^k$$$.) This can help us avoid any calculation about quadratic congruences. That is, we can find all solutions in modulo $$$10^e$$$ and transform them into solutions in modulo $$$10^{e + 1}$$$. More specifically, for each solution $$$x \equiv x_0 \pmod{L(10^e)}$$$ for the former case, we can examine if $$$x \equiv x_0 + t \frac{L(10^{e + 1})}{L(10^e)} \pmod{L(10^{e + 1})}$$$ is a solution for the latter case, and that works very efficiently. Note that when it comes to finding $$$y \equiv F_x \pmod{L(10^k)}$$$, the number of solutions may double.
If we just find solutions for $$$F_x \equiv F_{F_n} \pmod{10^k}$$$ and $$$y \equiv F_x \pmod{L(10^k)}$$$ forcibly, the time complexity will be $$$\mathcal{O}(8 \cdot 16 \cdot (120 + 10 k))$$$. If we prepare some information for $$$k < 3$$$, the time complexity can be even better.
Since every non-special cell has no traversable edge, we can only build an undirected graph for special cells, and the problem can be formed as calculating the cost of a minimum $$$s$$$-$$$t$$$ cut for every two nodes.
In fact, Gomory-Hu tree shows that we can build a weighted tree for these nodes such that each min-cut can be represented as the minimum value on the path between the source and the sink. If we can build the tree, we can easily get the answer by adding edges in decreasing order of weight.
To build the tree, we need to calculate $$$(|V| - 1)$$$ times min-cut. Fortunately, the degree of each node is at most $$$6$$$, which implies the cost of any min-cut is at most $$$6$$$, so we can use Dinic's algorithm to calculate min-cut forcibly, and the time complexity is $$$\mathcal{O}(6 |V| (|V| + |E|))$$$, where $$$|V| \leq 3000$$$, $$$|E| \leq 3 |V|$$$.
A well-known implementation uses `divide and conquers' to build the tree with vertex contractions, however, we can do it more easily. Here is a brief introduction to Gusfield's algorithm, which is also used in this problem's standard program:
- Label nodes from $$$0$$$ to $$$(|V| - 1)$$$, and set the parent of node $$$i$$$ ($$$i = 1, 2, \ldots, |V| - 1$$$) as $$$0$$$;
- For each node $$$i$$$ ($$$i = 1, 2, \ldots, |V| - 1$$$):
- Find a min-cut $$$(S, T)$$$ between $$$i$$$ and its parent $$$p_i$$$, where $$$i \in S$$$, $$$p_i \in T$$$;
- For each node $$$j$$$ such that $$$i < j$$$, $$$j \in S$$$, $$$p_j = p_i$$$, set $$$p_j$$$ as $$$i$$$.
Let $$$n = \sum_{i = 0}^{e}{a_i k^i}$$$, such that $$$a_0, a_1, \ldots, a_e$$$ are all integers between $$$0$$$ and $$$(k - 1)$$$ and $$$a_e > 0$$$. We can conclude when $$$f^m(n) = 1$$$, $$$m = e - 2 + \sum_{i = 0}^{e}{a_i}$$$.
Let's partition the interval $$$[l, r + 1)$$$ into many non-intersect subintervals, such that each subinterval is like $$$[a + b k^u, a + c k^u)$$$, where $$$a$$$ is a multiple of $$$k^{u + 1}$$$, and $$$b$$$, $$$c$$$ are integers between $$$0$$$ and $$$k$$$. Since $$$a + b k^u > 0$$$, there is only one possible $$$n = a + c k^u - 1$$$ with the maximum $$$m$$$ in each subinterval. Like working on the segment tree, we can find $$$\mathcal{O}(\log_k{n})$$$ subintervals, and merge their information to get the answer.
By the way, you may notice that $$$m$$$ must be from an integer $$$n$$$ whose length in the base of $$$k$$$ is either $$$e$$$ or $$$(e - 1)$$$, and then discuss $$$11$$$ possible cases.
It is easy to see the lower bound of the answer is $$$\left \lceil \frac{n}{|\Sigma|} \right \rceil$$$, and make it difficult to be passed by a brute-force solution~--- enumerate the position of $$$t_{m / 2 + 1}$$$ and run a DP to find the longest common subsequence (LCS) of two parts. However, we can speed up the process of calculating LCS by bit-level parallelism and pass the tests in time complexity $$$\mathcal{O}\left(\frac{n^3}{w}\right)$$$, where $$$w$$$ is the processor word size (which is $$$64$$$ on $$$64$$$-bit computers).
Assuming that we are finding LCS of $$$s_{1} s_{2} \cdots s_{p}$$$ and $$$s_{p + 1} s_{p + 2} \cdots s_{n}$$$, we can design a DP like $$$dp(i, j)$$$ which means the length of LCS of $$$s_{1} s_{2} \cdots s_{i}$$$ and $$$s_{p + 1} s_{p + 2} \cdots s_{p + j}$$$, and get $$$dp(i, j)$$$ from the maximum of $$$dp(i - 1, j)$$$ and $$$dp(i, j - 1)$$$ when $$$s_{i} \neq s_{p + j}$$$, or otherwise from $$$dp(i - 1, j - 1) + 1$$$.
Note that the transition makes $$$dp(i, j - 1) \leq dp(i, j) \leq dp(i, j - 1) + 1$$$, so we can define $$$f(i, j) = dp(i, j) - dp(i, j - 1)$$$ to convert the information into bits. Let's define $$$g(i, j) = [s_{i} = s_{p + j}]$$$, where $$$[x]$$$ is $$$1$$$ when $$$x$$$ is true, or otherwise $$$0$$$, and then with further discussion or observation, we can get the transition from $$$f(i - 1)$$$ to $$$f(i)$$$ :
- Let $$$x_1$$$, $$$x_2$$$, $$$x_k$$$ be the positions such that $$$1 \leq x_1 < x_2 < \ldots < x_k \leq n - p$$$ and $$$f(i - 1, x_t) = 1$$$ for $$$t = 1, 2, \ldots, k$$$, and define $$$x_0$$$, $$$x_{k + 1}$$$ as $$$0$$$, $$$(n - p + 1)$$$ respectively;
- for each $$$x_t$$$ ($$$t = 1, 2, \ldots, k + 1$$$):
- find the lowest position $$$u$$$ such that $$$x_{t - 1} < u \leq x_t$$$ and $$$g(i, u) = 1$$$, or in case there is no such $$$u$$$, define $$$u$$$ as $$$x_t$$$;
- set $$$f(i, u)$$$ as $$$1$$$, and $$$f(i, v)$$$ as $$$0$$$ for $$$v = x_{t - 1} + 1, x_{t - 1} + 2, \ldots, u - 1, u + 1, u + 2, \ldots, \min\{x_t, n - p\}$$$.
The above rule can be interpreted as that, for each interval in $$$f(i - 1)$$$ whose bits are all zeros except for the highest position, find the lowest position in $$$(f(i - 1) | g(i))$$$ that is $$$1$$$ (i.e. ON), and set the interval as all zeros except for the lowest ON position. This can be done by bitwise operations easily, for example, we can use $$$(f(i - 1) < < 1 | 1)$$$ to get the lowest position in each interval, use $$$((f(i - 1) | g(i)) - (f(i - 1) < < 1 | 1))$$$ to make the only difference on the lowest ON position in each interval, and then use other bitwise operations to get them.
Though we can retrieve a needed subsequence from $$$f$$$, you can do a slower DP at the end so that you can get the subsequence without any other thought. In addition, we don't need to calculate $$$g(i)$$$ for each position $$$i$$$ but for each character $$$s_i$$$, and that can be obtained by $$$(n - p)$$$ changes.
By the way, if you are familiar with computing all LCS of a given string $$$A$$$ and each substring of a given string $$$B$$$ in time complexity $$$\mathcal{O}(|A| |B|)$$$, you may find a better solution. This problem is known as the all-substrings longest common subsequence (ALCS) problem.
This is a typical 3D geometry problem. One thing you need to know is the volume of a spherical cap of radius $$$r$$$ and height $$$h$$$, which is
We can prove that no matter how the pivot is selected, each possible permutation for the deeper level appears with equal probability, so the expected number of inversions only depends on the level and the length of the interval.
Let $$$dp(i, j)$$$ be the expected number of inversions when $$$n = i$$$, $$$k = j$$$, and we have
We can calculate partial sums to optimize it into time complexity $$$\mathcal{O}(\max^2\{n\})$$$.
This unweighted graph is formed by $$$k$$$ non-intersect cliques and $$$m$$$ non-intersect chains, so it has many specialties. For example, we can conclude the maximum value of the shortest distance between any two cities is at most $$$(k + k - 1)$$$, as we can pass one edge to all the cities in the same district, and travel to any other city by passing through each district at most once.
If we take the hot air balloon at least once, for example, at the $$$i$$$-th district to travel from city $$$u$$$ to city $$$v$$$, we can conclude the minimum distance is $$$(f(i, u) + f(i, v) + 1)$$$, where $$$f(i, x)$$$ is the shortest distance from $$$u$$$ to any city in the $$$i$$$-th district. Consequently, the shortest distance from $$$u$$$ to $$$v$$$ is either the distance on the railway, if they are on the same railway, or $$$\min_{i = 1}^{k}\{f(i, u) + f(i, v) + 1\}$$$. Since the shortest distance is less than or equal to $$$(k + k - 1)$$$, we can ignore the former case at first, and correct the distence after calculating the latter case.
Let $$$d_u$$$ be the district city $$$u$$$ belongs to, and $$$g(i, j)$$$ be the shortest distance from any city in the $$$i$$$-th district to any city in the $$$j$$$-th district. Then, we have $$$f(i, u) \leq g(i, d_u) + 1$$$, and $$$\min_{i = 1}^{k}\{f(i, u) + f(i, v) + 1\} \leq \min_{i = 1}^{k}\{g(i, d_u) + g(i, d_v) + 3\}$$$.
Let's set a bitmask $$$mask_u$$$ for $$$u$$$ such that the $$$i$$$-th bit is $$$1$$$ when $$$f(i, u) = g(i, d_u) + 1$$$, or otherwise it is $$$0$$$. Then, for each pair of districts $$$(d_u, d_v)$$$, we can discuss the three possible cases of the shortest distance by $$$mask_u, mask_v$$$. For example, if $$$\min_{i = 1}^{k}\{f(i, u) + f(i, v) + 1\}$$$ is obtained from $$$(g(j, d_u) + g(j, d_v) + 1)$$$, then the $$$j$$$-th bit of both $$$mask_u$$$ and $$$mask_v$$$ must be zeros. After precalculating $$$cnt(i, S) = \sum_{d_u = i, mask_u \subseteq S}{1}$$$, we can count for each pair $$$(d_u, d_v)$$$ in time complexity $$$\mathcal{O}(2^k)$$$ by inclusion-exclusion principle.
We can use a breadth-first search to calculate $$$f(i, u)$$$ for each $$$i$$$ in time complexity $$$\mathcal{O}(n)$$$, and enumerate pairs $$$(u, v)$$$ such that $$$u$$$ and $$$v$$$ are on the same railway with distance less than $$$(k + k - 1)$$$ in time complexity $$$\mathcal{O}(n k)$$$, so the total time complexity is $$$\mathcal{O}(n k + k^2 2^k)$$$.
By the way, though we haven't proved it yet, it is showed that the number of different pairs $$$(d_u, mask_u)$$$ is at most $$$k \left({k - 1 \choose 2} + {k - 1 \choose 1} + {k - 1 \choose 0}\right)$$$, and thus it yields a solution in time complexity $$$\mathcal{O}(n k + k^6)$$$.
We call the substring $$$s_{i} s_{i + 1} \cdots s_{j}$$$ a run, denoted by $$$(i, j, d)$$$, if there exists a smallest $$$d$$$ such that
- $$$2 d \leq j - i + 1$$$;
- $$$s_{k} = s_{k + d}$$$ for $$$k = i, i + 1, \ldots, j - d$$$;
- $$$s_{i - 1} \neq s_{i + d - 1}$$$ if $$$s_{i - 1}$$$ exists;
- $$$s_{j + 1} \neq s_{j - d + 1}$$$ if $$$s_{j + 1}$$$ exists.
With respect to a strict total order $$$<$$$ on the alphabet $$$\Sigma$$$, we call a string $$$w$$$ Lyndon word if $$$w < u$$$ is true for each proper suffix $$$u$$$ of $$$w$$$. Since for a run $$$(i, j, d)$$$ we have $$$s_{j + 1} \neq s_{j - d + 1}$$$, we can always find a Lyndon word $$$s_{u} s_{u + 1} \cdots s_{v}$$$ with respect to a strict total order $$$<$$$ or its reversed order, such that $$$v - u + 1 = d$$$ and $$$i < u \leq i + d$$$. Also, it can be proved that different runs don't share any such words, and thus the number of runs is $$$\mathcal{O}(n)$$$.
By further proof, we can get $$$\sum_{(i, j, d)\text{ is a run}}{\frac{j - i + 1}{d}} \leq 3 n - 3$$$, which implies that, if we pick up all the squres as square-triples $$$(L, R, k)$$$ such that each length-$$$k$$$ substring of $$$s_{L} s_{L + 1} \cdots s_{R}$$$ is a square, the number of these square-triples are less than $$$\frac{3}{2} n$$$. If we can pick up these square-triples, we can solve the problem using some data structures.
First, let's talk about how to get these triples. There are many ways to detect runs, and then you can pick up all the square-triples. For example, you can enumerate $$$d$$$ and positions $$$1, d + 1, 2 d + 1, \ldots$$$ in the string so that you can check if two consecutive positions are in the same run and then detect the run. Alternatively, you can linearly build the Lyndon tree of the string and meanwhile get runs. The former detects all runs in time complexity $$$\mathcal{O}(n \log n)$$$, and the latter in $$$\mathcal{O}(n)$$$, in which building the suffix array of the string in linear time is required.
Then, let's see if we can maintain some data structure to solve the problem in time complexity $$$\mathcal{O}((n + q) \log n)$$$. Let's consider the relationship between a query $$$(l_i, r_i)$$$ and a square-triple $$$(L, R, k)$$$. Obviously, if the triple has any contribution to the query, it must have $$$k \leq r_i - l_i + 1$$$. Furthermore, we can split one triple $$$(L, R, k)$$$ into two triples without upper bounds, $$$(L, \infty, k)$$$ and $$$(R - k + 2, \infty, k)$$$, so that we can handle things easily. That is, for a new triple $$$(u, \infty, k)$$$, its contribution (without regard to its sign) to the query $$$(l_i, r_i)$$$ is $$$(\max\{r_i - u - k + 2, 0\} - \max\{l_i - u, 0\})$$$, which can be calculated by maintaining two Fenwick trees and enumerating intervals in increasing order of length.
The number of ways to partition a set of size $$$12$$$ into $$$4$$$ sets of size $$$3$$$ without regard to order is $$$\frac{12!}{3!3!3!3!4!} = 15400$$$. We can find these partitions through a depth-first search, and the problem can be done. By the way, we can sort sticks in increasing order of length so that we can use $$$a < b < c$$$ and $$$a + b > c$$$ to check the existence of a triangle with side lengths $$$a, b, c$$$.
One brute-force way is to enumerate three of $$$\frac{12!}{3!9!}$$$ ($$$= 220$$$) possible sets and prune when it is necessary, however, it can hardly pass all the tests.
The key insight is that, for every three equidistant vertices, we can find the only upright equilateral triangle such that these three vertices are on the triangle's sides. (We can do so for the only inverted equilateral triangle.) Based on this fact, many solutions can be designed.
For example, you can use some data structure to maintain some information for $$$l$$$ when $$$r$$$ is fixed and shifted from low to high, or even you can use Mo's algorithm to solve the problem in time complexity $$$\mathcal{O}(\max\{r\} \sqrt{T})$$$.
If you are very good at math, you can find out the combinatorial form of the answer (a polynomial of degree $$$4$$$), and then solve the problem with or without interpolation.









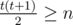 .
.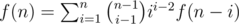 . Speed it up by divide and conquer (or Newton iteration).
. Speed it up by divide and conquer (or Newton iteration).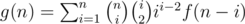 by enumerating contributions of each component.
by enumerating contributions of each component.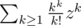 .
.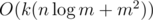 , while maintaining some statistics obtained from 2-dimensional partial sum and solving equations for each square can do this in
, while maintaining some statistics obtained from 2-dimensional partial sum and solving equations for each square can do this in 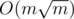 .
.
