Hi everyone.
This is my template for debugging in C++. I was inspired by Tourist's source code and modified it to my style. Here is it:
To debug, just type: debug(x, y, z...). It requires C++ 11 or above.
It can work with:
Primitive data types:
bool,int,long long,float, ...std::pair,std::string- Collection types:
std::vector,std::map,std::set, ... - Expressions
It also support multiple arguments.
How to use
Primitive data types:
bool a = true;
debug(a);
int b = 1;
float c = 2.5;
long long d = LLONG_MAX;
char e = 'e';
debug(a, b, c, d, e);
Output:
'[a] = [true]'
'[a, b, c, d, e] = [true, 1, 2.5, 9223372036854775807, 'e']'
std::pair and std::string:
pair<int, int> a = {1, 2};
pair<string, bool> b = {"abcd", false};
pair<char, float> c = {'x', 0.5};
string d = "This is a string";
pair<int, pair<int, int> > e = {1, {2, 3}};
debug(a, b, c, d, e);
Output:
'[a, b, c, d, e] = [{1, 2}, {"abcd", false}, {'x', 0.5}, "This is a string", {1, {2, 3}}]'
Note: You should only debug a pair of simple data types. For example, the debug won't work if one of pair's elements is collection type (std::vector, std::map, std::set...).
Collection types:
Basically, the debug works with collections types which you can iterate by for (auto i: a). So the debugger won't work with collection types like std::queue or std::stack.
vector<int> a = {1, 2, 3, 4};
set<int> b = {1, 2, 2, 3, 3, 4, 4, 5};
map<string, int> c;
c["string 1"] = 1;
c["string 2"] = 2;
debug(a, b, c);
unordered_map<string, int> d;
d["string 3"] = 3;
d["string 4"] = 4;
multiset<int> e = {5, 5, 4, 3, 1, 1, 2};
vector<vector<int> > f = {{1, 2, 3}};
debug(d, e, f);
Output:
'[a, b, c] = [{1, 2, 3, 4}, {1, 2, 3, 4, 5}, {{"string 1", 1}, {"string 2", 2}}]'
'[d, e, f] = [{{"string 4", 4}, {"string 3", 3}}, {1, 1, 2, 3, 4, 5, 5}, {{1, 2, 3}}]'
Note: I haven't tried the debug with other complex data types nested in collection types.
Expressions:
int a = 1;
int b = 2;
debug(a + b, a * b, a / b, a - b, a / (float)b, 2019, 2019 - 1);
Output:
'[a + b, a * b, a / b, a - b, a / (float)b, 2019, 2019 - 1] = [3, 2, 0, -1, 0.5, 2019, 2018]'
You can use the template and change it's style to what you want. Hope it would help you debug in C++ easier.









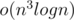 solution, which we do binary seaching for
solution, which we do binary seaching for 
