CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
43:06:32
Зарегистрироваться »
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Щедрый Кефа — Adiv2
(Авторы: Mediocrity, totsamyzed)
Рассмотрим каждый цвет по отдельности. Мы можем раздать все шарики цвета c друзьям Кефы только если c ≤ k. Потому что иначе, по принципу Дирихле, хотя бы один из друзей получит два или более шариков одинакого цвета.
Поэтому сделать нужно следующее: посчитать количество шариков каждого цвета, cntc.
А потом просто проверить, что cntc ≤ k для всех возможных c.
Сложность: O(N + K)
Находка — Bdiv2
(Автор: Mediocrity)
Первый игрок выигрывает, если в массиве есть хотя бы одно нечетное число. Давайте докажем это.
Обозначим суммарное количество нечетных чисел как T.
Тогда есть два случая:
1) T нечетное. Первый игрок может забрать весь массив и выиграть.
2) T четное. Предположим, что позиция самого правого нечетного числа pos. Тогда стратегия первого игрока такая: в первый свой ход, взять подотрезок [1;pos - 1]. Оставшийся суффикс будет иметь ровно одно нечетное число и второй игрок не сможет включить его в свой подотрезок. Поэтому, независимо от его хода, своим следующим ходом первый игрок заберет оставшиеся числа и выиграет.
Сложность: O(N)
Леха и функция — Adiv1
(Автор: Mediocrity)
Прежде всего, давайте поймем, чему равно значение F(N, K).
Для любого подмножества размера K, скажем, a1, a2...aK, мы можем уникальным образом сопоставить его с последовательностью d1, d2...dK + 1 так, что d1 = a1, d1 + d2 = a2, ..., 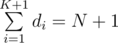 .
.
Нас интересует значение E[d1], матожидание d1. Зная основные факты о матожидании, мы можем получить следующее:
E[d1 + ... + dK + 1] = N + 1
E[d1] + ... + E[dK + 1] = (K + 1)·E[d1]
Отсюда немедленно следует, что 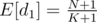 .
.
Теперь, значение 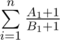 максимизурется, когда A возрастает, B убывает. Это можно доказать при помощи транснеравенства.
максимизурется, когда A возрастает, B убывает. Это можно доказать при помощи транснеравенства.
Сложность: O(NlogN)
Леха и другая игра про графы — Bdiv1
(Авторы: 244mhq, totsamyzed)
Авторское решение опирается на тот факт, что граф связен.
Мы докажем, что искомое подмножество существует если и только если все - 1 можно заменить на 0 / 1 так, что 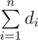 четно. Если так сделать нельзя, то решения не существует (в каждом графе сумма степеней всегда четное число). Теперь мы покажем, как построить ответ для любого теста, где можно получить четную сумму.
четно. Если так сделать нельзя, то решения не существует (в каждом графе сумма степеней всегда четное число). Теперь мы покажем, как построить ответ для любого теста, где можно получить четную сумму.
Для начала, поменяем все - 1 нужным образом.
Найдем любое остовное дерево и подвесим за любую вершину. Теперь задача стала гораздо легче.
Будем обрабатывать вершины одну за одной, в порядке глубины: от листьев к корню. Пусть текущая обрабатываемая вершина cur.
Есть два случая:
1) dcur = 0
В этом случае мы игнорируем ребро от cur до parentcur и забываем про вершину cur. Сумма степеней остается четной.
2) dcur = 1
В этом случае мы добавляем ребро от cur до parentcur в ответ, меняем значение dparentcur на противоположное и забываем про вершину cur. Как можно заменить, сумма меняет четность, когда мы меняем dparentcur, но потом снова становится четной, когда мы исключаем вершину cur. Поэтому в итоге сумма остается четной как и в первом случае.
Такими несложными манипуляциями мы получаем одно из возможных решений.
Сложность: O(N + M)
На скамейке — Cdiv1
(Авторы: Mediocrity, totsamyzed)
Разделим все числа на группы. Будем обрабатывать числа в порядке от 1 до N. Предположим, текущая позиция i. Если groupi еще не посчитано, i формирует новую группу. Присвоим уникальное число groupi. Потом для всех j таких, что j > i и a[j]·a[i] — квадрат, сделаем groupj равным groupi. Теперь произведение пары чисел дает квадрат если и только если они находятся в одной группе.
Можно использовать динамическое программирование для подсчета ответа.
F(i, j) будет обозначить количество способов расположить числа из первых i групп, образовав j плохих пар соседей.
Опишем переход из F(i, j). Обозначим размер следующей группы как size, а суммарное количество чисел, расставленных ранее, как total.
Переберем значения S от 1 до min(size, total + 1) и D от 0 до min(j, S).
S — количество кусков, на которое мы разобьем следующую группу, а D — количество существующих на данный момент плохих пар, которые мы разобьем.
Теперь добавим T к F(i + 1, j - D + size - S) (D пар разбито, size - S новых пар образовано после расположения чисел новой группы).
T — количество способов расположить числа новой группы согласно значениям S и D.
На самом деле, T есть 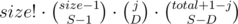 . Почему? Потому что есть
. Почему? Потому что есть 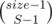 способов разбить группу размера size на S кусков.
способов разбить группу размера size на S кусков.
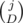 способов выбрать D из j плохих пар, которые мы разобьем. И
способов выбрать D из j плохих пар, которые мы разобьем. И 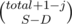 способов выбрать расположения для S - D кусков (остальные D разбивают пары, так что их позиции определены).
способов выбрать расположения для S - D кусков (остальные D разбивают пары, так что их позиции определены).
После всех подсчетов, ответ находится в F(g, 0), где g — общее количество групп.
Сложность: O(N^3)
Судьба — Ddiv1
(Авторы: Mediocrity, totsamyzed)
Используем метод разделяй и властвуй.
Допустим, текущий запрос на отрезке [L;R]. Разделим массив на две части: [1;mid] и [mid + 1;N], где 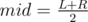 . Если наш запрос целиком принадлежит левой или правой половине, перейдем туда и повторим процесс. Иначе L ≤ mid ≤ R. Мы утверждаем, что если сформировать множества из K самых часто встречаемых чисел в левой и правой половине, ответ либо будет в этом множестве либо его нет.
. Если наш запрос целиком принадлежит левой или правой половине, перейдем туда и повторим процесс. Иначе L ≤ mid ≤ R. Мы утверждаем, что если сформировать множества из K самых часто встречаемых чисел в левой и правой половине, ответ либо будет в этом множестве либо его нет.
K самых часто встречаемых чисел можно предпосчитать. Запустим рекурсивную функцию build(node, L, R). Как при построении дерева отрезков, сначала зайдем в левого и правого сына node. Потом мы должны посчитать K самых часто встречаемых чисел для всех таких отрезков [L1;R1], что L ≤ L1 ≤ R1 ≤ R и хотя бы одно из L1 и R1 равно 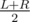 .
.
Рассмотрим все отрезки с левым концом в mid в следующем порядке: [mid;mid], [mid;mid + 1], ...[mid;R]. Если у нас уже были посчитаны K самых часто встречаемых и их количества для отрезка [mid;i], то же самое легко пересчитать для [mid;i + 1]. Мы обновляем счетчик для ai + 1 и смотрим, нужно ли что-то менять для нового списка.
То же самое делаем для отрезков с правой границей в mid. Обрабатываем в порядке [mid;mid], [mid - 1;mid], ..., [L;mid].
Теперь, заранее посчитав все это, мы можем запустить разделяй и властвуй и получить кандидатов на ответ в отрезке [L;R]. Чтобы проверить кандидата, мы можем заранее сохранить все вхождения каждого числа и потом использовать бинарный поиск для ответов на вопросы вида «Сколько раз x встречается на отрезке от L до R?»
Сложность: O(KNlogN)
В ловушке — Ediv1
(Автор: Mediocrity)
Путь от u до v можно разбить на блоки размером 256 вершин и (возможно) последний блок с меньшим количеством вершин. Этот последний блок рассмотрим отдельно, пройдя все его вершины в лоб. <br. Теперь нужно рассмотреть блоки длины 256. Каждый из них задается двумя числами: x — последняя вершина блока, d — 8 старших битов. Мы можем предпосчитать эти значения и использовать их для ответов на запросы.
Поговорим о предпосчете answer(x, d). Зафиксируем x и 255 вершин после x. Легко заметить, что младшие 8 битов всегда будут такими: 0, 1, ..., 255. Нужно закинуть в бор все значения 0 xor ax, 1 xor anextx и т.д.
Теперь, нужно перебрать все значения d от 0 до 255 и единственное, что остается сделать — найти в боре число, xor которого с 255·d дает максимальный результат.
Сложность: O(NsqrtNlogN)
Hi all,
Recently I had a talk with ko_osaga and he told me that unfortunately he can't use #include <bits/stdc++.h> because his operating system is OS X. I was surprised to know that because I'm using this header on OS X without any troubles.
When I explained him how I manage to do that he told me I should compose a topic about this because it will help many people :)
So I will try to cover two things in my post:
a) How to compile #include <bits/stdc++.h> in Sublime text?
b) How to compile C++11 features like lambdas, auto, etc. in Sublime text?
Let's get started.
#include<bits/stdc++.h> usage
3 easy steps.
1) Install Xcode
2) Download stdc++.h from my GitHub. The file is not mine of course, I just googled it and commented out including cstdalign library because it just wouldn't compile on my mac (I wasn't interested enough to figure out why).
3) Now you must simply put stdc++.h into /Applications/Xcode.app/Contents/Developer/Platforms/ChosenTargetPlatform/Developer/SDKs/ChosenMacOSSDK/usr/include/bits
Done!
C++11 features usage
Here you will need a custom build system for Sublime text. It's easy to create!
3 easy steps again.
1) Download gpp.sublime-build from my GitHub.
2) Go to Sublime, then select Tools->Build System->New Build System. This is the place where you should paste gpp.sublime-build. Don't forget to save the file.
3) Relaunch Sublime, from now on your new build system will be available at Tools->Build System.
Done!
I hope someone will find this helpful. Thanks for your attention! :)
| Название |
|---|