Introduction
I was fiddling around with the codeforces API and came up with the following average difficulty calculations for Div 2 only contest problems in 2021.
- A: 826
- B: 1122
- C: 1544
- D: 2000
- E: 2373
- F: 2736
Caveats
The data is a little messy. I ignored problems like D1, D2 etc. Also the code can't seem to find the shared problems in Div 2 when there is a Div 1 contest occurring at the same time.









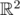 where it has the maximum
where it has the maximum 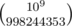 mod
mod  is a pain because of fractions. If you try to avoid them by multiplication by denominators things overflow pretty quickly.
is a pain because of fractions. If you try to avoid them by multiplication by denominators things overflow pretty quickly. 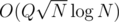 and exceeding the time limit. In general if you are given an interval of length
and exceeding the time limit. In general if you are given an interval of length 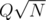 do you want in order to be confident that a square root decomposition will pass the time constraint? Also are there standard limits used in Codeforces deliberately set to prevent square root decomposition based approaches?
do you want in order to be confident that a square root decomposition will pass the time constraint? Also are there standard limits used in Codeforces deliberately set to prevent square root decomposition based approaches? 
