Problem statement :

There are N planets in the galaxy. For each planet i, it has two possible states : empty, or it is connected to some other planet j ≠ i with a one-way path. Initially, each planet is in the empty state (i.e. there are no paths between any pair of planets)

There are three types of operations :

1. If planet i is in empty state, connect it with planet j with a one-way path (i and j are distinct)

2. If planet i is currently connected to planet j with a one-way path, remove that path. Consequently, planet i is now in empty state again

3. For a pair of planets u, v, find a planet x such that one can travel from u to x and v to x. If there are multiple such planets, find the one where the total distance travelled by u and v is minimized (distance is the number of paths it passes through). If there are no solutions, output  - 1.

Q, N ≤ 10⁶. Time limit is 10 seconds.

One of the official solutions uses splay tree to solve this problem, but I have no idea how it works (I haven't use splay trees before). Can anyone tell me how to use splay tree on this problem? Thanks.

Recently I encountered a problem which is very similar to RMQ.

Abridged Statement : First, you have an empty array. You have two operations :

1. Insert a value v between positions x - 1 and x (1 ≤ x ≤ k + 1) where k is the current size of the array.(positions are 1-indexed)

2. Find the maximum in the range [l, r] (i.e. the maximum from the positions l to r inclusive)

There are at most Q ≤ 250000 queries.

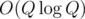My current solution uses SQRT decomposition but it was not fast enough to get AC. I was wondering if there is an or 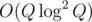solution.

Edit : Forgot to mention that the queries must be answered online (it's actually function call), so offline solutions doesn't work.

Problem Statement

Abridged Problem Statement : Given a₁, a₂, ..., a_n, find the number of permutations of these numbers such that |a₁ - a₂| + |a₂ - a₃| + ... + |a_n - 1 - a_n| ≤ L where L is a given integer.

The editorial given is quite brief and the sample code is nearly unreadable. I have no idea how to do the dp.

Can anyone explain the solution? Thanks.

UPD : Thanks to ffao for the hint! I finally got how the dp works. The unobfuscated code with comments is here.

Reminder that Google Distributed Code Jam Online Round 1 starts at this time.

Good luck to all people participating!

I was trying to solve this problem.

I could only figure out the naive solution. (DFS from each vertex) I think I have encountered similar problems before but I couldn't solve them either. How do I solve this kind of problem?

I keep getting this message when I try to package the problem in polygon :

PackageException: There exists a test where checker crashes.

Why does this error show up?

(I'm using the standard checker that compares sequences of integers)

Reminder that Ad Infinitum 15 — Math Programming Contest starts at Apr 15 2016, 11:30 pm CST.

T-shirts for top 10 ranks on leaderboard.

1. COLOR

This problem is trivial. Note that we want the resulting string to be monochromatic and thus we can just choose the color with maximal occurences and change the remaining letters into the color.

2. CHBLLNS

This problem is also trivial. For each color, we take k - 1 balls, or if there're less than k - 1 balls, take all the balls. Currently, there are at most k - 1 balls for each color. Then, take one more ball. By pigeonhole principle, there exists k balls of same color. So, this is our answer.

3. CHEFPATH

This problem is not hard. WLOG, assume n ≤ m. If n = 1, then the task is possible if and only if m = 2 for obvious reasons. Otherwise, if m, n are both odd, then coloring the board in a checkerboard fashion can show that no such path exist. If one of m, n is even, then such path exists. (it's not hard to construct such path)

4. BIPIN3

In fact, the answer is the same for any tree. For the root vertex we can select k possible colors. For each children, note that we can select any color except the color of the parent vertex, so there're k - 1 choices. So, in total there are k·(n - 1)^k - 1 possible colorings. To evaluate this value, we use modular exponentiation.

5. FIBQ

The idea of this problem is to convert the sum in matrix language. Let T be the matrix[\begin{bmatrix} 1 & 1 \ 1 & 0 \end{bmatrix} ]

Additionally, let I be the identity matrix. Then, our desired answer will be the top right element of (T^a_l + I)(T^a_l + 1 + I)...(T^a_r + I). Now, to support the update queries, just use a segment tree. The segment tree from this link is perfect for the job.

6. DEVGOSTR

Despite it's appearance, this problem is actually very simple. For A = 1, there is at most 1 possible string, namely the string consisting of all `a's. The background of this problem is Van der Waerden's Theorem. According to the Wikipedia page, the maximal length of a good string for A = 2 is 8 and the maximal length for a good string for A = 3 is 26. Now, for A = 2 we can brute force all possible strings. However, for A = 3 we need to brute force more cleverly. The key is to note that if a string s is not good then appending any letter to s will not make it good. So, we just need to attempt to append letters to good strings. This pruning will easily AC the problem.

7. AMAEXPER

Call a point that minimizes the answer for a subtree rooted at r the king of r. If there are mutiple kings choose the one closer to r. The problem revolves around an important lemma :

Lemma : For the subtree rooted at r, consider all children of r. Let l be the children such that the distance from r to the furthest node in the subtree rooted at l is the longest. If there are multiple l, then r is the king. Otherwise, either r is the king of the node in the subtree rooted at l is the king.

Sketch of proof : Suppose not, then the maximal distance from some other vertex will be the distance from that node to root + the distance from root to the furthest node in the subtree rooted at l, so choosing r is more optimal.

Thus, for we can actually divide the tree into chains. A chain starts from some vertex v and we keep going down to the children l. For each node r, we store the distance to root, the maximal distance from r to any vertex in its subtree, as well as the maximal distance IF we don't go down to children l. (this distance is 0 if r has only 1 children) Now, for each chain, we start from the bottom. We also maintain a king counter starting from the bottom. At first, the answer for the bottom node is the maximal distance stored for that node. Then, as we go up to the top of the chain, note that the possible places for the king is on the chain and will not go below the king for the node below. Thus, we can update the king counter in a sliding window like fashion. How do we find the answer for each node? This value can be calculated in terms of the numbers stored on each node, and using an RMQ we can find the desired answer. The details for this will not be included here.

8. FURGRAPH

The key observation for this problem is the following : Instead of weighing the edges, for each edge with weight w, we increase w to the endpoints of the edge (note that for self-loops the vertex will be added twice). Then, the difference of score of Mario and Luigi is just the difference of the sum of weights on the vertices they have chosen, divided by 2. Why? If an edge has its endpoints picked by Mario (or Luigi), then Mario (or Luigi)'s score will increase by 2w. If each person pick one of the endpoints, then the difference of score is unchanged, as desired. Now, Mario and Luigi's strategy is obvious : They will choose the vertex with maximal possible weight at the time, so letting a₁ ≤ a₂ ≤ ... ≤ a_n be the weights of the vertices in sorted order, the answer is a_n - a_n - 1 + a_n - 2... + ( - 1)^n - 1a₁, i.e. the alternating sum of weights in sorted order.

Using this observation alone can easily give us Subtask 2. We can naively store the vertex weights in a map and update as neccesary. For each query, just loop through the map and calculate the alternating sum.

Subtask 3 requires more optimization. We will use sqrt-decomposition with an order statistic tree to store the vertex weights in sorted order. Note that for each update, we're cyclicly shifting the values of a_l to a_r, for some l, r which can be found from our order statistic tree. Then, we update a_r as a_l + w. To efficiently perform these queries, we divide the array (of vertex weights) into parts of elements each. We start from element l. For each block we store a deque containing the elements, the sum of elements (we store the elements as negative if we want to subtract the value when calculating the alternating sum for convenience), and the sign of the elements in the block. We iterate through the elements and perform the neccesary updates until we reach the end of block. Then, for updating entire blocks, we perform the neccesary updates on the values, negate the sign, and since we're using deque we can pop front and push back the desired element (namely the next element). Then, when we reach the block containing r, we iterate naively again. The total complexity is . 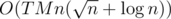My solution with this algorithm ACs the problem.

9. CHNBGMT

Unfortunately, I only get the first 3 subtasks to this problem.

This problem is similar to this, except it's harder. The solution for that problem uses Lindstrom-Gessel-Viennot Lemma. We can apply that lemma to this problem as well.

You can see how to apply the lemma from the old CF problem. Now, the problem reduces to finding the number of ways to go from a_i to b_j for 1 ≤ i, j ≤ 2, and finding the determinant of the resulting 2 by 2 matrix.

For subtasks 1 and 2, M and N are small so we can find these values using a simple dp. In particular, we can use something like dp[i][j][k] =  number of ways to get to (i, j) passing through exactly k carrots. Since M, N ≤ 60, this solution can easily pass.

For subtask 3, N, M ≤ 10⁵. However, we are given that C = 0. For N = 2 or M = 2 the answer can be calculated manually. So, from now onwards, we assume M, N ≥ 3. Then finding the values is equivalent to computing binomial coefficients. (The details are trivial). So, all it remains is to know how to compute binomial coefficients mod MOD where MOD ≤ 10⁹ is not guaranteed to be a prime.

Firstly, the obvious step is to factor MOD into its prime factors. Thus, we can compute the answer mod all the prime powers that are factors of MOD and combine the results with Chinese Remainder Theorem. How do we find the result mod p^k? This is trivial. We just need to store v_p(n) of the numbers and the remainder of the number mod p^k when we divide out all factors of p. Now, compute modular inverse mod p^k assuming that the value is not divisible by p can be done using Euler's Theorem the same way we find modular inverse mod p.

I would like to know how to get the other subtasks where C > 0.

For this problem, the tutorial states that maintaining the sum of a Geometric Progression is a simple problem that can be solved using Segment Tree. However, I don't know how to do this (I think Lazy Propogation should be involved). Any help please?

I have ideas on problems and would like to write a codeforces round, so how should I do so? (I know some basics for writing problems (though I'm not quite familiar with the testlib library).)

UPD : I finished all problems and uploaded all of them on polygon, but I still haven't get a reply (my message wasn't even seen yet) :(

UPD2 : Got a reply. Thanks to everyone who commented!

Abridged Problem Statement : You have a list of N distinct words, and you want to print K of them. You have a very basic text editor : It supports 3 types of operations: typing a letter, deleting the previous letter, and printing the current document. You need to leave the document empty after printing K words. What's the minimum number of operations required to get the job done?

Constraints : 1 ≤ K ≤ N ≤ 300 The total length of all N words in each set will be at most 100, 000 characters.

Solution :

Name the words s₁, s₂, ..., s_N. Let s₀ = "". We initially have s₀ on the document. After some operations, we want to print k of s₁, s₂, ..., s_N and change the document to s₀. For some pair of string s_i, s_j, how many operations do we need to print s_j if we have a document with s_i? Let p be the length of the Longest Common Prefix of s_i and s_j. We can compute this naively in O(min(|s_i|, |s_j|)). Then, we need to delete |s_i| - p characters, type |s_j| - p characters, and print it (1 operation), for a total of |s_i| + |s_j| - 2p + 1 operations. We can precalculate this value for each pair of words s_i, s_j in a short time.

Now, suppose we have chosen our K words s₁, s₂, ..., s_K. In which order do we print them in order to use a minimum amount of operations? We claim that in fact, if we print the strings in lexicographical order, we will use the minimum amount of operations. Suppose not, let s₁, s₂, ..., s_K be arranged in lexicographical order. Suppose we print the words in the sequence s₁, s₂, ..., s_i - 1, s_j, s_i + 1, ..., s_j - 1, s_i, s_j + 1, ..., s_K, with i < j. Let a₁, a₂, ..., _K be the length of word s₁, s₂, ..., s_K respectively and denote the length of the Longest Common Prefix of s_a and s_b by L(a, b). Note that L(i, j) ≥ L(i, k) if i < j < k. Suppose to the contrary the longest common prefix of s_i and s_k have longer length than the longest common prefix of s_i and s_j. Then, let p be the longest common prefix of s_i and s_k. The prefix of s_j does not contain p but this contradicts the fact that s_i, s_j, s_k are increasing in lexicographical order. Thus, the inequality holds. We'll use this inequality many times in the calculations below. It can be easily seen that the total number of operations used is 2(a₁ + a₂ + ... + a_K) - 2(L(1, 2) + L(2, 3) + ... + L(i - 1, j) + L(j, i + 1) + ... + L(j - 1, i) + L(i, j + 1) + ... + L(K - 1, K)). Compare this to when the words are printed in lexicographical order. Firstly, if j > i + 1, we just need to compare L(i - 1, j) + L(j, i + 1) + L(j - 1, i) + L(i, j + 1) and L(i - 1, i) + L(i, i + 1) + L(j - 1, j) + L(j, j + 1). We want the former to be at most the latter. Indeed, L(i - 1, i) ≥ L(i - 1, j), L(i, i + 1) ≥ L(i, j - 1), L(j - 1, j) ≥ L(i + 1, j), L(j, j + 1) ≥ L(i, j + 1), since the words are arranged in lexicographical order. So, summing up yields the desired inequality. Now suppose j = i + 1. We want to compare L(i - 1, i + 1) + L(i + 1, i) + L(i, i + 2) and L(i - 1, i) + L(i, i + 1) + L(i + 1, i + 2). Again, we have L(i - 1, i) ≥ L(i - 1, i + 1), L(i + 1, i + 2) ≥ L(i, i + 2), as desired. So, printing the words lexicographically is the optimal way.

Now, we already have our cruical step. It remains to select the K words that minimize the amount of operations. We can do this by dynamic programming. First sort the N words in lexicographical order. Let dp[end][parts] be the minimum number of operations needed to print parts number of words all of whose index is at most end and the last word printed has index end. We want min(dp[1][k], dp[2][k], ..., dp[n][k]). If end < parts, we let dp[end][parts] be INF.

Let cost(i, j) be the number of operations needed to print word j if our current document is word i. Recall that we already know how to compute cost(i, j) in O(1) since we already precomputed the values.

Now, how do we find dp[end][parts]? It is the minimum of dp[i][parts - 1] + cost(i, end) among 1 ≤ i ≤ end - 1. Time complexity is O(n^2k). Finally, don't forget to add the cost from s₀ to s_i. (in the beginning and end).

6235741

/** Micro Mezzo Macro Flation -- Overheated Economy ., Last Update: Feb. 12th 2013 **/ //{

/** Header .. **/ //{
#define LOCAL
#include <functional>
#include <algorithm>
#include <iostream>
#include <fstream>
#include <sstream>
#include <iomanip>
#include <numeric>
#include <cstring>
#include <cassert>
#include <cstdio>
#include <string>
#include <vector>
#include <bitset>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <list>
#include <set>
#include <map>

using namespace std;

#define REP(i, n) for (int i=0;i<int(n);++i)
#define FOR(i, a, b) for (int i=int(a);i<int(b);++i)
#define DWN(i, b, a) for (int i=int(b-1);i>=int(a);--i)
#define REP_1(i, n) for (int i=1;i<=int(n);++i)
#define FOR_1(i, a, b) for (int i=int(a);i<=int(b);++i)
#define DWN_1(i, b, a) for (int i=int(b);i>=int(a);--i)
#define REP_C(i, n) for (int n____=int(n),i=0;i<n____;++i)
#define FOR_C(i, a, b) for (int b____=int(b),i=a;i<b____;++i)
#define DWN_C(i, b, a) for (int a____=int(a),i=b-1;i>=a____;--i)
#define REP_N(i, n) for (i=0;i<int(n);++i)
#define FOR_N(i, a, b) for (i=int(a);i<int(b);++i)
#define DWN_N(i, b, a) for (i=int(b-1);i>=int(a);--i)
#define REP_1_C(i, n) for (int n____=int(n),i=1;i<=n____;++i)
#define FOR_1_C(i, a, b) for (int b____=int(b),i=a;i<=b____;++i)
#define DWN_1_C(i, b, a) for (int a____=int(a),i=b;i>=a____;--i)
#define REP_1_N(i, n) for (i=1;i<=int(n);++i)
#define FOR_1_N(i, a, b) for (i=int(a);i<=int(b);++i)
#define DWN_1_N(i, b, a) for (i=int(b);i>=int(a);--i)
#define REP_C_N(i, n) for (int n____=(i=0,int(n));i<n____;++i)
#define FOR_C_N(i, a, b) for (int b____=(i=0,int(b);i<b____;++i)
#define DWN_C_N(i, b, a) for (int a____=(i=b-1,int(a));i>=a____;--i)
#define REP_1_C_N(i, n) for (int n____=(i=1,int(n));i<=n____;++i)
#define FOR_1_C_N(i, a, b) for (int b____=(i=1,int(b);i<=b____;++i)
#define DWN_1_C_N(i, b, a) for (int a____=(i=b,int(a));i>=a____;--i)

#define ECH(it, A) for (__typeof(A.begin()) it=A.begin(); it != A.end(); ++it)
#define REP_S(i, str) for (char*i=str;*i;++i)
#define REP_L(i, hd, nxt) for (int i=hd;i;i=nxt[i])
#define REP_G(i, u) REP_L(i,hd[u],suc)
#define DO(n) for ( int ____n ## __line__ = n; ____n ## __line__ -- ; )
#define REP_2(i, j, n, m) REP(i, n) REP(j, m)
#define REP_2_1(i, j, n, m) REP_1(i, n) REP_1(j, m)
#define REP_3(i, j, k, n, m, l) REP(i, n) REP(j, m) REP(k, l)
#define REP_3_1(i, j, k, n, m, l) REP_1(i, n) REP_1(j, m) REP_1(k, l)
#define REP_4(i, j, k, ii, n, m, l, nn) REP(i, n) REP(j, m) REP(k, l) REP(ii, nn)
#define REP_4_1(i, j, k, ii, n, m, l, nn) REP_1(i, n) REP_1(j, m) REP_1(k, l) REP_1(ii, nn)

#define ALL(A) A.begin(), A.end()
#define LLA(A) A.rbegin(), A.rend()
#define CPY(A, B) memcpy(A, B, sizeof(A))
#define INS(A, P, B) A.insert(A.begin() + P, B)
#define ERS(A, P) A.erase(A.begin() + P)
#define BSC(A, x) (lower_bound(ALL(A), x) - A.begin())
#define CTN(T, x) (T.find(x) != T.end())
#define SZ(A) int(A.size())
#define PB push_back
#define MP(A, B) make_pair(A, B)
#define PTT pair<T, T>
#define fi first
#define se second

#define Rush for(int ____T=RD(); ____T--;)

#define Display(A, n, m) {                      \
	REP(i, n){		                            \
        REP(j, m) cout << A[i][j] << " ";       \
        cout << endl;				            \
	}						                    \
}

#define Display_1(A, n, m) {				    \
	REP_1(i, n){		                        \
        REP_1(j, m) cout << A[i][j] << " ";     \
		cout << endl;		            		\
	}						                    \
}

#pragma comment(linker, "/STACK:36777216")
//#pragma GCC optimize ("O2")
#define Ruby system("ruby main.rb")
#define Haskell system("runghc main.hs")
#define Python system("python main.py")
#define Pascal system("fpc main.pas")

typedef long long LL;
//typedef long double DB;
typedef double DB;
typedef unsigned UINT;
typedef unsigned long long ULL;

typedef vector<int> VI;
typedef vector<char> VC;
typedef vector<string> VS;
typedef vector<LL> VL;
typedef vector<DB> VF;
typedef set<int> SI;
typedef set<string> SS;
typedef map<int, int> MII;
typedef map<string, int> MSI;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
typedef vector<PII> VII;
typedef vector<VI> VVI;
typedef vector<VII> VVII;

template<class T> inline T& RD(T &);
template<class T> inline void OT(const T &);
inline LL RD(){LL x; return RD(x);}
inline DB& RF(DB &);
inline DB RF(){DB x; return RF(x);}
inline char* RS(char *s);
inline char& RC(char &c);
inline char RC();
inline char& RC(char &c){scanf(" %c", &c); return c;}
inline char RC(){char c; return RC(c);}
//inline char& RC(char &c){c = getchar(); return c;}
//inline char RC(){return getchar();}

template<class T> inline T& RDD(T &x){
    char c; for (c = getchar(); c < '-'; c = getchar());
    if (c == '-'){x = '0' - getchar(); for (c = getchar(); '0' <= c && c <= '9'; c = getchar()) x = x * 10 + '0' - c;}
    else {x = c - '0'; for (c = getchar(); '0' <= c && c <= '9'; c = getchar()) x = x * 10 + c - '0';}
    return x;
}

inline LL RDD(){LL x; return RDD(x);}

template<class T0, class T1> inline T0& RD(T0 &x0, T1 &x1){RD(x0), RD(x1); return x0;}
template<class T0, class T1, class T2> inline T0& RD(T0 &x0, T1 &x1, T2 &x2){RD(x0), RD(x1), RD(x2); return x0;}
template<class T0, class T1, class T2, class T3> inline T0& RD(T0 &x0, T1 &x1, T2 &x2, T3 &x3){RD(x0), RD(x1), RD(x2), RD(x3); return x0;}
template<class T0, class T1, class T2, class T3, class T4> inline T0& RD(T0 &x0, T1 &x1, T2 &x2, T3 &x3, T4 &x4){RD(x0), RD(x1), RD(x2), RD(x3), RD(x4); return x0;}
template<class T0, class T1, class T2, class T3, class T4, class T5> inline T0& RD(T0 &x0, T1 &x1, T2 &x2, T3 &x3, T4 &x4, T5 &x5){RD(x0), RD(x1), RD(x2), RD(x3), RD(x4), RD(x5); return x0;}
template<class T0, class T1, class T2, class T3, class T4, class T5, class T6> inline T0& RD(T0 &x0, T1 &x1, T2 &x2, T3 &x3, T4 &x4, T5 &x5, T6 &x6){RD(x0), RD(x1), RD(x2), RD(x3), RD(x4), RD(x5), RD(x6); return x0;}
template<class T0, class T1> inline void OT(const T0 &x0, const T1 &x1){OT(x0), OT(x1);}
template<class T0, class T1, class T2> inline void OT(const T0 &x0, const T1 &x1, const T2 &x2){OT(x0), OT(x1), OT(x2);}
template<class T0, class T1, class T2, class T3> inline void OT(const T0 &x0, const T1 &x1, const T2 &x2, const T3 &x3){OT(x0), OT(x1), OT(x2), OT(x3);}
template<class T0, class T1, class T2, class T3, class T4> inline void OT(const T0 &x0, const T1 &x1, const T2 &x2, const T3 &x3, const T4 &x4){OT(x0), OT(x1), OT(x2), OT(x3), OT(x4);}
template<class T0, class T1, class T2, class T3, class T4, class T5> inline void OT(const T0 &x0, const T1 &x1, const T2 &x2, const T3 &x3, const T4 &x4, const T5 &x5){OT(x0), OT(x1), OT(x2), OT(x3), OT(x4), OT(x5);}
template<class T0, class T1, class T2, class T3, class T4, class T5, class T6> inline void OT(const T0 &x0, const T1 &x1, const T2 &x2, const T3 &x3, const T4 &x4, const T5 &x5, const T6 &x6){OT(x0), OT(x1), OT(x2), OT(x3), OT(x4), OT(x5), OT(x6);}
inline char& RC(char &a, char &b){RC(a), RC(b); return a;}
inline char& RC(char &a, char &b, char &c){RC(a), RC(b), RC(c); return a;}
inline char& RC(char &a, char &b, char &c, char &d){RC(a), RC(b), RC(c), RC(d); return a;}
inline char& RC(char &a, char &b, char &c, char &d, char &e){RC(a), RC(b), RC(c), RC(d), RC(e); return a;}
inline char& RC(char &a, char &b, char &c, char &d, char &e, char &f){RC(a), RC(b), RC(c), RC(d), RC(e), RC(f); return a;}
inline char& RC(char &a, char &b, char &c, char &d, char &e, char &f, char &g){RC(a), RC(b), RC(c), RC(d), RC(e), RC(f), RC(g); return a;}
inline DB& RF(DB &a, DB &b){RF(a), RF(b); return a;}
inline DB& RF(DB &a, DB &b, DB &c){RF(a), RF(b), RF(c); return a;}
inline DB& RF(DB &a, DB &b, DB &c, DB &d){RF(a), RF(b), RF(c), RF(d); return a;}
inline DB& RF(DB &a, DB &b, DB &c, DB &d, DB &e){RF(a), RF(b), RF(c), RF(d), RF(e); return a;}
inline DB& RF(DB &a, DB &b, DB &c, DB &d, DB &e, DB &f){RF(a), RF(b), RF(c), RF(d), RF(e), RF(f); return a;}
inline DB& RF(DB &a, DB &b, DB &c, DB &d, DB &e, DB &f, DB &g){RF(a), RF(b), RF(c), RF(d), RF(e), RF(f), RF(g); return a;}
inline void RS(char *s1, char *s2){RS(s1), RS(s2);}
inline void RS(char *s1, char *s2, char *s3){RS(s1), RS(s2), RS(s3);}
template<class T0,class T1>inline void RDD(const T0&a, const T1&b){RDD(a),RDD(b);}
template<class T0,class T1,class T2>inline void RDD(const T0&a, const T1&b, const T2&c){RDD(a),RDD(b),RDD(c);}

template<class T> inline void RST(T &A){memset(A, 0, sizeof(A));}
template<class T> inline void FLC(T &A, int x){memset(A, x, sizeof(A));}
template<class T> inline void CLR(T &A){A.clear();}

template<class T0, class T1> inline void RST(T0 &A0, T1 &A1){RST(A0), RST(A1);}
template<class T0, class T1, class T2> inline void RST(T0 &A0, T1 &A1, T2 &A2){RST(A0), RST(A1), RST(A2);}
template<class T0, class T1, class T2, class T3> inline void RST(T0 &A0, T1 &A1, T2 &A2, T3 &A3){RST(A0), RST(A1), RST(A2), RST(A3);}
template<class T0, class T1, class T2, class T3, class T4> inline void RST(T0 &A0, T1 &A1, T2 &A2, T3 &A3, T4 &A4){RST(A0), RST(A1), RST(A2), RST(A3), RST(A4);}
template<class T0, class T1, class T2, class T3, class T4, class T5> inline void RST(T0 &A0, T1 &A1, T2 &A2, T3 &A3, T4 &A4, T5 &A5){RST(A0), RST(A1), RST(A2), RST(A3), RST(A4), RST(A5);}
template<class T0, class T1, class T2, class T3, class T4, class T5, class T6> inline void RST(T0 &A0, T1 &A1, T2 &A2, T3 &A3, T4 &A4, T5 &A5, T6 &A6){RST(A0), RST(A1), RST(A2), RST(A3), RST(A4), RST(A5), RST(A6);}
template<class T0, class T1> inline void FLC(T0 &A0, T1 &A1, int x){FLC(A0, x), FLC(A1, x);}
template<class T0, class T1, class T2> inline void FLC(T0 &A0, T1 &A1, T2 &A2, int x){FLC(A0, x), FLC(A1, x), FLC(A2, x);}
template<class T0, class T1, class T2, class T3> inline void FLC(T0 &A0, T1 &A1, T2 &A2, T3 &A3, int x){FLC(A0, x), FLC(A1, x), FLC(A2, x), FLC(A3, x);}
template<class T0, class T1, class T2, class T3, class T4> inline void FLC(T0 &A0, T1 &A1, T2 &A2, T3 &A3, T4 &A4, int x){FLC(A0, x), FLC(A1, x), FLC(A2, x), FLC(A3, x), FLC(A4, x);}
template<class T0, class T1, class T2, class T3, class T4, class T5> inline void FLC(T0 &A0, T1 &A1, T2 &A2, T3 &A3, T4 &A4, T5 &A5, int x){FLC(A0, x), FLC(A1, x), FLC(A2, x), FLC(A3, x), FLC(A4, x), FLC(A5, x);}
template<class T0, class T1, class T2, class T3, class T4, class T5, class T6> inline void FLC(T0 &A0, T1 &A1, T2 &A2, T3 &A3, T4 &A4, T5 &A5, T6 &A6, int x){FLC(A0, x), FLC(A1, x), FLC(A2, x), FLC(A3, x), FLC(A4, x), FLC(A5, x), FLC(A6, x);}
template<class T> inline void CLR(priority_queue<T, vector<T>, less<T> > &Q){while (!Q.empty()) Q.pop();}
template<class T> inline void CLR(priority_queue<T, vector<T>, greater<T> > &Q){while (!Q.empty()) Q.pop();}
template<class T0, class T1> inline void CLR(T0 &A0, T1 &A1){CLR(A0), CLR(A1);}
template<class T0, class T1, class T2> inline void CLR(T0 &A0, T1 &A1, T2 &A2){CLR(A0), CLR(A1), CLR(A2);}
template<class T0, class T1, class T2, class T3> inline void CLR(T0 &A0, T1 &A1, T2 &A2, T3 &A3){CLR(A0), CLR(A1), CLR(A2), CLR(A3);}
template<class T0, class T1, class T2, class T3, class T4> inline void CLR(T0 &A0, T1 &A1, T2 &A2, T3 &A3, T4 &A4){CLR(A0), CLR(A1), CLR(A2), CLR(A3), CLR(A4);}
template<class T0, class T1, class T2, class T3, class T4, class T5> inline void CLR(T0 &A0, T1 &A1, T2 &A2, T3 &A3, T4 &A4, T5 &A5){CLR(A0), CLR(A1), CLR(A2), CLR(A3), CLR(A4), CLR(A5);}
template<class T0, class T1, class T2, class T3, class T4, class T5, class T6> inline void CLR(T0 &A0, T1 &A1, T2 &A2, T3 &A3, T4 &A4, T5 &A5, T6 &A6){CLR(A0), CLR(A1), CLR(A2), CLR(A3), CLR(A4), CLR(A5), CLR(A6);}
template<class T> inline void CLR(T &A, int n){REP(i, n) CLR(A[i]);}

template<class T> inline T& SRT(T &A){sort(ALL(A)); return A;}
template<class T, class C> inline T& SRT(T &A, C B){sort(ALL(A), B); return A;}
template<class T> inline T& UNQ(T &A){A.resize(unique(ALL(SRT(A)))-A.begin());return A;}

//}

/** Constant List .. **/ //{

const int dx4[] = {-1, 0, 1, 0};
const int dy4[] = {0, 1, 0, -1};

const int dx8[] = {-1, 0, 1, 0 , -1 , -1 , 1 , 1};
const int dy8[] = {0, 1, 0, -1 , -1 , 1 , -1 , 1};

const int dxhorse[] = {-2 , -2 , -1 , -1 , 1 , 1 , 2 , 2};
const int dyhorse[] = {1 ,  -1 , 2  , -2 , 2 ,-2 , 1 ,-1};

const int MOD = 1000000007;
//int MOD = 99990001;
const int INF = 0x3f3f3f3f;
const LL INFF = 1LL << 60;
const DB EPS = 1e-9;
const DB OO = 1e15;
const DB PI = acos(-1.0); //M_PI;

//}

/** Add On .. **/ //{
// <<= '0. Nichi Joo ., //{
template<class T> inline void checkMin(T &a,const T b){if (b<a) a=b;}
template<class T> inline void checkMax(T &a,const T b){if (a<b) a=b;}
template<class T> inline void checkMin(T &a, T &b, const T x){checkMin(a, x), checkMin(b, x);}
template<class T> inline void checkMax(T &a, T &b, const T x){checkMax(a, x), checkMax(b, x);}
template <class T, class C> inline void checkMin(T& a, const T b, C c){if (c(b,a)) a = b;}
template <class T, class C> inline void checkMax(T& a, const T b, C c){if (c(a,b)) a = b;}
template<class T> inline T min(T a, T b, T c){return min(min(a, b), c);}
template<class T> inline T max(T a, T b, T c){return max(max(a, b), c);}
template<class T> inline T min(T a, T b, T c, T d){return min(min(a, b), min(c, d));}
template<class T> inline T max(T a, T b, T c, T d){return max(max(a, b), max(c, d));}
template<class T> inline T sqr(T a){return a*a;}
template<class T> inline T cub(T a){return a*a*a;}
inline int ceil(int x, int y){return (x - 1) / y + 1;}
inline int sgn(DB x){return x < -EPS ? -1 : x > EPS;}
inline int sgn(DB x, DB y){return sgn(x - y);}
//}
// <<= '1. Bitwise Operation ., //{
namespace BO{

inline bool _1(int x, int i){return bool(x&1<<i);}
inline bool _1(LL x, int i){return bool(x&1LL<<i);}
inline LL _1(int i){return 1LL<<i;}
inline LL _U(int i){return _1(i) - 1;};

inline int reverse_bits(int x){
    x = ((x >> 1) & 0x55555555) | ((x << 1) & 0xaaaaaaaa);
    x = ((x >> 2) & 0x33333333) | ((x << 2) & 0xcccccccc);
    x = ((x >> 4) & 0x0f0f0f0f) | ((x << 4) & 0xf0f0f0f0);
    x = ((x >> 8) & 0x00ff00ff) | ((x << 8) & 0xff00ff00);
    x = ((x >>16) & 0x0000ffff) | ((x <<16) & 0xffff0000);
    return x;
}

inline LL reverse_bits(LL x){
    x = ((x >> 1) & 0x5555555555555555LL) | ((x << 1) & 0xaaaaaaaaaaaaaaaaLL);
    x = ((x >> 2) & 0x3333333333333333LL) | ((x << 2) & 0xccccccccccccccccLL);
    x = ((x >> 4) & 0x0f0f0f0f0f0f0f0fLL) | ((x << 4) & 0xf0f0f0f0f0f0f0f0LL);
    x = ((x >> 8) & 0x00ff00ff00ff00ffLL) | ((x << 8) & 0xff00ff00ff00ff00LL);
    x = ((x >>16) & 0x0000ffff0000ffffLL) | ((x <<16) & 0xffff0000ffff0000LL);
    x = ((x >>32) & 0x00000000ffffffffLL) | ((x <<32) & 0xffffffff00000000LL);
    return x;
}

template<class T> inline bool odd(T x){return x&1;}
template<class T> inline bool even(T x){return !odd(x);}
template<class T> inline T low_bit(T x) {return x & -x;}
template<class T> inline T high_bit(T x) {T p = low_bit(x);while (p != x) x -= p, p = low_bit(x);return p;}
template<class T> inline T cover_bit(T x){T p = 1; while (p < x) p <<= 1;return p;}

} using namespace BO;//}
// <<= '2. Number Theory .,//{
namespace NT{
inline LL __lcm(LL a, LL b){return a*b/__gcd(a,b);}
inline void INC(int &a, int b){a += b; if (a >= MOD) a -= MOD;}
inline int sum(int a, int b){a += b; if (a >= MOD) a -= MOD; return a;}
inline void DEC(int &a, int b){a -= b; if (a < 0) a += MOD;}
inline int dff(int a, int b){a -= b; if (a < 0) a  += MOD; return a;}
inline void MUL(int &a, int b){a = (LL)a * b % MOD;}
inline int pdt(int a, int b){return (LL)a * b % MOD;}

inline int sum(int a, int b, int c){return sum(sum(a, b), c);}
inline int sum(int a, int b, int c, int d){return sum(sum(a, b), sum(c, d));}
inline int pdt(int a, int b, int c){return pdt(pdt(a, b), c);}
inline int pdt(int a, int b, int c, int d){return pdt(pdt(pdt(a, b), c), d);}

inline int pow(int a, int b){
    int c(1); while (b){
        if (b&1) MUL(c, a);
        MUL(a, a), b >>= 1;
    }
    return c;
}

inline int pow(int a, LL b){
    int c(1); while (b){
        if (b&1) MUL(c, a);
        MUL(a, a), b >>= 1;
    }
    return c;
}

template<class T> inline T pow(T a, LL b){
    T c(1); while (b){
        if (b&1) c *= a;
        a *= a, b >>= 1;
    }
    return c;
}

inline int _I(int b){
    int a = MOD, x1 = 0, x2 = 1, q;
    while (true){
        q = a / b, a %= b;
        if (!a) return (x2 + MOD) % MOD;
        DEC(x1, pdt(q, x2));

        q = b / a, b %= a;
        if (!b) return (x1 + MOD) % MOD;
        DEC(x2, pdt(q, x1));
    }
}

inline void DIV(int &a, int b){MUL(a, _I(b));}
inline int qtt(int a, int b){return pdt(a, _I(b));}

inline int phi(int n){
    int res = n; for (int i=2;sqr(i)<=n;++i) if (!(n%i)){
        DEC(res, qtt(res, i));
        do{n /= i;} while(!(n%i));
    }
    if (n != 1)
        DEC(res, qtt(res, n));
    return res;
}

};// using namespace NT;//}
//}

/** Miscellaneous .. **/ //{

/** Algorithm    .. */ //{
// <<= '-. Math .,//{
namespace Math{
	typedef long long typec;
	///Lib functions
	typec GCD(typec a, typec b)
	{
		return b ? GCD(b, a % b) : a;
	}
	typec extendGCD(typec a, typec b, typec& x, typec& y)
	{
		if(!b) return x = 1, y = 0, a;
		typec res = extendGCD(b, a % b, x, y), tmp = x;
		x = y, y = tmp - (a / b) * y;
		return res;
	}
	///for x^k
	typec power(typec x, typec k)
	{
		typec res = 1;
		while(k)
		{
			if(k&1) res *= x;
			x *= x, k >>= 1;
		}
		return res;
	}
	///for x^k mod m
	typec powerMod(typec x, typec k, typec m)
	{
		typec res = 1;
		while(x %= m, k)
		{
			if(k&1) res *= x, res %= m;
			x *= x, k >>=1;
		}
		return res;
	}
	/***************************************
	Inverse in mod p^t system
	***************************************/
	typec inverse(typec a, typec p, typec t = 1)
	{
		typec pt = power(p, t);
		typec x, y;
	    y = extendGCD(a, pt, x, y);
		return x < 0 ? x += pt : x;
	}
	/***************************************
	Linear congruence theorem
	x = a (mod p)
	x = b (mod q)
	for gcd(p, q) = 1, 0 <= x < pq
	***************************************/
	typec linearCongruence(typec a, typec b, typec p, typec q)
	{
		typec x, y;
		y = extendGCD(p, q, x, y);
		while(b < a) b += q / y;
		x *= b - a, x = p * x + a, x %= p * q;
		if(x < 0) x += p * q;
		return x;
	}
	/***************************************
	prime table
	O(n)
	***************************************/
	const int PRIMERANGE = 1000000;
	int prime[PRIMERANGE + 1];
	int mobius[PRIMERANGE + 1];
	int getPrime()
	{
		memset (prime, 0, sizeof (int) * (PRIMERANGE + 1));
		memset(mobius , 0 , sizeof(mobius));
		mobius[1] = 1;
		for (int i = 2; i <= PRIMERANGE; i++)
		{
			if (!prime[i]) prime[++prime[0]] = i , mobius[i] = -1;
			for (int j = 1; j <= prime[0] && prime[j] <= PRIMERANGE / i; j++)
			{
				prime[prime[j]*i] = 1;
				if (i % prime[j] == 0) break;
				else mobius[i * prime[j]] = -mobius[i];
			}
		}
		return prime[0];
	}
	/***************************************
	get factor of n
	O(sqrt(n))
	factor[][0] is prime factor
	factor[][1] is factor generated by this prime
	factor[][2] is factor counter

	need: Prime Table
	***************************************/
	///you should init the prime table before
	int factor[100][3], facCnt;
	int getFactors(int x)
	{
		facCnt = 0;
		int tmp = x;
		for(int i = 1; prime[i] <= tmp / prime[i]; i++)
		{
			factor[facCnt][1] = 1, factor[facCnt][2] = 0;
			if(tmp % prime[i] == 0)
				factor[facCnt][0] = prime[i];
			while(tmp % prime[i] == 0)
				factor[facCnt][2]++, factor[facCnt][1] *= prime[i], tmp /= prime[i];
			if(factor[facCnt][1] > 1) facCnt++;
		}
		if(tmp != 1)
			factor[facCnt][0] = tmp, factor[facCnt][1] = tmp, factor[facCnt++][2] = 1;
		return facCnt;
	}
	typec combinationModP(typec n, typec k, typec p)
	{
		if(k > n) return 0;
		if(n - k < k) k = n - k;
		typec a = 1, b = 1, x, y;
		int pcnt = 0;
		for(int i = 1; i <= k; i++)
		{
			x = n - i + 1, y = i;
			while(x % p == 0) x /= p, pcnt++;
			while(y % p == 0) y /= p, pcnt--;
			x %= p, y %= p, a *= x, b *= y;
			b %= p, a %= p;
		}
		if(pcnt) return 0;
		extendGCD(b, p, x, y);
		if(x < 0) x += p;
		a *= x, a %= p;
		return a;
	}
};//using namespace Math;
//}
// <<= '-. Geo ,.//{
namespace Geo{
	#define typec double
    const typec eps=1e-9;
int dblcmp(double d)
{
    return d < -eps ? -1 : d > eps;
}
inline double sqr(double x){return x*x;}
struct point
{
    double x,y;
    point(){}
    point(double _x,double _y):
    x(_x),y(_y){};
    void input()
    {
        scanf("%lf%lf",&x,&y);
    }
    void output()
    {
        printf("%.2f %.2f\n",x,y);
    }
    bool operator==(point a)const
    {
        return dblcmp(a.x-x)==0&&dblcmp(a.y-y)==0;
    }
    bool operator<(point a)const
    {
        return dblcmp(a.x-x)==0?dblcmp(y-a.y)<0:x<a.x;
    }
    double len()
    {
        return hypot(x,y);
    }
    double len2()
    {
        return x*x+y*y;
    }
    double distance(point p)
    {
        return hypot(x-p.x,y-p.y);
    }
    double distance2(point p)
    {
        return sqr(x-p.x)+sqr(y-p.y);
    }
    point add(point p)
    {
        return point(x+p.x,y+p.y);
    }
    point operator + (const point & p) const{
        return point(x+p.x,y+p.y);
    }
    point sub(point p)
    {
        return point(x-p.x,y-p.y);
    }
    point operator - (const point & p) const{
        return point(x-p.x,y-p.y);
    }
    point mul(double b)
    {
        return point(x*b,y*b);
    }
    point div(double b)
    {
        return point(x/b,y/b);
    }
    double dot(point p)
    {
        return x*p.x+y*p.y;
    }
    double operator * (const point & p) const{
        return x*p.x+y*p.y;
    }
    double det(point p)
    {
        return x*p.y-y*p.x;
    }
    double operator ^ (const point & p) const{
        return x*p.y-y*p.x;
    }
    double rad(point a,point b)
    {
    	point p=*this;
    	return fabs(atan2(fabs(a.sub(p).det(b.sub(p))),a.sub(p).dot(b.sub(p))));
	}
    point trunc(double r)
	{
		double l=len();
		if (!dblcmp(l))return *this;
		r/=l;
		return point(x*r,y*r);
	}
    point rotleft()
    {
        return point(-y,x);
    }
    point rotright()
    {
        return point(y,-x);
    }
    point rotate(point p,double angle)//�Ƶ�p��ʱ����תangle�Ƕ�
    {
        point v=this->sub(p);
        double c=cos(angle),s=sin(angle);
        return point(p.x+v.x*c-v.y*s,p.y+v.x*s+v.y*c);
    }
#undef typec
};
};//using namespace Geo;
//}
//}

/** I/O Accelerator Interface .. **/ //{
template<class T> inline T& RD(T &x){
    //cin >> x;
    //scanf("%d", &x);
    char c; for (c = getchar(); c < '0'; c = getchar()); x = c - '0'; for (c = getchar(); '0' <= c && c <= '9'; c = getchar()) x = x * 10 + c - '0';
    //char c; c = getchar(); x = c - '0'; for (c = getchar(); c >= '0'; c = getchar()) x = x * 10 + c - '0';
    return x;
}

inline DB& RF(DB &x){
    //cin >> x;
    scanf("%lf", &x);
    /*char t; while ((t=getchar())==' '||t=='\n'); x = t - '0';
    while ((t=getchar())!=' '&&t!='\n'&&t!='.')x*=10,x+=t-'0';
    if (t=='.'){DB l=1; while ((t=getchar())!=' '&&t!='\n')l*=0.1,x += (t-'0')*l;}*/
    return x;
}

inline char* RS(char *s){
    //gets(s);
    scanf("%s", s);
    return s;
}

int Case; template<class T> inline void OT(const T &x){
    //printf("Case %d: %d\n", ++Case, x);
    //printf("%.2lf\n", x);
    //printf("%d\n", x);
    cout << x << endl;
}

Which is the best data structure to implement a graph on?

Excuse me, how can I generate large inputs to hack solutions?

I and trying to find a good book to read (on programming). Which book do you recommend?

I'm just wondering, how fast should my algorithm be in order to avoid TLE (Time Limit Exceeded)?