| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 164 |
| 3 | Dominater069 | 161 |
| 4 | Um_nik | 159 |
| 5 | atcoder_official | 157 |
| 6 | djm03178 | 154 |
| 7 | adamant | 153 |
| 8 | luogu_official | 149 |
| 9 | awoo | 148 |
| 10 | TheScrasse | 146 |
Authors of today's contest are Artem Rakhov and me. Thanks to Mike Mirzayanov, Edvard Davtyan and Julia Satushina for help in the organisation.
I hope, you will have fun.
Good luck!
P.S. After start of the contest, you can download the statements:
UPD. The contest has finished and you can see the standings and tasks. The winner and only participant who has solved all the problems is kalinov. Congratulations!
You may read complete rules here.

The text contains only preliminary rules of Codeforces contests — something surely will change. In particular, I hope to help the community to find the illogic in the rules. However, I have already discussed the format with programming contests dinosaurs and made unrated alpha contests — it seems rules are OK.
I think than the format 5 tasks x 2 hour is quite good. For this reason, in the near future we will not change it, but of course, experiments are possible.
1. Before the competition all participants are divided into rooms, each room contains about 20 participants. For now random strategy works, but after a while it will be somehow correlated with the rating.
Problem А. Triangle
Pythagorean theorem, brute force
In this problem you should implement a function, which takes three points and checks whether they form a right-angled triangle. There are a lot of ways to do so, but the simplest one is using a Pythagorean theorem.
Welcome to Codeforces Beta Round #18
Authors of today's contest are Mike Mirzayanov, Edvard Davtyan and me. Thanks to Dmitry Matov for his help in statements preparation and Julia Satushina for translation of problems in English.
Good luck everyone!
- Problems
- Final standings
- Contest winner: I_am_Feeling_Lucky
Problem A. Noldbach problem
To solve this problem you were to find prime numbers in range [2..N]. The constraints were pretty small, so you could do that in any way - using the Sieve of Eratosthenes or simply looping over all possible divisors of a number.
Take every pair of neighboring prime numbers and check if their sum increased by 1 is a prime number too. Count the number of these pairs, compare it to K and output the result.
Problem B. Hierarchy
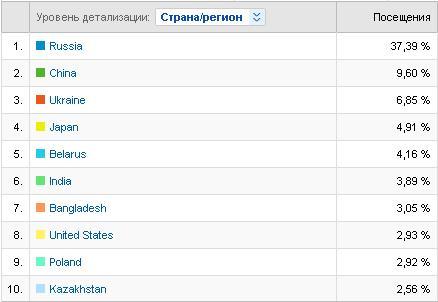
This post contains few words and many pictures. I decided to publish statistics on Codeforces visitors for the past two months. Why? I believe that it might be interesting. I took pictures from Google Analitycs.
Codeforces was born little more than 4 months ago. During this time, we held 16 contests (though one of them was non-rated). There are more than 4000 registered users, and every day we get about 30 more. There are 1797 coders participated in the contests, many of them participate in our contests regularly. The average number of registrations for one competition is growing, and I want to believe that soon it will conquer psychological barrier 1000 users. Also codeforces social network is popular: more than 400 posts, almost 6000 comments. The leader of the hit parade of posts is this post, has collected to date 184 comments. Bravo, SkidanovAlex! And of course I say thank you to everyone who helped make the project: those who help in the development, who make the problems, translate texts and write the alternative solutions, participate in community life, and just take part in contests. Thank you!
Below you will find a few more pictures and statistics, the total traffic of about 250KB.
Good afternoon.
Today I am the author of problems. I want to thank the creator of Codeforces Mike Mirzayanov and Edvard Davtyan for assistance in the problems preparation and Julia Satushina for great translations into English.
I wish everyone advance to the first division!
Artem Rakhov
UPD: The contest is over, thank you all for participating!
- Problems
- Final standings
- Contest winner: krijgertje
| Name |
|---|










