| Codeforces Global Round 1 |
|---|
| Закончено |
Определим эйлеров обход дерева (связного неориентированного графа без циклов) следующим образом: рассмотрим рекурсивный алгоритм поиска в глубину, который обходит вершины дерева и нумерует вершины в том порядке, в котором их посещает, при этом учитывается только первое посещение каждой вершины. Данная функция стартует из вершины с номером $$$1$$$, а затем рекурсивно вызывается от всех вершин, которые соединены ребром с текущей и ещё не посещены, в порядке возрастания номеров вершин. Формально данную функцию можно описать так:
next_id = 1
id = массив длины n, заполненный -1
visited = массив длины n, заполненный false
function dfs(v):
visited[v] = true
id[v] = next_id
next_id += 1
for to по соседям v в порядке возрастания:
if not visited[to]:
dfs(to)
Дано взвешенное дерево, вершины которого пронумеровали в порядке эйлерова обхода целыми числами от $$$1$$$ до $$$n$$$ при помощи алгоритма, описанного выше.
Назовём листом вершину дерева, соединённую ребром ровно с одной другой вершиной. В данном вам дереве вершина $$$1$$$ не является листом. Расстоянием между двумя вершинами дерева назовём сумму весов рёбер на единственном простом пути между ними.
Требуется ответить на $$$q$$$ запросов следующего вида: по заданным числам $$$v$$$, $$$l$$$ и $$$r$$$ сообщить кратчайшее расстояние от вершины $$$v$$$ до одного из листов дерева, имеющего номер от $$$l$$$ до $$$r$$$ (включительно).
В первой строке даны два целых числа $$$n$$$ и $$$q$$$ ($$$3 \leq n \leq 500\,000, 1 \leq q \leq 500\,000$$$) — количество вершин в дереве и количество запросов соответственно.
Следующие $$$n - 1$$$ строк задают рёбра дерева: $$$(i - 1)$$$-я строка содержит два целых числа $$$p_i$$$ и $$$w_i$$$ ($$$1 \leq p_i < i, 1 \leq w_i \leq 10^9$$$), обозначающие ребро между вершинами $$$p_i$$$ и $$$i$$$ с весом $$$w_i$$$.
Гарантируется, что заданные рёбра задают дерево, вершины которого пронумерованы в порядке эйлерова обхода, и что вершина с номером $$$1$$$ не является листом.
Следующие $$$q$$$ строк содержат описания запросов. Каждая из них содержит три целых числа $$$v_i$$$, $$$l_i$$$, $$$r_i$$$ ($$$1 \leq v_i \leq n, 1 \leq l_i \leq r_i \leq n$$$), обозначающие параметры запроса, описанные в условии. Гарантируется, что существует хотя бы один лист с номером $$$x$$$ такой, что $$$l_i \leq x \leq r_i$$$.
Выведите $$$q$$$ чисел — ответы на запросы в порядке, в котором они заданы во входных данных.
5 3 1 10 1 1 3 2 3 3 1 1 5 5 4 5 4 1 2
3 0 13
5 3 1 1000000000 2 1000000000 1 1000000000 1 1000000000 3 4 5 2 1 5 2 4 5
3000000000 1000000000 2000000000
11 8 1 7 2 1 1 20 1 2 5 6 6 2 6 3 5 1 9 10 9 11 5 1 11 1 1 4 9 4 8 6 1 4 9 7 11 9 10 11 8 1 11 11 4 5
8 8 9 16 9 10 0 34
В первом примере дерево выглядит так:
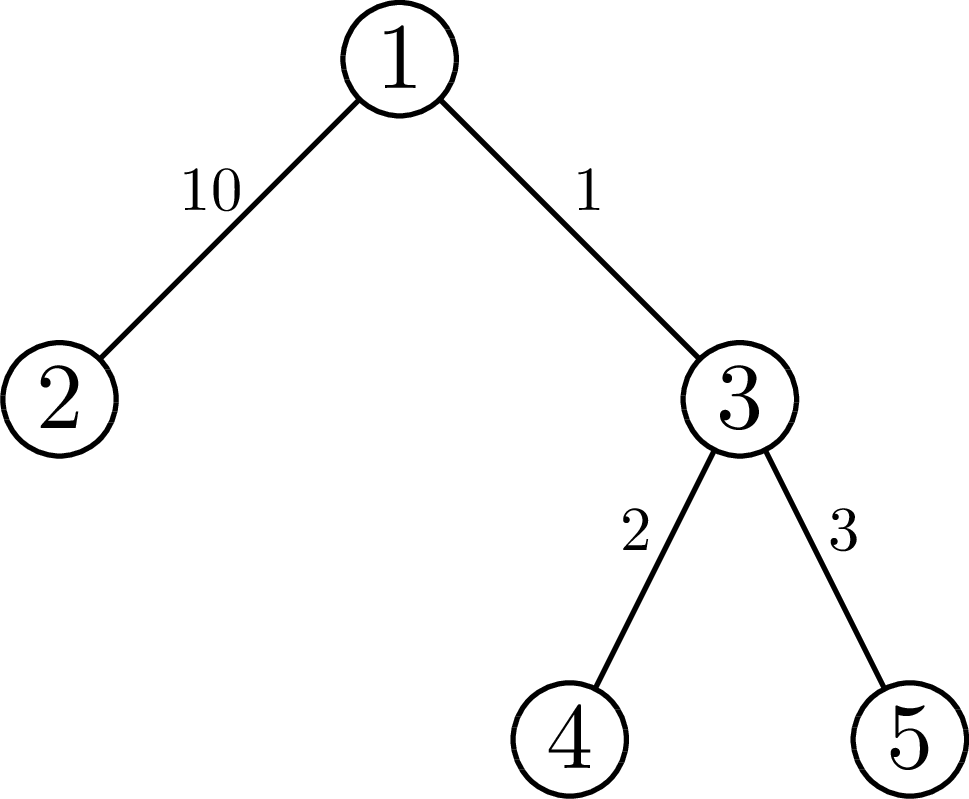
В первом запросе ближайший к вершине $$$1$$$ лист имеет номер $$$4$$$. Расстояние до него равно $$$3$$$. Во втором запросе ближайшим к вершине $$$5$$$ листом является вершина с номером $$$5$$$, расстояние до которой равно $$$0$$$. В третьем примере ближайшим к вершине $$$4$$$ листом является вершина с номером $$$4$$$, однако она не попадает в отрезок вершин $$$[1, 2]$$$ запроса. Единственным листом с номером, попадающим в отрезок $$$[1, 2]$$$ является вершина с номером $$$2$$$, расстояние до которой от вершины $$$4$$$ равно $$$13$$$.
| Название |
|---|




