| Codeforces Round 582 (Div. 3) |
|---|
| Закончено |
Вам задано взвешенное дерево, состоящее из $$$n$$$ вершин. Напомним, что деревом называется связный граф без циклов. Вершины $$$u_i$$$ и $$$v_i$$$ соединены ребром веса $$$w_i$$$.
Вам задано $$$m$$$ запросов. $$$i$$$-й запрос задан целым числом $$$q_i$$$. В этом запросе вам необходимо посчитать количество пар вершин $$$(u, v)$$$ ($$$u < v$$$) таких, что максимальный вес ребра на простом пути между $$$u$$$ и $$$v$$$ не превосходит $$$q_i$$$.
Первая строка входных данных содержит два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n, m \le 2 \cdot 10^5$$$) — количество вершин в дереве и количество запросов.
Каждая из следующих $$$n - 1$$$ строк описывает ребра дерева. Ребро $$$i$$$ обозначается тремя целыми числами $$$u_i$$$, $$$v_i$$$ и $$$w_i$$$ — номерами вершин, которые оно соединяет ($$$1 \le u_i, v_i \le n$$$, $$$u_i \ne v_i$$$) и весом ребра ($$$1 \le w_i \le 2 \cdot 10^5$$$). Гарантируется, что заданный набор ребер образует дерево.
Последняя строка входных данных содержит $$$m$$$ целых чисел $$$q_1, q_2, \dots, q_m$$$ ($$$1 \le q_i \le 2 \cdot 10^5$$$), где $$$q_i$$$ равно максимальному весу ребра в $$$i$$$-м запросе.
Выведите $$$m$$$ целых чисел — ответы на запросы. $$$i$$$-е число должно равняться количеству пар вершин $$$(u, v)$$$ ($$$u < v$$$) таких, что максимальный вес ребра на простом пути между $$$u$$$ и $$$v$$$ не превосходит $$$q_i$$$.
Запросы пронумерованы от $$$1$$$ до $$$m$$$ в порядке входных данных.
7 5 1 2 1 3 2 3 2 4 1 4 5 2 5 7 4 3 6 2 5 2 3 4 1
21 7 15 21 3
1 2 1 2
0 0
3 3 1 2 1 2 3 2 1 3 2
1 3 3
Картинка, соответствующая дереву из первого тестового примера: 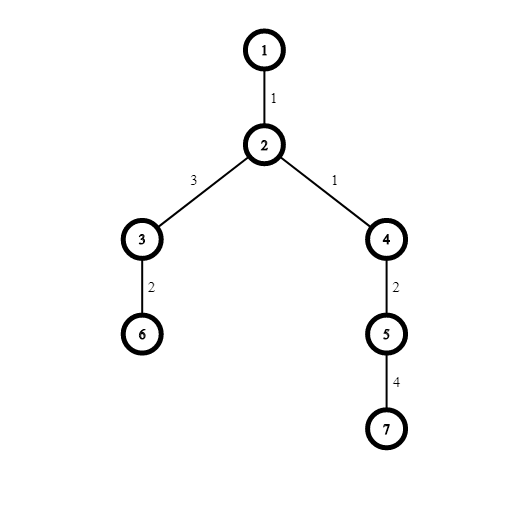
| Название |
|---|




