| Технокубок 2022 - Отборочный Раунд 1 |
|---|
| Закончено |
Даже если вы просто оставите их в покое, они разлетятся на куски сами по себе. Значит, кто-то должен их защищать, верно?
Вы снова играете с Тьюсером в городе Лиюэ. Водя эксцентричного малыша по городу, вы заметили кое-что интересное в его структуре.
Лиюэ можно представить в виде направленного графа, содержащего $$$n$$$ вершин. Вершины пронумерованы от $$$1$$$ до $$$n$$$. Ребро из вершины $$$a$$$ в вершину $$$b$$$ существует тогда и только тогда, когда $$$a < b$$$.
Путь между вершинами $$$a$$$ и $$$b$$$ определяется как последовательность ребер таких, можно начать путь в $$$a$$$, пройти по всем этим ребрам в соответствующем неправлении, и закончить в $$$b$$$. Длина пути равна количеству ребер. Радужный путь длины $$$x$$$ определяется как такой путь в графе, что среди этих $$$x$$$ ребер существует по крайней мере 2 разных цвета.
Любимое число Тьюсера — $$$k$$$. Вам интересно следующее: если вам нужно обозначить каждое ребро цветом, то какое минимальное количество цветов понадобится для того, чтобы все пути длины $$$k$$$ или больше были радужными?
Тьюсер хочет удивить своего старшего брата картой Лиюэ. Он также хочет узнать допустимую раскраску ребер, которая использует минимальное количество цветов. Пожалуйста, помогите ему решить эту задачу!
Единственная строка ввода содержит два целых числа $$$n$$$ и $$$k$$$ ($$$2 \leq k < n \leq 1000$$$).
В первой строке выведите $$$c$$$, минимальное количество цветов, необходимое для выполнения вышеуказанных требований.
Во второй строке выведите допустимую раскраску ребер в виде массива из $$$\frac{n(n-1)}{2}$$$ целых чисел от $$$1$$$ до $$$c$$$. В ней должно присутствовать ровно $$$c$$$ различных цветов. Выведите ребра в порядке возрастания сначала по начальному вершине, затем по второй вершине.
Например, если $$$n=4$$$, то цвета ребер нужно выводить в таком порядке: ($$$1$$$, $$$2$$$), ($$$1$$$, $$$3$$$), ($$$1$$$, $$$4$$$), ($$$2$$$, $$$3$$$), ($$$2$$$, $$$4$$$), ($$$3$$$, $$$4$$$)
5 3
2 1 2 2 2 2 2 2 1 1 1
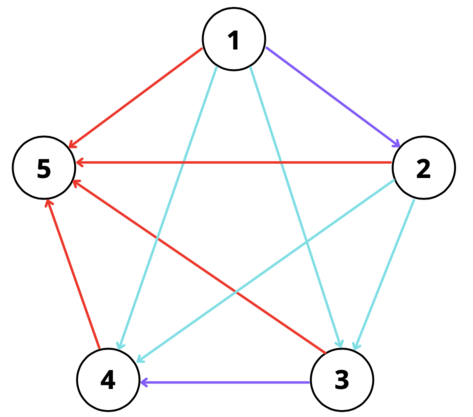
5 2
3 3 2 2 1 2 2 1 3 1 1
8 7
2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
3 2
2 1 2 2
Соответствующая конструкция для первого примера выглядит следующим образом:
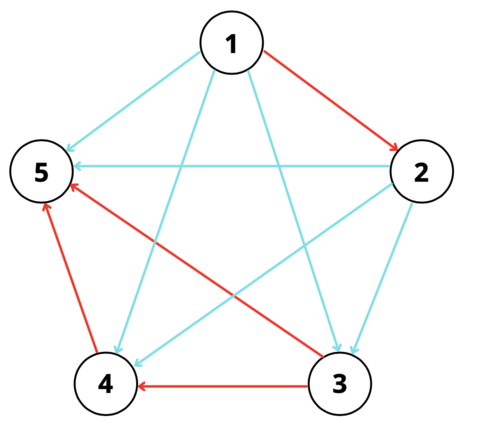
Соответствующая конструкция для второго примера выглядит следующим образом:
| Название |
|---|




