| Codeforces Round 883 (Div. 3) |
|---|
| Закончено |
Это простая версия задачи. Единственное отличие в том, что в этой версии $$$n \le 10^6$$$.
Однажды зимним утром Рудольф задумчиво смотрел в окно и наблюдал за падающими снежинками. Он очень быстро заметил некоторую симметрию в конфигурации снежинок. И как истинный математик, Рудольф придумал математическую модель снежинки.
Он определил снежинку как неориентированный граф, строящийся по следующим правилам:
- Изначально в графе одна единственная вершина.
- Далее в граф добавляются ещё вершины. Исходная вершина соединяется ребрами с ещё $$$k$$$ новыми вершинами ($$$k > 1$$$).
- Каждая из вершин, соединённая только с одной другой вершиной, соединяется ребрами с ещё $$$k$$$ новыми вершинами. Этот шаг нужно выполнить хотя бы один раз.
Минимальная снежинка для $$$k = 4$$$ приведена на рисунке.
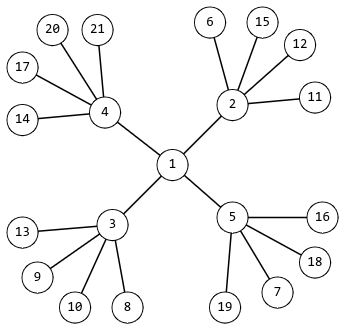
После некоторых математических изысканий Рудольф понял, что такие снежинки могут иметь далеко не любое число вершин. Помогите Рудольфу проверить, может ли существовать снежинка с $$$n$$$ вершинами.
В первой строке входных данных содержится целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных в тесте.
Далее следуют описания наборов.
В первой строке набора содержится целое число $$$n$$$ ($$$1 \le n \le 10^6$$$) — количество вершин, для которого нужно проверить существование снежинки.
Выведите $$$t$$$ строк, каждая из которых является ответом на соответствующий набор — «YES», если существует такое $$$k > 1$$$, для которого можно построить снежинку с заданным количеством вершин; «NO» в противном случае.
912361315255101011000000
NO NO NO NO YES YES YES YES NO
| Название |
|---|




