| Codeforces Round 906 (Div. 1) |
|---|
| Закончено |
Рассмотрим два неориентированных графа $$$G_1$$$ и $$$G_2$$$. Каждая вершина в $$$G_1$$$ и в $$$G_2$$$ имеет номер. Дореми называет $$$G_1$$$ и $$$G_2$$$ подобными тогда и только тогда, когда:
- Все номера в $$$G_1$$$ различны, и все номера в $$$G_2$$$ различны.
- Множество $$$S$$$ номеров в $$$G_1$$$ совпадает с множеством номеров в $$$G_2$$$.
- Для каждой пары двух различных номеров $$$u$$$ и $$$v$$$ в $$$S$$$ соответствующие вершины находятся в одной и той же компоненте связности в $$$G_1$$$ тогда и только тогда, когда они находятся в одной и той же компоненте связности в $$$G_2$$$.
Теперь Дореми дает вам два дерева $$$T_1$$$ и $$$T_2$$$ с $$$n$$$ вершинами, пронумерованными от $$$1$$$ до $$$n$$$. Вы можете выполнить следующую операцию любое количество раз:
- Выбрать множество ребер $$$E_1$$$ из $$$T_1$$$ и множество ребер $$$E_2$$$ из $$$T_2$$$, такие, что $$$\overline{E_1}$$$ и $$$\overline{E_2}$$$ подобны. Здесь $$$\overline{E}$$$ представляет собой граф, который задается набором рёбер $$$E$$$ из дерева $$$T$$$ и концами этих рёбер (т.е. подграф, индуцированный ребрами). Иными словами, $$$\overline{E}$$$ получается из $$$T$$$ удалением всех рёбер, не входящих в $$$E$$$, а также последующего удаления всех изолированных вершин.
- Поменяйте местами множество ребер $$$E_1$$$ в $$$T_1$$$ с множеством ребер $$$E_2$$$ в $$$T_2$$$.
Теперь Дореми интересно, сколько различных $$$T_1$$$ можно получить после любого количества операций. Можете ли вы помочь ей найти ответ? Выведите ответ по модулю $$$10^9+7$$$.
Входные данные состоят из нескольких наборов входных данных. Первая строка содержит одно целое число $$$t$$$ ($$$1\le t\le 2\cdot 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка содержит целое число $$$n$$$ ($$$2\le n\le 10^5$$$) — количество вершин в деревьях $$$T_1$$$ и $$$T_2$$$.
Каждая из следующих $$$n-1$$$ строк содержит два целых числа $$$u,v$$$ ($$$1\le u,v\le n$$$), представляющих собой неориентированное ребро в $$$T_1$$$. Гарантируется, что эти ребра образуют дерево.
Каждая из следующих $$$n-1$$$ строк содержит два целых числа $$$u,v$$$ ($$$1\le u,v\le n$$$), представляющих собой ненаправленное ребро в $$$T_2$$$. Гарантируется, что эти ребра образуют дерево.
Гарантируется, что сумма $$$n$$$ не превышает $$$2\cdot 10^5$$$.
Для каждого набора входных данных выведите одну строку с целым числом, представляющим собой количество отличий $$$T_1$$$ после любого количества операций по модулю $$$10^9+7$$$.
321 22 131 32 32 32 141 22 33 44 22 11 3
1 2 4
В первом наборе входных данных существует не более одного множества $$$T_1$$$, имеющего единственное ребро $$$(1,2)$$$.
Во втором наборе входных данных можно выбрать множество ребер $$$\{(1,3),(2,3)\}$$$ в $$$T_1$$$, множество ребер $$$\{(1,2),(2,3)\}$$$ в $$$T_2$$$ и поменять их местами. Таким образом, $$$T_1$$$ может быть $$$1-3-2$$$ или $$$1-2-3$$$.
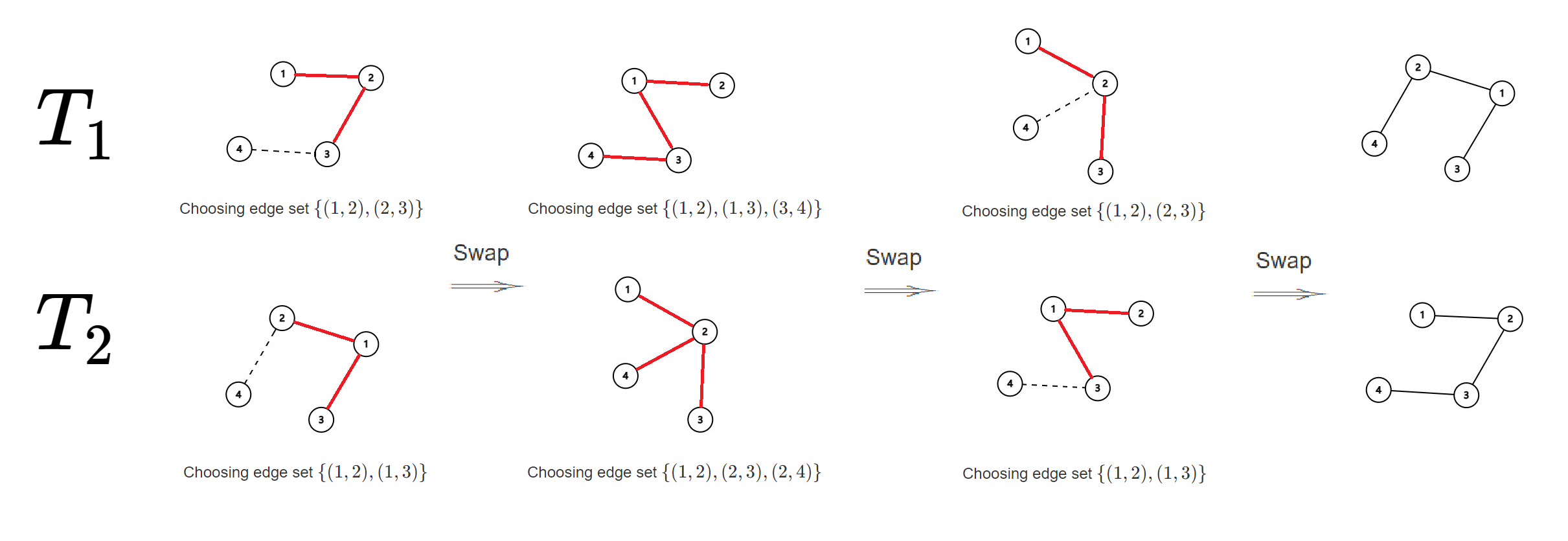
В третьем наборе входных данных существует $$$4$$$ различных $$$T_1$$$, как показано на следующих рисунках.
| Название |
|---|




