| Codeforces Round 124 (Div. 1) |
|---|
| Закончено |
Имеется прямоугольный лабиринт размером n × m клеток, каждая из которых либо проходима, либо является стеной (непроходима). Маленький мальчик нашел этот лабиринт и циклически замостил им плоскость таким образом, что плоскость стала бесконечным лабиринтом. Теперь клетка (x, y) этой плоскости является стеной тогда и только тогда, когда клетка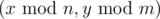 
является стеной.
Под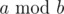 
в этой задаче понимается остаток от деления числа a на число b.
Маленький мальчик встал в некоторую клетку плоскости и интересуется, может ли он удалиться от своего стартового расположения на бесконечно большое расстояние. Из клетки (x, y) он может перемещаться в одну из клеток (x, y - 1), (x, y + 1), (x - 1, y) и (x + 1, y), если эта клетка не является стеной.
В первой строке записаны через пробел два целых числа n и m (1 ≤ n, m ≤ 1500) — высота и ширина лабиринта, которым маленький мальчик циклически замостил плоскость.
В следующих n строках записано по m символов — описание лабиринта. Каждый символ равен либо «#», что означает стену, либо «.», что означает проходимый участок, либо «S», что означает стартовую позицию маленького мальчика.
Стартовая позиция является проходимым участком. Гарантируется, что символ «S» присутствует во входных данных ровно один раз.
Выведите «Yes» (без кавычек), если маленький мальчик сможет удалиться от своего первоначального расположения на бесконечно большое расстояние, и «No» (без кавычек) иначе.
5 4
##.#
##S#
#..#
#.##
#..#
Yes
5 4
##.#
##S#
#..#
..#.
#.##
No
В первом примере маленький мальчик может бесконечно долго идти вверх, так как существует «сквозной» проход снизу вверх. Для этого надо бесконечно повторять последовательность шагов «вверх, вверх, влево, вверх, вверх, вправо, вверх».
Во втором примере проход снизу вверх закрыт. Выйти за пределы лабиринта влево тоже не получается — в следующей «копии» лабиринта маленький мальчик попадает в тупик.
