| Codeforces Round 277.5 (Div. 2) |
|---|
| Закончено |
Томаш постоянно плутает и теряется, гуляя по улицам столицы Берляндии. Еще бы, ведь он привык, что в его родном городе для любой пары перекрестков существует ровно один способ пройти от одного к другому. В столице Берляндии это совсем не так!
Томаш подметил, что даже простые случаи неоднозначности перемещения его путают. Так, четверку различных перекрестков a, b, c и d таких, что существует два пути из a в c — один через b, а другой через d, он называет «чёртов ромб». Обратите внимание, пары перекрёстков (a, b), (b, c), (a, d), (d, c) должны быть непосредственно соединены дорогами. Схематично «чёртов ромб» изображен на рисунке ниже:
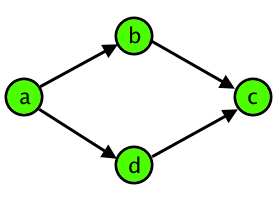
Наличие других дорог между любыми из перекрестков не делают ромб более привлекательным для Томаша, поэтому четверка перекрестков остается для него «чёртовым ромбом».
Принимая во внимание, что в столице Берляндии n перекрестков и m дорог, все из которых являются односторонними и известны наперед, найдите количество «чёртовых ромбов» в городе.
При сравнении ромбов порядок перекрестков b и d значения не имеет.
В первой строке входных данных записана пара целых чисел n, m (1 ≤ n ≤ 3000, 0 ≤ m ≤ 30000) — количество перекрестков и дорог соответственно. Далее в m строках перечислены дороги по одной в строке. Каждая из дорог задана парой целых чисел ai, bi (1 ≤ ai, bi ≤ n;ai ≠ bi) — номером перекрестка откуда она ведет и номером перекрестка куда она ведет. Между парой перекрестков существует не более одной дороги в каждом из двух направлений.
Не гарантируется, что из любого перекрестка можно добрать до любого другого.
Выведите искомое количество «чёртовых ромбов».
5 4
1 2
2 3
1 4
4 3
1
4 12
1 2
1 3
1 4
2 1
2 3
2 4
3 1
3 2
3 4
4 1
4 2
4 3
12
| Название |
|---|




