| Codeforces Round 283 (Div. 2) |
|---|
| Закончено |
Миша пытается заниматься скалолазанием, но получается у него из рук вон плохо.
На стене висят n зацепок, i-я из которых расположена на высоте ai от земли. Кроме того, пусть последовательность ai возрастает, т.е. ai < ai + 1 для всех i от 1 до n - 1; назовем такую последовательность трассой. Миша считает, что трасса a1, ..., an обладает сложностью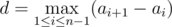 
. Иными словами, сложность равна максимальному расстоянию между соседними по высоте зацепками.
Сегодня Миша решил пролезть трассу, в которой зацепки висят на высотах a1, ..., an. Чтобы усложнить себе задачу, Миша решил снять одну из зацепок, т.е. удалить один элемент последовательности (например, если из последовательности (1, 2, 3, 4, 5) удалить третий элемент, останется последовательность (1, 2, 4, 5)). Однако, поскольку лазает Миша плохо, он хочет, чтобы после удаления сложность (т. е. максимальная разность высоты между соседними зацепками) была минимальной среди всех возможных вариантов снять одну зацепку. Первая и последняя зацепка должны остаться на месте.
Помогите Мише определить минимальную сложность трассы после снятия одной зацепки.
Первая строка содержит одно целое число n (3 ≤ n ≤ 100) — количество зацепок.
Следующая строка содержит n целых чисел ai (1 ≤ ai ≤ 1000), разделенных пробелами, где ai — высота, на которой висит зацепка номер i. Последовательность ai возрастает (т.е. каждый элемент, кроме первого, строго больше предыдущего).
Выведите одно число — минимальную сложность трассы после снятия одной зацепки.
3
1 4 6
5
5
1 2 3 4 5
2
5
1 2 3 7 8
4
В первом тесте можно удалить только вторую зацепку, после нее последовательность примет вид (1, 6), максимальная разность соседних элементов равна 5.
Во втором тесте после удаления любой зацепки сложность равна 2.
В третьем тесте можно получить последовательности (1, 3, 7, 8), (1, 2, 7, 8), (1, 2, 3, 8), для которых сложность составляет 4, 5 и 5 соответственно. Таким образом, ответ достигается при удалении второго элемента и равен 4.
