| Codeforces Round 283 (Div. 1) |
|---|
| Закончено |
Пусть sk(n) равно сумме цифр числа n в k-ичной системе счисления. Например, s2(5) = s2(1012) = 1 + 0 + 1 = 2, s3(14) = s3(1123) = 1 + 1 + 2 = 4.
Последовательность целых чисел a0, ..., an - 1 определяется соотношением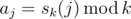 
. Требуется вычислить количество различных подпоследовательностей последовательности a0, ..., an - 1. Посчитайте остаток от деления ответа на 109 + 7.
Последовательность a1, ..., ak является подпоследовательностью последовательности b1, ..., bl, если существует последовательность индексов 1 ≤ i1 < ... < ik ≤ l, такая что a1 = bi1, ..., ak = bik. В частности, пустая последовательность (т.е. последовательность, состоящая из нуля элементов) является подпоследовательностью любой последовательности.
В первой строке записано два целых числа, разделенных пробелом, — n и k (1 ≤ n ≤ 1018, 2 ≤ k ≤ 30).
В единственной строке выведите остаток от деления ответа на задачу на 109 + 7.
4 2
11
7 7
128
В первом примере последовательность ai выглядит следующим образом: (0, 1, 1, 0). Все возможные подпоследовательности:
Во втором примере последовательность ai выглядит следующим образом: (0, 1, 2, 3, 4, 5, 6). Подпоследовательностями этой последовательности являются все возрастающие последовательности из чисел от 0 до 6 и только они. Легко видеть, что их ровно 27 = 128.
