| Codeforces Round 336 (Div. 1) |
|---|
| Закончено |
Геос и Сайтама пошли покупать новогодние ёлки, но их внимание привлекло необыкновенное Могучее Дерево. Могучее Дерево изначально состоит из единственной корневой вершины, имеющей номер 1. Могучее дерево иногда растёт благодаря волшебному феномену, известному как обновление. Во время обновления к дереву добавляется один новый лист. Каждой вершине дерева (корню и всем добавленным вершинам) присвоено некоторое значение vi. Мощность вершины определяется как сила мультимножества, составленного из значения данной вершины (то есть числа vi) и значений мощностей её непосредственных детей. Сила мультимножества определяется как сумма всех элементов в мультимножестве, умноженная на их количество, то есть для некоторого мультимножества S:
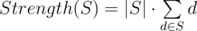
Первая строка входных данных содержит два числа v1 и q (1 ≤ v1 < 109, 1 ≤ q ≤ 200 000) — значение, ассоциированное с вершиной 1, и суммарное количество обновлений и запросов соответственно. В следующих q строках записаны обновления и запросы. Каждая строка имеет вид:
- 1 pi vi, если это обновление дерева. Добавляемая вершина получает в качестве номера минимальное положительное целое число, ещё не использующееся как номер какой-нибудь вершины. Гарантируется, что вершина с номером pi уже существует в дереве и что 1 ≤ vi < 109.
- формы 2 ui, если это вопрос Сайтама. Гарантируется, что вершина ui уже присутствует в дереве.
Для каждого запроса выведите мощность указанной вершины в данный момент по модулю 109 + 7.
2 5
1 1 3
1 2 5
1 3 7
1 4 11
2 1
344
5 5
1 1 4
1 2 3
2 2
1 2 7
2 1
14
94
В первом примере после всех обновлений дерево будет выглядеть следующим образом: 1 — 2 — 3 — 4 — 5
Вершинам будут присвоены следующие значения: 2 — 3 — 5 — 7 — 11
Мощности вершин будут, соответственно, равны: 344 — 170 — 82 — 36 — 11
| Название |
|---|




