| Codeforces Round 359 (Div. 1) |
|---|
| Закончено |
После того как Каю в глаз попал осколок дьявольского зеркала, его уже не трогала красота роз. Зато он начал любоваться снежинками.
Однажды в сад прилетела большая снежинка, имеющая форму корневого дерева (связного графа без циклов) на n вершинах. Корнем дерева является вершина номер 1. Кай очень заинтересовался его структурой.
После долгого изучения Каю стали интересны ответы на некоторые запросы про q вершин. А именно: для i-го запроса ему интересно, какой номер имеет центроид поддерева vi-й вершины.
Ваша задача — ответить на все запросы Кая.
Поддеревом вершины называется часть дерева, состояющая из этой вершины, а также всех её потомков. Другими словами, поддерево вершины v состоит из таких вершин u, что v обязательно присутствует на пути от u до корня дерева.
Центроидом дерева называется вершина, при удалении которой дерево развалится на компоненты связности, каждая из которых не превосходит по количеству вершин половину числа вершин исходного дерева.
В первой строке входных данных записаны два числа n и q (2 ≤ n ≤ 300 000, 1 ≤ q ≤ 300 000) — размер исходного дерева и количество запросов соответственно.
Во второй строке записаны n - 1 число p2, p3, ..., pn (1 ≤ pi ≤ n) — номера предков вершин с номерами от 2 до n. Вершина 1 является корнем дерева. Гарантируется, что значения pi определяют корректное дерево.
В каждой из последующих q строк записано одно целое число vi (1 ≤ vi ≤ n) — номер вершины, в поддереве которой надо найти центроид.
На каждый запрос выведите номер центроида соответствующего поддерева в отдельной строке. Если центроидов в поддереве несколько, выведите любой. Гарантируется, что у каждого поддерева заданного дерева есть хотя бы один центроид.
7 4
1 1 3 3 5 3
1
2
3
5
3
2
3
6
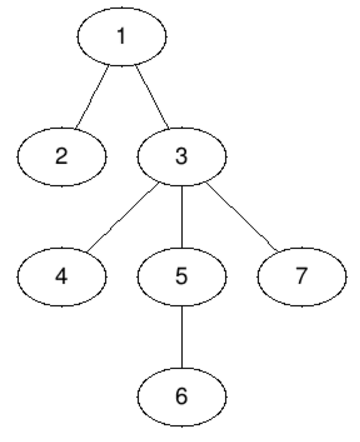
Первый вопрос спрашивает о центроиде всего дерева — это вершина 3, её удаление оставит четыре компоненты связности, две размера 1 и две размера 2.
Поддерево второй вершины состоит только из неё самой, поэтому ответ 2.
Вершина 3 также является центроидом собственного поддерева.
Центроидами поддерева 5 являются вершины 5 и 6 — оба этих ответа являются корректными.
| Название |
|---|




