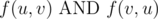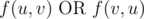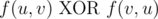| Good Bye 2017 |
|---|
| Закончено |
У вашего друга есть неизвестный вам ориентированный граф из n вершин.
Пусть f(u, v) будет истиной, если существует ориентированный путь из вершины u в вершину v, и ложью иначе. Для каждой пары различных вершин u, v вам известно, что как минимум одно из следующих утверждений верно:
Здесь AND, OR и XOR обозначают, соответственно, операции И, ИЛИ, исключающее ИЛИ.
Вам дана матрица n на n, показывающая, какое из этих утверждений верно для каждой пары вершин. Ячейка в u-й строке и v-м столбце содержит один символ.
- Если выполняется первое утверждение, то в ячейке находится 'A'.
- Если выполняется второе утверждение, то в ячейке находится 'O'.
- Если выполняется третье утверждение, то в ячейке находится 'X'.
- Ячейки на диагонали матрицы содержат только символы '-'.
Обратите внимание, возможно, некоторые пары вершин удовлетворяют сразу нескольким из утверждений, в таком случае, символ в матрице указывает на произвольное из выполняющихся утверждений для этой пары. Гарантируется, что матрица симметрична.
Вы хотите узнать, существует ли ориентированный граф, подходящий под данную матрицу. Если такого графа нет, выведите -1. Иначе выведите минимальное число ребер в графе, удовлетворяющем данным ограничениям.
Первая строка содержит одно целое число n (1 ≤ n ≤ 47) — количество вершин.
Следующие n строк содержат по n символов: матрицу с информацией о связности графа в формате, описанном выше.
Выведите минимальное число ребер в графе, удовлетворяющем условию, или -1, если такого графа не существует.
4
-AAA
A-AA
AA-A
AAA-
4
3
-XX
X-X
XX-
2
Пример 1: Данный граф является сильносвязным. Можно расположите все четыре вершины в один цикл.
Пример 2: Один из подходящих графов: 3 → 1 → 2. Для каждой пары различных вершин ровно одно из f(u, v), f(v, u) истинно.
| Название |
|---|