Привет! В прошлом посте я ввёл два вида динамического программирования: обычное и с симуляцией процесса. В нём я рассказал, как решать задачи на ДП, используя симуляцию процесса, пожалуйста, прочитайте, если пропустили, чтобы понимать разницу. Сейчас же я хочу поговорить о хитростях, которые помогают мне при решении задач на ДП обычным подходом.
Тогда как в симуляции процесса нам требовалось изобрести некий процесс, который бы строил нам необходимые объекты, в обычном подходе мы будем работать с объектами напрямую. Каждое состояние ДП (т. е., набор значений по каждому параметру) будет соответствовать некому классу желаемых объектов, а соответствующее значение в таблице ДП будет содержать информацию об этом классе, что в действительности эквивалентно формулировке через подзадачи, описанной в предыдущем посте.
Пример
informatics.msk.ru: Шаблон с ? и * Есть две строки, называемые "шаблонами", состоящие из латинских букв и знаков '*' и '?'. Строка считается подходящей под шаблон, если её можно получить из шаблона, заменив каждый '?' на некую букву и каждую '*' на некую последовательность букв (возможно пустую). Найдите длину кратчайшей строки, подходящей под оба шаблона.
Снова, если вы очень хотите, эту задачу можно решить и симуляцией процесса, но по-моему решение будет довольно неестественным. Так что продолжим с обычным подходом с подзадачами, а именно с подходом с классификацией объектов.
Давайте параметризуем эту задачу. Распространённым способом это сделать в таких задачах будет спросить тот же вопрос про некие два префикса шаблонов. То есть, "какая длина кратчайшей строки, подходящей под оба шаблона, но если мы рассматриваем толькоi символов первого и j символов второго шаблона?". Каждое состояние ДП будет соответствовать данному классу строк, а соответствующее значение в таблице ДП будет хранить длину кратчайшей такой строки.
Теперь предположим, что мы находим ответ для каждого такого вопроса в таком порядке, что когда мы обрабатываем состояние dp[i][j], мы уже знаем ответы для всех меньших пар префиксов (мы знаем все dp[i'][j'], гдеi' <= i и j' <= j кроме самой dp[i][j]). Как это знание поможет нам найти значение для текущего состояния? Ответ – мы должны рассмотреть текущую группу объектов и разделить её ещё на несколько видов. Рассмотрим три случая:
Если ни один из последних символов префиксов – не '*'. Тогда, очевидно, последний символ строки-ответа должен соответствовать обоим этим символам. Что означает, что если они являются двумя различными буквами, то множество ответов пусто (в этом случае мы храним inf, как длину кратчайшего ответа). В ином случае, без своего последнего символа строка-ответ подходит под префикс длины i - 1первого шаблона и под префикс длины j - 1 второго шаблона. Что означает, что существует взаимно-однозначное соответствие между множеством ответов для состояния dp[i][j] и множеством ответов для состояния dp[i - 1][j - 1]. И кратчайший ответ для dp[i][j] больше ответа дляdp[i - 1][j - 1] на один, т. е. dp[i][j] = dp[i - 1][j - 1] + 1.
Если оба последних символа префиксов – '*'. Тогда можно заметить, что среди всех ответов кратчайшим будет тот, где хотя бы одна из двух '*' соответствует в нём пустой строке (потому что иначе мы можем выкинуть несколько последних символов ответа и укоротить, оставив его валидным). Таким образом, мы можем разделить ответы/объекты, соответствующие состоянию dp[i][j] на три группы: те, где '*' из префикса первого шаблона заменяется на пустую строку, те, где '*' из префикса второго шаблона заменяется на пустую строку, и те, которые заведомо не кратчайшие. Мы знаем кратчайший ответ в первой группе (dp[i - 1][j]), мы знаем кратчайший ответ во второй группе (dp[i][j - 1]) и нам всё равно, что в третьей группе. Таким образом, в этом случаеdp[i][j] = min(dp[i - 1][j], dp[i][j - 1]).
Примечание: внимательный читатель мог заметить, что то, что мы считаем объектом в этой задаче – это в действительности не просто строка, соответствующая обоим шаблонам, а комбинация такой строки и такого соответствия (т. е., на какие конкретно символы были заменены '*', чтобы образовать эту строку).
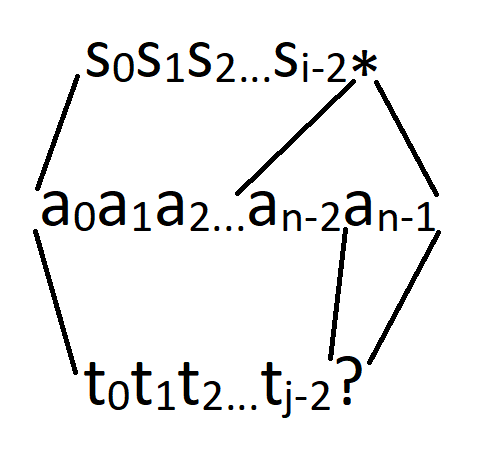
Если только один из последних символов префиксов – '*'. Это самый интересный случай, где не очевидно, как можно узнать ответ, зная ответ для меньших подзадач. В таких случаях я рекомендую забыть об остальном и спросить себя вновь, какие объекты нас интересуют? Предположим, что префикс первого шаблона – s[0]s[1]...s[i - 1], s[i - 1] == '*', а префикс второго шаблона – t[0]t[1]...t[j - 1], t[j - 1] != '*'. В этом случае, мы конкретно хотим найти строку a[0]a[1]...a[n - 1], такую, что a[n - 1] равно t[j - 1] (или любой букве, если t[j - 1] = '?') и a[0]a[1]...a[n - 2] подходит под префикс второго шаблона длиной j - 1, и с другой стороны какой-то её префикс – возможно вся строка – подходит под префикс перого шаблона длины i - 1.
Сначала разберитесь с очевидным
Первая часть условия – хорошая: "a[0]a[1]...a[n - 1] подходит под префикс втрого шаблона длины j - 1" означает, что мы можем обратиться к некому состоянию dp[...][j - 1], но что делать со второй частью? Мы можем сначала разобраться с очевидными случаями: когда '*' в первом шаблоне соответствует пустой строке в ответе – в этом случае длина кратчайшего такого ответа – это просто dp[i - 1][j].
Остаётся обработать лишь случай, когда '*' соответствует хотя бы одному символу, т. е. a[n - 1]. Но в таком случае a[0]a[1]...a[n - 2] подходит не только под префикс второго шаблона длины j - 1, но также и под префикс первого шаблона длины i, более того, существует взаимно-однозначное соответствие между объектами, которые нам осталось обработать, и объектами, соответствующими состоянию dp[i][j - 1]: каждая из требуемых строк может быть получена путём взятия некой строки, соответствующей dp[i][j - 1] и добавления к ней буквы t[j - 1] (или, допустим, буквы 'a', если t[j - 1] – это '?'). Это значит, что финальная формула в этом случае – это dp[i][j] = min(dp[i][j - 1], dp[i - 1][j] + 1).
Реализация
Базовые состояния ДП – те, где i = 0 или j = 0, в этом случаеdp[i][j] равно либо0, если все символы в префиксах – это '*', либо inf в остальных случаях. Сложность работы – очевидно, O(|s| * |t|).
Другой пример
607B - Zuma Дана последовательность чисел, вы можете удалить подряд-стоящий участок последовательности, если он является палиндромом. Найдите минимальное количество таких шагов, необходимых для удаление всей последовательности.
Глядя на ограничения, можно предположить, что параметры – это l и r, где dp[l][r] – это ответ для задачи, если бы существовал только полуинтервал последовательности с l включительно по r не включительно. Теперь надо подумать, как можно найти это значения, зная значения для всех вложенных полуинтервалов. Прежде всего, нужно определить, что в данном случае является объектом. Конечно, под объектом мы имеем в виду набор действий, ведущих к удалению всей строки. Иногда полезно визуально отобразить объект.
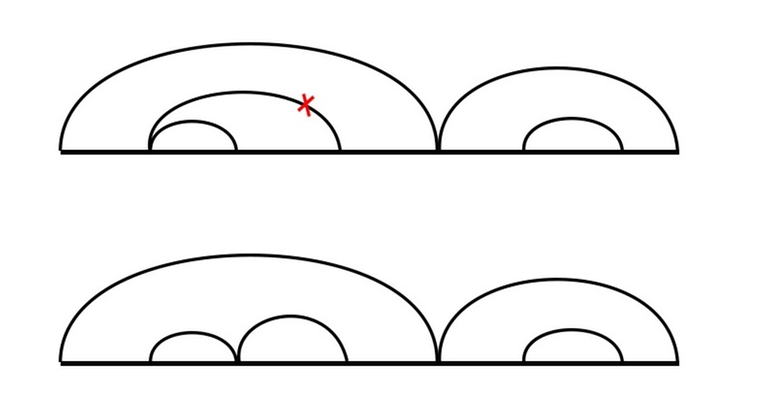
Давайте рисовать дугу над частями, которые удаляем. Дуга будет содержать другие дуги, соответствующие предыдущим удалениям вложенных частей. Давайте договоримся не рисовать дугу с l по r, если уже существует дугу с l по r' (r' < r), в этом случае мы могли бы просто нарисовать её от r' to r (так как остальное всё равно уже удалено). Аналогично будем поступать, если уже существует дуга сl' по r (l < l'). Таким образом, мы можем быть уверены, что крайний левый и крайний правый элементы под дугой удаляются тем непосредственно действием, соответствующий этой дуге.
Давайте последуем своему совету и сначала разберёмся с очевидными случаями. Для начала мы можем применить все переходы вида dp[l][r] = min(dp[l][r], dp[l][mid] + dp[mid][r]) (гдеl < mid < r), т. е. попробовать разделить интервал на два всеми возможными способами, и независимо удалить их оптимальным способом, к счастью, ограничения позволяют сделать это.
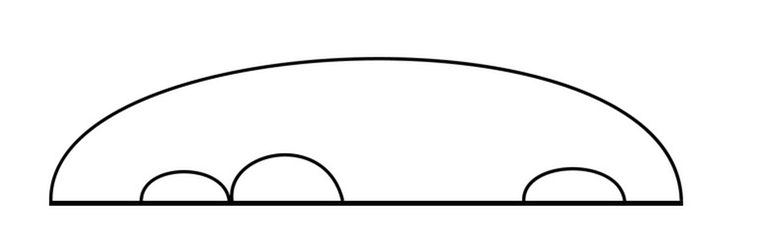
Объекты, непокрытые нами нельзя разделить на две независимые части – это те объекты, у которых дуга накрывает всю последовательность, или те, у которых крайний левый и крайний правый элементы удаляются на самом последнем шаге. Прежде всего, это предполагает, что крайний левый и крайний правый элементы равны, так как мы можем удалять только палиндромы. Если они не равны, то мы уже покрыли все случаи сделанными переходами. Иначе, всё ещё требуется найти кратчайший набор действий, который заканчивается одновременным удалением крайнего левого и крайнего правого элемента участка. Последнее действие фиксировано и не зависит от нас. Общий совет: если что-то не зависит от вас, попробуйте это учесть и затем абстрагироваться.
Давайте переформулируем, какие объекты мы ищем, но теперь без упоминания последнего действия: набор обговоренных действий на данном участке последовательности, которые не затрагивают крайний левый и крайний правый элементы и ведут к тому, что данный участок последовательности становится палиндромом (чтобы было возможно осуществить последнее действие: удалить весь участок). Другими словами, мы хотим знать, какое минимальное количество действий, чтобы сделать полуинтервал [l + 1, r - 1) палиндромом. Но это – конечно, dp[l + 1][r - 1] - 1, потому что каждый объект, соответствующий dp[l + 1][r - 1] – это по сути набор действий, приводящих к тому, чтобы этот участок стал палиндромом, а затем ещё одно действие, удаляющее его. Так что финальный переход, который нужно применить в случае, если c[l] = c[r - 1] – это dp[l][r] = min(dp[l][r], dp[l + 1][r - 1]) (сделать тот же самый набор действий, но в конце вместо удаления [l + 1, r - 1) удалить [l, r)).
Примечание: наша логика ломается, если r - l = 2, в этом случаеdp[l + 1][r - 1] = 0, так что мы не можем заменить последнее действие из набора. В этом случаеdp[l][r] = 1 (если c[l] = c[r - 1]).
Реализация
Базовое состояния ДП – это те, где r - l = 1, в этом случаеdp[l][r] равно 1. Сложность работы – O(n^3).
Заключении
Я надеюсь, что дал вам небольшое понимание, как легко придумать переходы в ДП с подзадачами. Если вам понравился пост, пожалуйста, поставьте лайк :)
Если хотите узнать больше, я напоминаю, что даю частные уроки по спортивному программированию, цена – $25/ч. Пишите мне в Telegram, Discord: rembocoder#3782, или в личные сообщения на CF.







