Здравствуйте. Это пролог к моим предыдущим постам, в котором я коротко введу читателя в терминологию динамического программирования. Это не исчерпывающий гайд, а лишь вступление, чтобы у неподготовленного читателя могла сложиться полная картина, какой её вижу я.
Базовые определения
Динамическое программирование – способ решения задачи путём её параметризации таким образом, чтобы ответ на задачу при одних значениях параметров помогал в нахождении ответа при других значениях параметров – а затем нахождения ответа при всех допустимых значениях параметров.
Состояние ДП – конкретный набор значений для каждого параметра (конкретная подзадача).
Значение ДП – ответ для конкретного состояния (подзадачи).
Переход из состояния A в состояние B – пометка, означающая, что для того, чтобы узнать значение для состояния B, требуется знать ответ для состояния A.
Реализовать переход из A в B – некое действие, проводимое, когда ответ для состояния A уже известен, удовлетворяющее условию: если реализовать все переходы, ведущие в B, то мы узнаем ответ для B. Само действие может отличаться от задачи к задаче.
Базовое состояние ДП – состояние, в которое нет переходов. Ответ для такого состояния ищется напрямую.
Граф ДП – граф, в котором каждая вершина соответствует состоянию, а каждое ребро – переходу.
Вычисление
Чтобы решить задачу, необходимо составить граф ДП – определиться, какие имеются переходы и как их реализовывать. Само собой, в графе ДП не должно быть циклов. Затем нужно найти ответ для всех базовых состояний и начать реализовывать переходы.
Мы можем реализовывать переходы в любом порядке, если выполняется следующее правило: не реализуйте переход из состояния A раньше перехода в состояние A. Но чаще всего используются два способа: с переходами назад и с переходами вперёд.
Реализация с переходами назад – проходим по всем вершинам в порядке топологической сортировки и для каждой фиксированной вершины реализуем все переходы в неё. Иными словами, на каждом шаге берём не посчитанное состояние и считаем для него ответ.
Реализация с переходами вперёд – проходим по всем вершинам в порядке топологической сортировки и для каждой фиксированной вершины реализуем все переходы из неё. Иными словами, на каждом шаге берём посчитанное состояние и реализуем переходы из него.
В разных случаях удобны разные способы реализации переходов, в том числе можно использовать и "кастомные".
Пример
В отличие от предыдущих постов, я не буду углубляться в то, как придумать решение, лишь продемонстрирую введённые понятия в действии.
AtCoder DP Contest: Задача K Два игрока по очереди достают из кучи камни, за один ход можно достать a[0], ..., a[n - 2] или a[n - 1] камней. Изначально в куче k камней. Кто выигрывает при оптимальное игре?
Параметром ДП будет i – сколько камней изначально находится в куче. Значением ДП будет 1, если в этой подзадаче выигрывает первый игрок, иначе – 0. Ответы будут храниться в массиве dp[i]. Зачастую само состояние i = x для краткости обозначается dp[x], я тоже буду пользоваться этим обозначением.
Назовём позицию выигрышной, если из неё побеждает тот, чей ход. Позиция выигрышная тогда и только тогда, когда из неё есть ход в проигрышную, т. е.dp[i] = 1 если для какого-то j (0 <= j < n, a[j] <= i) dp[i - a[j]] = 0, иначе dp[i] = 0.
Таким образом, будут существовать переходы из dp[i - a[j]] в dp[i] для всех i и j (a[j] <= i <= k, 0 <= j < n). Реализацией перехода в данном случае будет если dp[i - a[j]] = 0, присвоить dp[i] = 1. По умолчанию каждое состояние считается проигрышным (dp[i] = 0).
Базовым состоянием в данном случае будет dp[0] = 0. Граф динамики в случае k = 5, a = {2, 3}:
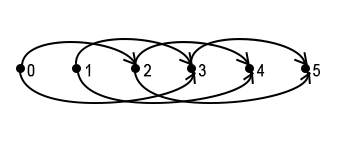
В этом коде я использую реализацию с переходами назад.
Другой пример
AtCoder DP Contest: Задача I Есть n монет, i-я монета падает решкой с вероятностью p[i]. Найти вероятность, что число решек будет больше числа орлов, если подбросить все монеты по одному разу.
Параметрами ДП будет i – сколько первых монет мы рассматриваем, и j – сколько должны выпасть решкой. Значением ДП будет вероятность, что ровно j упадут решкой, если подбросить первые i монет, оно будет храниться в массиве dp[i][j].
При i > 0 возможны два исхода, как могло выпасть j монет решкой: либо среди первых i - 1 выпадет решкой j - 1 и следующая тоже выпадет решкой: это возможно при j > 0, вероятность этого dp[i - 1][j - 1] * p[i - 1]; либо среди первых i - 1 выпадет решкой j, а следующая не выпадет решкой: это возможно при j < i, вероятность этого dp[i - 1][j] * (1 - p[i - 1]). dp[i][j] будет суммой этих двух вероятностей.
Таким образом, будут существовать переходы из dp[i][j] в dp[i + 1][j + 1] и в dp[i + 1][j] для всех i и j (0 <= i < n, 0 <= j <= i). Реализацией перехода из A в B в данном случае будет прибавить ответ для состояния A, помноженный на вероятность данного перехода, к ответу для состояния B. По умолчанию вероятность попасть в каждое состояние считается равным 0 (dp[i][j] = 0).
Это решение использует подход с симуляцией процесса, чтобы лучше его понять, читайте мой пост. Вкратце:
<spoiler summary="Мы симулируем процесс, где на каждом шаге подбрасывается одна монетка слева направо. dp[i][j] – суммарная вероятность всех путей, приводящих в данное состояние процесса. Изначально нам не известно ни одного пути, приводящего в какое-либо состояние, кроме как "пустого" пути в начальное состояние. Именно поэтому изначально все dp[i][j] равны 0, кроме dp[0][0], которое равно 1. При реализации перехода из A в B, мы обнаруживаем целый класс путей в состояние B, которые проходят через A, и прибавляем их суммарную вероятность к dp[B]."> ...
Базовым состоянием в данном случае будет dp[0][0] = 1. Граф динамики в случае n = 3:
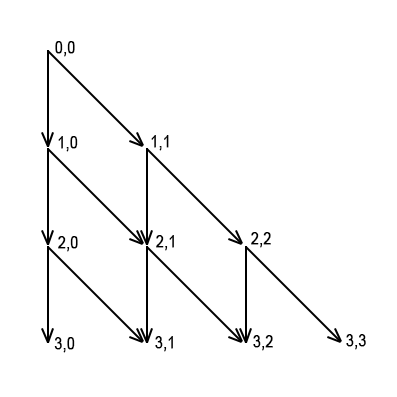
В этом коде я использую реализацию с переходами вперёд.
#include <bits/stdc++.h>
using namespace std;
#define int int64_t
int32_t main() {
ios_base::sync_with_stdio(0);
int n;
cin >> n;
vector<double> p(n);
for (int i = 0; i < n; i++) {
cin >> p[i];
}
vector<vector<double>> dp(n + 1, vector<double>(n + 1));
dp[0][0] = 1; // базовое состояние
for (int i = 0; i < n; i++) {
for (int j = 0; j <= i; j++) { // фиксируем состояние
dp[i + 1][j + 1] += dp[i][j] * p[i]; // реализуем
dp[i + 1][j] += dp[i][j] * (1 - p[i]); // переходы из него
}
}
double ans = 0;
for (int i = n / 2 + 1; i <= n; i++) {
ans += dp[n][i];
}
cout.precision(10);
cout << ans;
}
Заключение
После прочтения этой статьи я советую прочитать мои предыдущие два поста. В них я рассказываю про два вида динамического программирования, и это разделение мне кажется принципиальным для дальнейшего понимания.
Два вида динамического программирования: Симуляция процесса Как решать задачи на ДП: Обычный подход
Если хотите узнать больше, я напоминаю, что даю частные уроки по спортивному программированию, цена – $25/ч. Пишите мне в Telegram, Discord: rembocoder#3782, или в личные сообщения на CF.







