My first problem in 2023: "Genshin Geometry" !!!

#	User	Rating
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

#	User	Contrib.
1	cry	167
2	maomao90	163
2	Um_nik	163
4	atcoder_official	161
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	nor	153
9	Dominater069	153

Let your spirit soar and have a joy-filled new year by playing Ghenshin :D

However, before that, I will recommend you an interesting "Genshin Geometry" problem

(Problem F from the GYM The 2021 ICPC Asia Nanjing Regional Contest (XXII Open Cup, Grand Prix of Nanjing)).

Summary: Give N distint points on the plane, and special point O = (0, 0). Your task is dividing this N points into two sets A and B so that:

Both of them is a strict convex set.
The outlines(edge) of two convex hulls only intersect at point O.
The sum of the perimeters of these two convex hulls is maximum.

So now, let's try to solve this problem by yourself...

...before reading some hints!

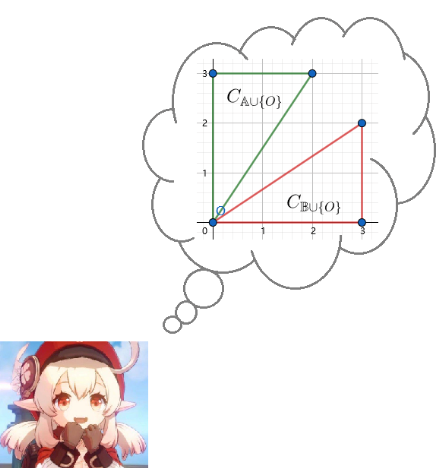
Firstly, let's answer this question: Is there any TRICKS to contruct these two sets optimally directly ?. (It becomes a Greedy problem!!!). In my opinion, this problem has a lot of cases, and the greedy solution is difficult to approach. So, I will representation a general solution, but if you have a more optimal solution, please leave your commend and everyone can reference.

Tags

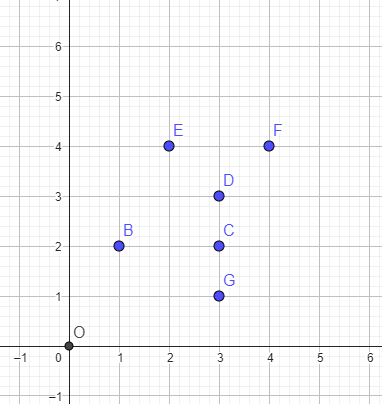
This problem has two general case. The first case is easier to approach: convex hull covers convex hull.

Image

So, set A is the convex hull of N points , and there are M remaining points that do not lie on this convex hull. Obviously, these M points are belong to the set B. Note, we need to check if remaining M points is strict convex and don't forget to the point O. Of course, finding convex hull is within O(NlogN)

But wait, is there any special cases?

The answer is

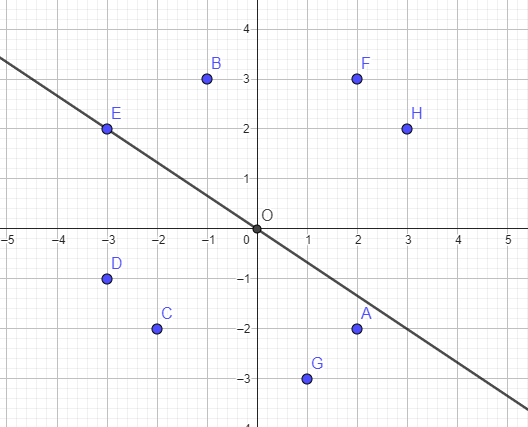
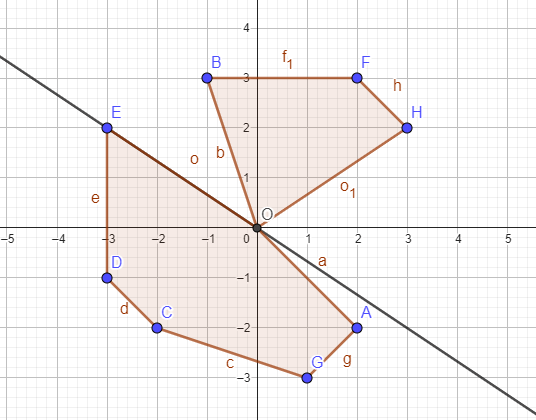
The second case is dividing line.

For example

The line connecting point O and any other point divides these N points into two groups. For more clearly, see this

Image

So, the solution is: For each point, divide N points with line connecting point O and that point into two groups, check if these groups are convex and find the maximum perimeters of all such dividing. But,

How to do it

Finnaly, below is my Accepted code for this problem. The first problem in 2023 with nearly 300 lines coding took me many hours. I think I should have a joy-filled by playing Ghenshin now :D. See you in the next Blog!

My solution

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
typedef long double ld;

struct point {
    int x, y, index;
    bool joined, isfault;
    point() {}
    point(int a, int b) {
        x = a, y = b;
    }
    bool operator < (point other) {
        return y < other.y || (y == other.y && x < other.x);
    }
    bool onSegment(point a, point b) {
        if (ccw(a, b) != 0) {
            return false;
        }
        int minx = min(a.x, b.x);
        int maxx = max(a.x, b.x);
        int miny = min(a.y, b.y);
        int maxy = max(a.y, b.y);
        return minx <= x && x <= maxx && miny <= y && y <= maxy;
    }
    int updown() {
        if (y < 0 || (y == 0 && x > 0)) {
            return 0;
        }
        return 1;
    }
    int ccw(point a, point b) {
        ll c = (ll)x * (a.y - b.y) + (ll)a.x * (b.y - y) + (ll)b.x * (y - a.y);
        if (c == 0) {
            return 0;
        }
        if (c > 0) {
            return 1;
        }
        return - 1;
    }
    ld dist(point other) {
        return hypot(x - other.x, y - other.y);
    }
};

point O = point(0, 0);

bool cmp(point a, point b) {
    if (a.updown() != b.updown()) {
        return a.updown() < b.updown();
    }
    return (ll)a.y * b.x < (ll)a.x * b.y;
}

vector <point> Build_ConvexHull(vector <point> &p) {
    vector <point> ans;
    sort(p.begin(), p.end());
    bool checking = true;
    for (int i = 0; i < p.size(); ++i) {
        if (p[0].ccw(p[1], p[i]) != 0) {
            checking = false;
            break;
        }
    }
    if (checking == true) {
        ans = p;
        p.clear();
        return ans;
    }

    for (int i = 0; i < p.size(); ++i) {
        p[i].index = i;
        p[i].joined = false;
    }
    vector <point> pts = p;
    int n = p.size(), sz = 0;
    p.resize(n + 1);
    for (int i = 1; i < n; ++i) {
        if (i == n - 1 || pts[0].ccw(pts[i], pts[n - 1]) >= 0) {
            while (sz > 0 && p[sz - 1].ccw(p[sz], pts[i]) < 0) {
                sz--;
            }
            p[++sz] = pts[i];
        }
    }
    if (sz != n - 1) {
        for (int i = n - 2, j = sz; i >= 0; --i) {
            if (i == 0 || pts[n - 1].ccw(pts[i], pts[0]) >= 0) {
                while (sz > j && p[sz - 1].ccw(p[sz], pts[i]) < 0) {
                    sz--;
                }
                p[++sz] = pts[i];
            }
        }
        p.resize(sz);
    }
    else {
        p.resize(sz + 1);
    }

    for (int i = 0; i < p.size(); ++i) {
        pts[p[i].index].joined = true;
    }
    ans = p;
    p.clear();
    for (auto i : pts) {
        if (i.joined == false) {
            p.push_back(i);
        }
    }

    return ans;
}

int main() {
    ios_base :: sync_with_stdio(false); cin.tie(0); cout.tie(0);
    if (fopen("test.inp", "r")) {
        freopen("test.inp", "r", stdin);
        freopen("test.out", "w", stdout);
    }

    int T;
    cin >> T;
    while (T--) {
        int n;
        cin >> n;
        vector <point> p(n);
        for (int i = 0; i < n; ++i) {
            cin >> p[i].x >> p[i].y;
        }
        vector <point> points = p;
        p.push_back(O);
        ld ans = 0;

        vector <vector <point>> pp(2);
        pp[0] = Build_ConvexHull(p);
        p.push_back(O);
        pp[1] = Build_ConvexHull(p);

        if (pp[0].size() + pp[1].size() == n + 2) {
            bool checking = true;
            for (int i = 0; i < 2; ++i) {
                if (pp[i].size() < 3) {
                    checking = false;
                    break;
                }
                bool contain = false;
                for (int j = 0; j < pp[i].size(); ++j) {
                    if (pp[i][j].x == 0 && pp[i][j].y == 0) {
                        contain = true;
                    }
                    int pre = (j - 1 + pp[i].size()) % pp[i].size();
                    int nxt = (j + 1) % pp[i].size();
                    if (pp[i][pre].ccw(pp[i][j], pp[i][nxt]) == 0) {
                        checking = false;
                        break;
                    }
                }
                if (contain == false) {
                    checking = false;
                }
                if (checking == false) {
                    break;
                }
            }
            if (checking == true) {
                for (int i = 0; i < 2; ++i) {
                    for (int j = 0; j < pp[i].size(); ++j) {
                        int nxt = (j + 1) % pp[i].size();
                        ans += pp[i][j].dist(pp[i][nxt]);
                    }
                }
            }
        }

        p = points;
        sort(p.begin(), p.end(), cmp);
        int pos = - 1;
        bool checking = true;
        for (int i = 0; i < n; ++i) {
            int nxt = (i + 1) % n;
            if (p[i].onSegment(O, p[nxt]) || p[nxt].onSegment(O, p[i])) {
                checking = false;
                break;
            }
        }
        if (checking == true) {
            for (int i = 0; i < n; ++i) {
                int pre = (i - 1 + n) % n;
                int nxt = (i + 1) % n;
                if (p[pre].ccw(p[i], p[nxt]) < 0 || p[i].onSegment(p[pre], p[nxt])) {
                    p[i].isfault = true;
                }
                else {
                    p[i].isfault = false;
                }
                p[i].index = i;
            }

            vector <deque <point>> pts(2);
            vector <ld> len(2, 0);
            vector <int> fault(2);
            vector <bool> status(2, true);
            pts[0].push_back(p[0]);
            for (int i = 1; i < n; ++i) {
                if (p[0].ccw(O, p[i]) < 0) {
                    len[0] += pts[0].back().dist(p[i]);
                    if (pts[0].size() >= 2 && pts[0].back().isfault == true) {
                        status[0] = false;
                        fault[0] = pts[0].back().index;
                    }
                    pts[0].push_back(p[i]);
                }
                else {
                    if (pts[1].size()) {
                        len[1] += pts[1].back().dist(p[i]);
                    }
                    if (pts[1].size() >= 2 && pts[1].back().isfault == true) {
                        status[1] = false;
                        fault[1] = pts[1].back().index;
                    }
                    pts[1].push_back(p[i]);
                }
            }
            if ((status[0] && pts[0].size() >= 2 && O.ccw(pts[0].front(), pts[0].back()) > 0)
                && (status[1] && pts[1].size() >= 2 && O.ccw(pts[1].front(), pts[1].back()) > 0)) {
                ans = max(ans, len[0] + O.dist(pts[0].front()) + O.dist(pts[0].back()) + len[1] + O.dist(pts[1].front()) + O.dist(pts[1].back()));
            }

            for (int i = 1; i < n; ++i) {
                point curr = pts[0].front();
                if (pts[1].size()) {
                    len[1] += pts[1].back().dist(curr);
                }
                if (pts[1].size() >= 2 && pts[1].back().isfault == true) {
                    status[1] = false;
                    fault[1] = pts[1].back().index;
                }
                pts[1].push_back(curr);
                pts[0].pop_front();
                if (pts[0].size()) {
                    len[0] -= pts[0].front().dist(curr);
                    if (status[0] == false) {
                        if (pts[0].front().isfault == true && pts[0].front().index == fault[0]) {
                            status[0] = true;
                        }
                    }
                }
                else {
                    pts[0].push_back(p[i]);
                    point curr = pts[1].front();
                    pts[1].pop_front();
                    if (pts[1].size()) {
                        len[1] -= pts[1].front().dist(curr);
                        if (status[1] == false) {
                            if (pts[1].front().isfault && pts[1].front().index == fault[1]) {
                                status[1] = true;
                            }
                        }
                    }
                }

                while (pts[1].size() > 0 && p[i].ccw(O, pts[1].front()) < 0) {
                    curr = pts[1].front();
                    len[0] += pts[0].back().dist(curr);
                    if (pts[0].size() >= 2 && pts[0].back().isfault == true) {
                        status[0] = false;
                        fault[0] = pts[0].back().index;
                    }
                    pts[0].push_back(curr);
                    pts[1].pop_front();
                    if (pts[1].size()) {
                        len[1] -= pts[1].front().dist(curr);
                        if (status[1] == false) {
                            if (pts[1].front().isfault == true && pts[1].front().index == fault[1]) {
                                status[1] = true;
                            }
                        }
                    }
                }

                if ((status[0] && pts[0].size() >= 2 && O.ccw(pts[0].front(), pts[0].back()) > 0)
                    && (status[1] && pts[1].size() >= 2 && O.ccw(pts[1].front(), pts[1].back()) > 0)) {
                    ans = max(ans, len[0] + O.dist(pts[0].front()) + O.dist(pts[0].back()) + len[1] + O.dist(pts[1].front()) + O.dist(pts[1].back()));
                }
            }
        }

        cout << fixed << setprecision(10) << ans << "\n";
    }
}

Rev.	By	When	Δ	Comment
en61	Yunannnn	2023-01-02 17:30:31	0	(published)
en60	Yunannnn	2023-01-02 17:29:27	8	Tiny change: ' return — 1;\n }' -> ' return - 1;\n }'
en59	Yunannnn	2023-01-02 17:28:04	64
en58	Yunannnn	2023-01-02 17:22:47	5
en57	Yunannnn	2023-01-02 17:20:54	452
en56	Yunannnn	2023-01-02 17:11:12	21
en55	Yunannnn	2023-01-02 17:10:04	440
en54	Yunannnn	2023-01-02 16:58:51	106
en53	Yunannnn	2023-01-02 16:55:07	249
en52	Yunannnn	2023-01-02 16:47:19	54
en51	Yunannnn	2023-01-02 16:46:19	3	Tiny change: ' N is 10^6.\n</spoil' -> ' N is $10^6$.\n</spoil'
en50	Yunannnn	2023-01-02 16:45:11	320
en49	Yunannnn	2023-01-02 16:38:11	53
en48	Yunannnn	2023-01-02 16:34:18	197
en47	Yunannnn	2023-01-02 16:27:25	40
en46	Yunannnn	2023-01-02 16:25:15	7	Tiny change: '(https://imgur.com/vj1L69y)\n</spoil' -> '(https://i.imgur.com/vj1L69y.png)\n</spoil'
en45	Yunannnn	2023-01-02 16:24:27	15	Tiny change: 'j1L69y)\n<spoiler' -> 'j1L69y)\n</spoiler>\n\n<spoiler'
en44	Yunannnn	2023-01-02 16:23:32	151
en43	Yunannnn	2023-01-02 16:18:04	1453
en42	Yunannnn	2023-01-02 16:14:21	9703
en41	Yunannnn	2023-01-02 16:12:02	3	Tiny change: 'so easy.\n![ ](htt' -> 'so easy.\n\n![ ](htt'
en40	Yunannnn	2023-01-02 16:11:24	160
en39	Yunannnn	2023-01-02 16:01:17	43	Tiny change: 'O_. :D\n\n[My so' -> 'O_. :D\n\nBut wait, is there any special cases?\n\n\n[My so'
en38	Yunannnn	2023-01-02 15:58:41	22
en37	Yunannnn	2023-01-02 15:57:49	262
en36	Yunannnn	2023-01-02 15:51:00	40
en35	Yunannnn	2023-01-02 15:49:41	17	Tiny change: 'x hull. \n\n ![ ](https' -> 'x hull. \n![ ](https'
en34	Yunannnn	2023-01-02 15:49:27	33	Tiny change: ' ' -> ' '
en33	Yunannnn	2023-01-02 15:49:11	48
en32	Yunannnn	2023-01-02 15:48:44	82
en31	Yunannnn	2023-01-02 15:48:20	37	Tiny change: 'Let your s' -> '![ ](https://i.imgur.com/YeyVfBl.png)Let your s'
en30	Yunannnn	2023-01-02 15:40:31	41
en29	Yunannnn	2023-01-02 15:37:15	348
en28	Yunannnn	2023-01-02 15:35:12	350
en27	Yunannnn	2023-01-02 15:33:39	62
en26	Yunannnn	2023-01-02 15:32:31	69
en25	Yunannnn	2023-01-02 15:30:30	1	Tiny change: 'hull. \n\n[](/predow' -> 'hull. \n\n![](/predow'
en24	Yunannnn	2023-01-02 15:29:09	68	Tiny change: 'ull. \n\n[](https://' -> 'ull. \n\n[Your text to link here...](https://'
en23	Yunannnn	2023-01-02 15:15:16	2	Tiny change: 'hull. \n\n(https://c' -> 'hull. \n\n[](https://c'
en22	Yunannnn	2023-01-02 15:14:48	74	Tiny change: 'hull. \n\n\n\n[My so' -> 'hull. \n\nhttps://mirror.codeforces.com/b373d7/3.png\n\n[My so'
en21	Yunannnn	2023-01-02 15:14:23	65	Tiny change: 'hull. \n\n\n\n[My so' -> 'hull. \n\nhttps://mirror.codeforces.com/b373d7/3.png\n\n[My so'
en20	Yunannnn	2023-01-02 15:10:51	109
en19	Yunannnn	2023-01-02 15:07:14	241
en18	Yunannnn	2023-01-02 15:05:47	2	Tiny change: 'n(Problem from the ' -> 'n(Problem F from the '
en17	Yunannnn	2023-01-02 15:05:19	388
en16	Yunannnn	2023-01-02 14:53:17	243
en15	Yunannnn	2023-01-02 14:45:49	121
en14	Yunannnn	2023-01-02 14:41:43	98
en13	Yunannnn	2023-01-02 14:40:15	757
en12	Yunannnn	2023-01-02 14:38:45	57
en11	Yunannnn	2023-01-02 14:37:05	3	Tiny change: 'ALw_wcB#/). \n\nHoweve' -> 'ALw_wcB#/) :D\n\nHoweve'
en10	Yunannnn	2023-01-02 14:35:58	4	Tiny change: 'w_wcB#/). However, b' -> 'w_wcB#/). \n\nHowever, b'
en9	Yunannnn	2023-01-02 14:35:37	137
en8	Yunannnn	2023-01-02 14:31:59	63
en7	Yunannnn	2023-01-02 14:29:54	267
en6	Yunannnn	2023-01-02 14:25:46	2	Tiny change: '03470]\n\n<spoil' -> '03470]\n\n\n<spoil'
en5	Yunannnn	2023-01-02 14:23:29	23
en4	Yunannnn	2023-01-02 14:21:36	52
en3	Yunannnn	2023-01-02 14:19:25	45	Tiny change: '03470]\n\n[My so' -> '03470]\n\n<spoiler summary="Tags">\naaa\n</spoiler>\n\n[My so'
en2	Yunannnn	2023-01-02 14:17:49	112
en1	Yunannnn	2023-01-02 14:13:47	64	Initial revision (saved to drafts)

History