Ever since I read this blog, I have been curious to see how other space-filling curves other than Hilbert can be used to reduce the run time. In this blog, we will see how Peano curves can help bring down the run time of Mo's algorithm-based solutions.

Prerequisites: Mo's algorithm, Mo's algorithm using Hilbert Curve order

Relation to TSP

In Mo's algorithm, we try to come up with a comparator that can help us sort the queries in such a way that minimizes the total movement of L and R pointers. In other words, if we have $$$Q$$$ queries, each of the form $$$l_i$$$, $$$r_i$$$, then we wish to find such an arrangement of the queries that minimizes the following summation:

$$$S = \displaystyle\sum_{i=1}^{Q-1} |l_i - l_{i+1}| + |r_i - r_{i+1}|$$$.

Each query $$$(l,r)$$$ can be viewed as a coordinate on a 2D plane. We want to visit each of these points such that the travelled distance (with Manhattan distance as the distance metric) is minimized. This problem is the same as Traveling Salesman Problem (TSP), but a variant in which the salesman does not need to return to the starting city / point.

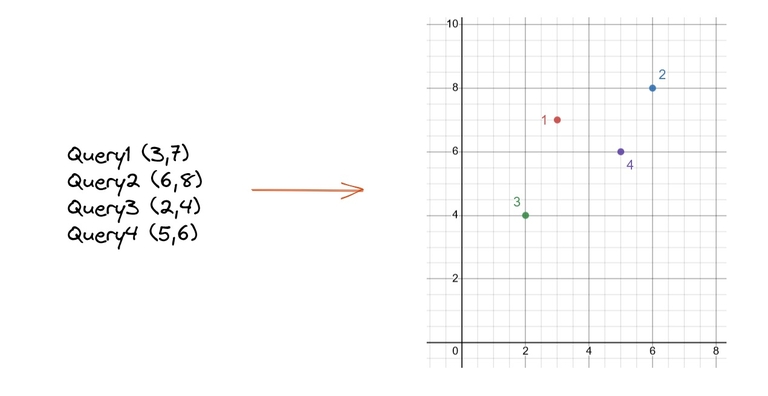
This problem is NP-Hard, taking exponential time to find the best minimum cost. However, we can trade-off time with accuracy. We can find a good enough solution which takes polynomial time and is fast enough. This is what space-filling curve based heuristic solutions help us achieve. Since the summation minimization problem is the same as TSP, we can apply the same heuristic approaches to Mo's algorithm. Let's try to find a new comparator based on all this information.

New Comparator

A comparator that uses Hilbert curve order has already been explained in this blog quite nicely. Here I will discuss a comparator that uses Peano curve order.

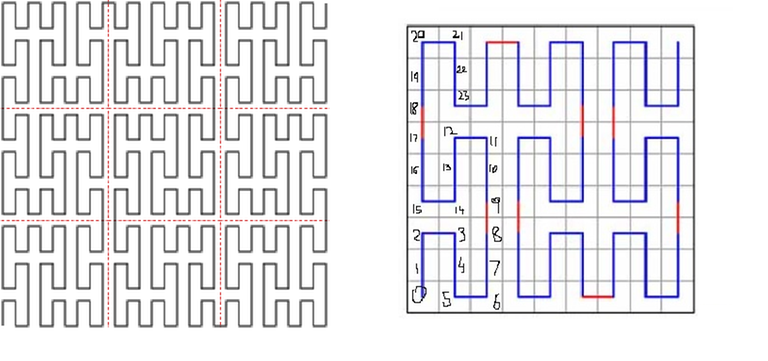
Let's build a Peano curve on a $$$3^k × 3^k$$$ matrix and visit all the cells on the matrix according to this curve. Denote ord(i, j, k) as the number of cells visited before the cell (i, j) in order of Peano curve on the $$$3^k × 3^k$$$ matrix. We sort the queries in non-descending order w.r.t. their value of ord(i,j,k).

Butz gives an algorithm for computing the Peano space-filling curve in terms of the base-3 representation of coordinates. It generalizes pretty well with higher dimensions. I will describe the algorithm briefly, assuming a point in an n-dimensional plane.

1. List down the coordinates in base 3 representation. Each coordinate takes up k places in the base 3 / ternary representation. Here, we choose k such that k satisfies $$$3^k \geq N$$$ (N is the maximum value a coordinate can take).
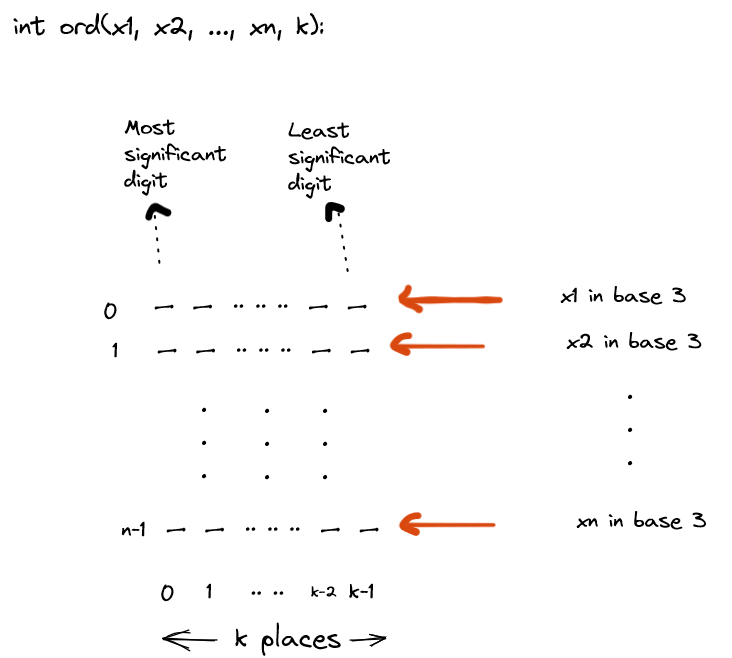
   Each row is a coordinate, taking up k places to write in ternary form. Let this matrix formed be denoted by $$$a$$$
   
   

2. Perform $$$\text{peano-flip}$$$ on each $$$a_{i,j}$$$. It is a function that modifies $$$a_{i,j}$$$ values.
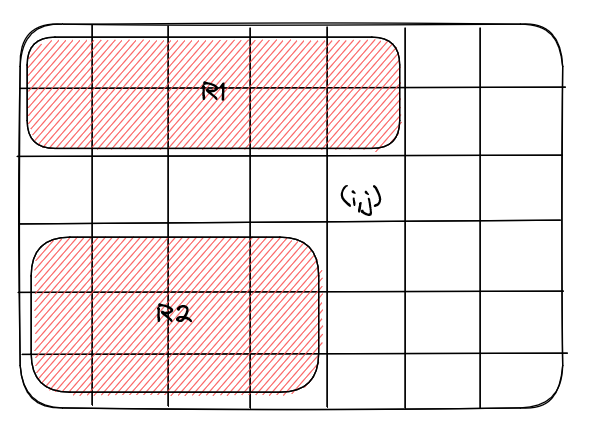
   $$$R2$$$ corresponds to the sum of values in columns left of column $$$j$$$ which are not in row $$$i$$$
   $$$R1$$$ corresponds to the sum of values in column $$$j$$$ above row $$$i$$$
   If $$$R1 + R2$$$ is odd, do: $$$a_{i,j} = 2 - a_{i,j}$$$
   Else we do nothing.
   
   

3. Let ord(i,j,k) = num. Then, num is obtained by constructing a number off $$$a_{i,j}$$$ in base 10 in the following way:

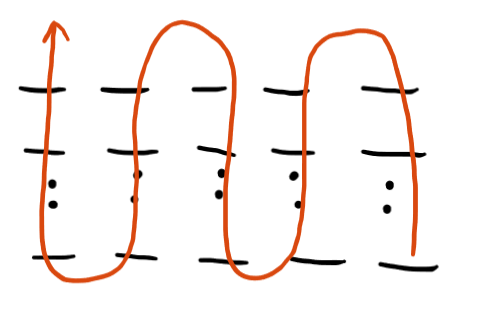
For example, let's find Peano order for the query (3, 8). We can choose k = 2 as $$$3^2 \geq 8$$$.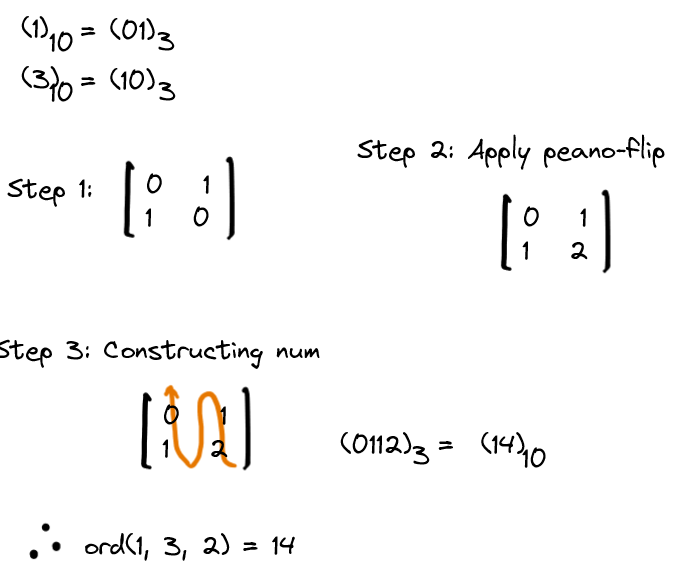
You can verify from the peano order diagram that (1, 3) corresponds to 14 (assuming 0 based indexing).

Here is an implementation of Peano order for our 2 dimensional queries:

inline int64_t peanoOrder(int x,int y,int m) {
    vector<vector<int>> a(2, vector<int>(m));
    int sum0 = 0, sum1 = 0;
    int ptr = m-1;
    while (x) {
        a[0][ptr] = x%3;
        sum0 += a[0][ptr];
        ptr--;
        x /= 3;
    }
    ptr = m-1;
    while (y) {
        a[1][ptr] = y%3;
        sum1 += a[1][ptr];
        ptr--;
        y /= 3;
    }

    for (int i = m-1; i >= 0; i--) {
        sum1 -= a[1][i];
        if (sum0&1)
            a[1][i] = 2 - a[1][i];
        sum0 -= a[0][i];
        if (sum1&1)
            a[0][i] = 2 - a[0][i];
    }

    int64_t num = 0, base = 1;
    for (int j = m-1; j >= 0; j--) {
        num += base * a[1][j];
        base *= 3;
        num += base * a[0][j];
        base *= 3;
    }
    return num;
}

We can take k = 13 for all practical reasons, as $$$3^{13} \geq 10^{6}$$$

Use in problems

But how does Peano order compare with Hilbert order and the canonical version?