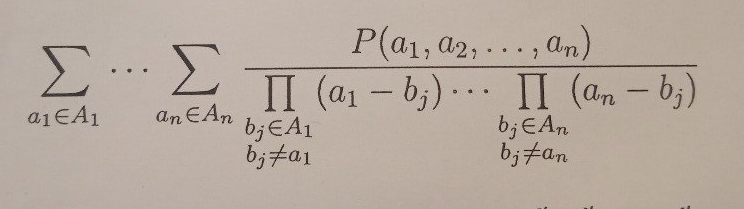Hello, Codeforces. I wrote a prorgam using this theorem for interpolation a function as a polynomial. At first, I will explain how does it work and then show some examples of using it.
Wikipedia does not provide one formula I need, so I will show it
Code is quite long, but simple in use.
How to use program
At first, you need to set values of constants. N is the number of variables, MAX_DEG is the maximal exponent of a variable over all monomials. In main you need to fill 2 arrays: names contains the names of all variables, max_exp[i] is the maximal exponent of the i-th variable, or the upper_bound of its value.
Define d = (max_exp[0] + 1) * (max_exp[1] + 1) * ... * (max_exp[N - 1] + 1). MAX_PRODUCT should be greater then d. Then you need to write a function f(array<ll, N>), which returns ll or ld. In my code it returns an integer, but its type is ld to avoid ll overflow.
Stress-testing
If you uncomment 2 last rows in main, program will check the polynom it got on random tests. The test generation should depend from f working time, because it can run too long on big tests.
Approximations
Function from exaple and similar functions (with n loops) are a polynomial with rational coefficients (if this is not true, the function does not return an integer). So, if APPROXIMATION = true, all coefficients are approximating to rational numbers with absolute error < EPS with functions normalize and approximate (they are using the same algorithm). This algorithm works in O(numerator + denominator), that seems to be slow, but if the polynomial has a small amount of monomials, it does not take much time.
Stress-testing function check considers a value correct if its absolute or relative error < EPS_CHECK.
How and how long does it work
We consider monomials as arrays of exponents. We hash these arrays. Array PW contains powers of points (from POINTS), which we use for interpolation. If you want to use your points for interpolation, modify POINTS. If you use fractional numbers, replace #define ll long long with #define ll long double. Array DIV is used for fast calculating denominators in the formula.
convert(h) — get indexes (in array POINTS) of coordinates of the point corresponding to the monomial with hash h. convert_points(h) — get coordinates of the point corresponding to the monomial with hash h.
Then we are precalcing values of f in all our points and write them to F_CACHE. After it, we run bfs on monomials. During the transition from one monomial to another we decrease the exponent of one variable by 1. When a monomial is got from set in bfs, we find its coefficient using gen. If it is not zero, we need to modify our polynomial for every monomials we has not considered in bfs yet ("monomial" and "point" have the same concepts because we can get a point from monomial using convert_points(h), if h is a hash of the monomial).
We need to modify the polynomial to make one of the theorem's conditions satisfied: there are no monomials greater than our monomial (greater means that all exponents are more or equal). For every point we has not consider in bfs (they will be in set remaining_points) we add the value of the monomial in this point to SUM[hash_of_point]. Then we will decrease f(point) by SUM[hash_of_point] to artificially remove greater monomials.
Time complexity
- The longest part of precalc — calculating F_CACHE — take O(d * O(f)) time
- Each of d runs of
genis iterating over O(d) points, denominator calculation takes O(N) time for each point. - For every monomial with non-zero coefficient we calculate its values in O(d) points in O(N) for each point.
We have got O(d * O(f) + d^2 * N + d * O(res)), where O(res) is the time it takes to calculate the polynomial we got as a result.
Trying to optimize
It seems that the recursion takes the most time. We can unroll it in one cycle using stack. It is boring, so I decided to try to unroll it in other way. For every monomial with non-zero coefficient, let`s iterate over all monomials with hash less or equal to our hash. For every monomial we check if it is less than our monomial (all corresponding exponents are less or equal). If it is lower, we add to the coefficient the value of fraction in this point (monomial).
// Instead of ld k = gen();
ld k = 0;
for (int h=0;h<=v;h++)
{
array<int, N> cur = convert(h);
bool ok = 1;
for (int i=0;i<N;i++) if (cur[i] > cur_exp[i]) ok = 0;
if (ok)
{
ll div = 1;
for (int i=0;i<N;i++) div *= DIV[i][cur[i]][cur_exp[i]];
k += (ld)(F_CACHE[h] - SUM[h]) / div;
}
}Is it faster than gen? New implementation is iterating over all pairs of hashes, so it works in O(d^2 * N), too. Let's estimate the constant. The number of these pairs is d * (d + 1) / 2, so we get constant 1 / 2. Now let's calculate the constant of number of points considered by gen. This number can be calculated with this function:
ld f(array<ll, N> v)
{
auto [a, b, c, d, e, f, g] = v;
ld res = 0;
for (int i=0;i<a;i++)
for (int j=0;j<b;j++)
for (int u=0;u<c;u++)
for (int x=0;x<d;x++)
for (int y=0;y<e;y++)
for (int z=0;z<f;z++)
for (int k=0;k<g;k++)
res += (i + 1) * (j + 1) * (u + 1) * (x + 1) * (y + 1) * (z + 1) * (k + 1);
return res;
}The coefficient with a^2 * b^2 * c^2 * d^2 * e^2 * f^2 is our constant. To find it, I used my program. It is 1 / 128. At all, it is 1 / 2^N for N variables. It means that the optimization can be efficient if N is small.
Conclusion
May be, this program will help someone to find formula for some function. Also it can open brackets, that is necessary if you calculate geometry problems in complex numbers. If you know other ways to use it, I will be happy if you share it.
With N = 1 this program is just a Lagrange interpolation, which can be done faster than O(d^2). Maybe, someone will find a way to speed up it with N > 1.