Segment Tree is a powerful data structure in programming, that is why it can still be optimized way more. In this blog I will explain one optimization that can make a basic segment tree slightly faster and easier to write.
This does not work on range update range query segment trees.
Prerequisites:
- basic/intermediate segment tree skills
- good bitwise operations knowledge
Introduction:
lets consider a point update range query segment tree, while querying we visit many of useless Nodes along the way in order to answer the query moving from the root downwards.
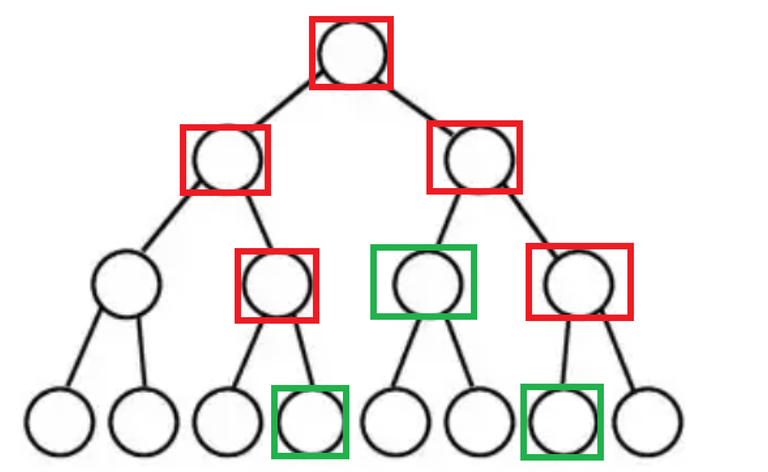
As you can see, there are nodes (marked in red) that are not needed during the recursion, and we only need to visit the important nodes (marked in green).
This is only true when querying in a point update segment tree or updating in a range query segment tree.
Main Idea:
we can solve a query range $$$[l, r]$$$ by noticing we can make it a smaller range $$$[l + X , r]$$$ where X is any power of two but we need it to be maximum and $$$l + X - 1 <= r$$$ and a $$$[l, l + X - 1]$$$ is a valid node in the segment tree.
at the end we can solve it now because $$$X$$$ is $$$2$$$ power the minimum between $$$log_2(r-l+1)$$$ and $$$log_2(M & -M)$$$ .
C++ Code:
we can preprocess $$$log_2(K)$$$ for each $$$1 <= K <= N$$$ in an array.
note that this only works when $$$N$$$ (the number of leaves) is a power of 2.
at each step we calculate the size of the movement $$$X$$$
The following codes calculate sum in the range $$$L$$$ to $$$R$$$, assuming the segment tree is built after possibly several updates.
Recursive:
long long query(int l, int r){
if(l > r)return 0;
int node = N + l - 1;
int X = min(logs[node & -node], logs[r-l+1]);
return (query(l + (1<<X), r) + seg[node >> moves]);
}
Iterative:
long long query(int l, int r){
long long ret = 0;
while(l<=r){
int node = N + l - 1;
int X = min(logs[node & -node], logs[r - l + 1]);
ret = (ret + seg[node >> X]);
l += (1 << X);
}
return ret;
}
This can also be applied to range update point query segment trees:
void update(int l, int r, int k){
while(l<=r){
int node = x + l - 1;
int X = moves = min(logs[node & -node], logs[r - l + 1]);
seg[node >> moves] += k;
lazy[node >> moves] = 1;
l += (1 << moves);
}
}





