GCD

• Gcd of two natural number $$$a$$$ and $$$b$$$ is defined as the largest number which is a divisor of both $$$a$$$ and $$$b$$$.

• Mathematically it is defined as: GCD(a, b)= max{k>0: (k/a) and (k/b)}.(Here $$$k$$$/$$$a$$$ means $$$k$$$ divides  $$$a$$$).

  Ways to find GCD

  Brute Force

• We can find gcd of two number by checking for all integer less than both number.

• We never use this approach to find gcd because this run in O(n) time complexity.

  Euclidean algorithm

• The Euclidean algorithm was formulated as follows: subtract the smaller number from the larger one until one of the numbers is zero. Indeed, if   $$$g$$$ divides   $$$a$$$ and   $$$b$$$, it also divides   $$$a-b$$$. On the other hand, if   $$$g$$$ divides   $$$a-b$$$ and   $$$b$$$, then it also divides   $$$a = b + (a-b)$$$, which means that the sets of the common divisors of   $$${a, b}$$$ and   $$${b,a-b}$$$ coincide.

• $$$a$$$ remains the larger number until   $$$b$$$ is subtracted from it at least   $$$\left\lfloor\frac{a}{b}\right\rfloor$$$ times. Therefore, to speed things up,   $$$a-b$$$ is substituted with $$$a-\left\lfloor\frac{a}{b}\right\rfloor b = a \bmod b$$$.

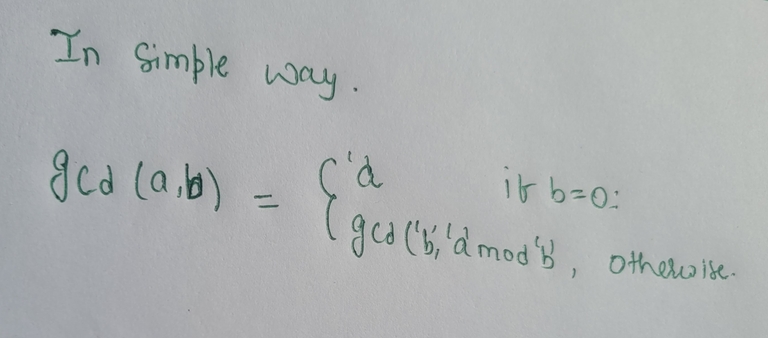
Implementation Using Code

1. Recursive Code

    int gcd (int a, int b) {
       if (b == 0)
        return a;
       else
     return gcd (b, a % b);
     }

This code run in O(log min(a, b)) Time complexity and in Recursive Stack space complexity.

2. Iterative Solution

    int gcd (int a, int b) {
      while (b) {
        a %= b;
        swap(a, b);
      }
      return a;
    }

This code run in O(log min(a, b)) Time complexity and But it take a constant space complexity as we have only define two variable only. This solution is is more faster than recursive one because of recursive call take more time than normal iteration.

Binary GCD

Above method works in time complexity of O(log n).we can more optimize this as we all know that The slow part of the normal algorithm are the modulo operations. Modulo operations, although we see them as   $$$O(1)$$$, are a lot slower than simpler operations like addition, subtraction or bitwise operations.. Here comes the Binary GCD in role.

This uses three very popular properties of GCD

• If both numbers are even, then we can factor out a two of both and compute the GCD of the remaining numbers:   $$$\gcd(2a, 2b) = 2 \gcd(a, b)$$$.
• If one of the numbers is even and the other one is odd, then we can remove the factor 2 from the even one:   $$$\gcd(2a, b) = \gcd(a, b)$$$ if   $$$b$$$ is odd.
• If both numbers are odd, then subtracting one number of the other one will not change the GCD:   $$$\gcd(a, b) = \gcd(b, a-b)$$$

Implementation Using Code

    int gcd(int a, int b) {
      if (!a || !b)
        return a | b;
      unsigned shift = __builtin_ctz(a | b);
      a >>= __builtin_ctz(a);
      do {
        b >>= __builtin_ctz(b);
        if (a > b)
            swap(a, b);
        b -= a;
      } while (b);
     return a << shift;
    }

Thanks.