Всем привет!
Надеемся, что вам понравились наши задачи!
Спасибо за участие!
Автор: ooaa
Устойчивость стены — это число горизонтальных кирпичей минус число вертикальных. Так как горизонтальный кирпич длины хотя бы $$$2$$$, в одном ряду можно разместить не более $$$\lfloor\frac{m}{2}\rfloor$$$ горизонтальных кирпичей. Поэтому ответ не превосходит $$$n \cdot \lfloor\frac{m}{2}\rfloor$$$. С другой стороны, если размещать в ряду горизонтальные кирпичи длины $$$2$$$, и, когда $$$m$$$ нечётно, последний кирпич длины $$$3$$$, то в каждом ряду будет ровно $$$\lfloor\frac{m}{2}\rfloor$$$ горизонтальных кирпичей, и вертикальных кирпичей в стене вообще не будет. Так достигается максимальная устойчивость $$$n \cdot \lfloor\frac{m}{2}\rfloor$$$. Решение — это одна формула, асимптотика $$$O(1)$$$.
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--)
{
int64_t n,m;
cin >> n >> m;
cout << n*(m/2) << '\n';
}
return 0;
}
1918B — Минимизируйте инверсии
Автор: ace5
Заметим, что операциями вида: поменять местами $$$a_i$$$ с $$$a_j$$$ и $$$b_i$$$ с $$$b_j$$$ одновременно можно переставить массив $$$a$$$ как угодно, но одному и тому же $$$a_i$$$ будет соответствовать одно и то же $$$b_i$$$ (потому что меняем и $$$a_i$$$ и $$$b_i$$$ сразу). Давайте отсортируем такими операциями массив $$$a$$$. Тогда суммой количества инверсий в $$$a$$$ и $$$b$$$ будет количество инверсий в $$$b$$$, так как $$$a$$$ отсортирован. Утверждается, что это минимальная сумма, которую можно достичь.
Доказательство: Рассмотрим две пары элементов $$$a_i$$$ с $$$a_j$$$ и $$$b_i$$$ с $$$b_j$$$ ($$$i$$$ < $$$j$$$). В каждой из этих пар может быть либо $$$0$$$, либо $$$1$$$ инверсия, то есть среди двух пар либо $$$0$$$, либо $$$1$$$, либо $$$2$$$ инверсии. Если до операции было $$$0$$$ инверсий, то после операции станет две, если была $$$1$$$, то и останется $$$1$$$, если было $$$2$$$, то станет $$$0$$$. Если перестановка $$$a_i$$$ отсортирована, то в каждой паре индексов $$$i$$$ и $$$j$$$ будет максимум $$$1$$$ инверсия, поэтому любая пара индексов будет давать не больше инверсий, чем если их поменять. Поскольку в каждой паре количество инверсий минимально возможное, то и общее количество инверсий минимально возможное.
Асимптотика: $$$O(n)$$$ на набор входных данных.
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
pair<int,int> ab[n];
for(int i = 0;i < n;++i)
{
cin >> ab[i].first;
}
for(int i = 0;i < n;++i)
{
cin >> ab[i].second;
}
sort(ab,ab+n);
for(int i = 0;i < n;++i)
{
cout << ab[i].first << ' ';
}
cout << "\n";
for(int i = 0;i < n;++i)
{
cout << ab[i].second << ' ';
}
cout << "\n";
}
}
Автор: ace5
Рассмотрим битовое представление чисел $$$a$$$, $$$b$$$, $$$x$$$. Посмотрим на какие-то $$$2$$$ бита на одинаковой позиции в $$$a$$$ и $$$b$$$, если они одинаковы, то независимо от того, что стоит в $$$x$$$, в числе $$$|({a \oplus x}) - ({b \oplus x})|$$$ на той же позиции будет стоять $$$0$$$. Поэтому на все такие позиции в $$$x$$$ выгодно поставить 0 (так как мы хотим, чтобы выполнялось $$$x \leq r$$$, а от бита ответ все равно не зависит). Если же биты в $$$a$$$ и $$$b$$$ на одной позиции отличаются, то на этой позиции будет $$$1$$$ либо в $$$a \oplus x$$$, либо в $$$b \oplus x$$$ в зависимости от того, что стоит на этой позиции в $$$x$$$.
Пусть $$$a$$$ < $$$b$$$, если нет, то поменяем их местами. Тогда на старшей позиции, из тех где биты различаются, в $$$a$$$ стоит $$$0$$$, а в $$$b$$$ стоит $$$1$$$. Есть $$$2$$$ варианта, либо поставить на эту позицию $$$1$$$ в $$$x$$$ (и тогда будет $$$1$$$ в $$$a \oplus x$$$), либо поставить $$$0$$$ в $$$x$$$ (и тогда будет $$$0$$$ в $$$a \oplus x$$$).
Пусть мы поставили $$$0$$$ в $$$x$$$, тогда $$$a \oplus x$$$ точно будет меньше, чем $$$b \oplus x$$$ (потому что в старшем различающемся бите $$$a \oplus x$$$ имеет $$$0$$$, а $$$b \oplus x$$$ имеет $$$1$$$). Поэтому на всех следующих позициях выгодно делать $$$1$$$ в $$$a \oplus x$$$, ведь так мы максимально приблизим эти числа, сделаем меньше их разность. Поэтому можно пойти по убыванию позиций, и если позиция различающаяся, то сделаем на этой позиции $$$1$$$ в $$$a \oplus x$$$, если это возможно (если при этом $$$x$$$ не превысит $$$r$$$).
Второй случай (когда мы поставили $$$1$$$ в $$$x$$$ на позицию первого различающегося бита) разбирается аналогично, но на самом деле он не нужен, ведь в нем ответ не станет меньше, а $$$x$$$ станет больше.
Асимптотика: $$$O(\log (10^{18}))$$$ на набор входных данных.
#include <bits/stdc++.h>
using namespace std;
const int maxb = 60;
bool get_bit(int64_t a,int i)
{
return a&(1ll<<i);
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--)
{
int64_t a,b,r;
cin >> a >> b >> r;
int64_t x = 0;
bool first_bit = 1;
if(a > b)
swap(a,b);
for(int i = maxb-1;i >= 0;--i)
{
bool bit_a = get_bit(a,i);
bool bit_b = get_bit(b,i);
if(bit_a != bit_b)
{
if(first_bit)
{
first_bit = 0;
}
else
{
if(!bit_a && x+(1ll<<i) <= r)
{
x += (1ll<<i);
a ^= (1ll<<i);
b ^= (1ll<<i);
}
}
}
}
cout << b-a << "\n";
}
}
Автор: ace5
Давайте сделаем бинарный поиск по ответу. Пусть мы знаем, что минимальная возможная стоимость не меньше $$$l$$$ и не больше $$$r$$$. Выберем $$$m = (l+r)/2$$$. Нам надо научиться проверять, что ответ меньше или равен $$$m$$$. Будем делать $$$dp_i$$$, это минимальная сумма заблокированных элементов на префиксе до $$$i$$$, если позиция $$$i$$$ заблокирована и на каждом из подотрезков без заблокированных сумма элементов меньше или равна $$$m$$$. Тогда $$$dp_i = a_i + \min(dp_j)$$$ по всем $$$j$$$, таким, что сумма на подотрезке от $$$j+1$$$ до $$$i-1$$$ меньше или равна $$$m$$$. Такие $$$j$$$ образуют отрезок, так как $$$a_j$$$ положительны. Будем поддерживать границы этого отрезка. Также будем поддерживать все $$$dp_j$$$ для $$$j$$$ внутри этого подотрезка в сете. При переходе от $$$i$$$ к $$$i+1$$$ нужно двигать левую границу подотрезка, пока сумма на нем не станет меньше или равна $$$m$$$, и удалять $$$dp_j$$$ из сета, а также добавлять в конец подотрезка $$$i$$$ и $$$dp_i$$$ в сет. Минимальную сумму заблокированных при условии, что на всех подотрезках без заблокированных сумма меньше или равна $$$m$$$, можно найти как минимум среди всех $$$dp_i$$$, таких что сумма от $$$i$$$ до $$$n$$$ меньше или равна $$$m$$$. Если этот ответ меньше или равен $$$m$$$, то и ответ на задачу меньше или равен $$$m$$$, иначе ответ больше $$$m$$$.
Асимптотика: $$$O(n \log n \log 10^9)$$$ на набор входных данных.
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
int64_t a[n+1];
for(int i = 0;i < n;++i)
{
cin >> a[i];
}
int64_t l = 0,r = int64_t(1e9)*n;
while(l < r)
{
int64_t m = (l+r)/2;
set<pair<int64_t,int>> pos;
int64_t dp[n+1];
int p2 = n;
dp[n] = 0;
pos.insert({dp[n],n});
int64_t sum = 0;
for(int j = n-1;j >= 0;--j)
{
while(sum > m)
{
sum -= a[p2-1];
pos.erase({dp[p2],p2});
p2--;
}
dp[j] = pos.begin()->first + a[j];
pos.insert({dp[j],j});
sum += a[j];
}
sum = 0;
int yes = 0;
for(int j =0;j < n;++j)
{
if(sum <= m && dp[j] <= m)
yes = 1;
sum += a[j];
}
if(yes)
r = m;
else
l = m+1;
}
cout << l << "\n";
}
}
Автор: ace5
Рандомизированное решение: Будем делать алгоритм быстрой сортировки (quicksort). Выберем рандомный элемент массива, пусть его индекс $$$i$$$, будем делать $$$?$$$ $$$i$$$, пока не получим ответ $$$=$$$ (то есть $$$x = a_i$$$). Теперь будем спрашивать про все остальные элементы, тем самым узнавая, больше они $$$a_i$$$ или меньше (надо не забывать возвращать $$$x = a_i$$$, то есть делать $$$?$$$ $$$i$$$ после каждого запроса про элемент), после этого разобьем все элементы на две части, где $$$a_i > x$$$ и $$$a_i < x$$$. В каждой части запустимся рекурсивно. Части будут становиться все меньше и меньше, в итоге мы отсортируем нашу перестановку, что позволит нам ее отгадать.
Нерандомизированное решение: Найдем элемент $$$1$$$ в массиве за $$$3n$$$ запросов. Для этого пройдемся по массиву, спрашивая каждый раз про очередной элемент. Если ответ $$$<$$$, то продолжим спрашивать, пока ответ не станет $$$=$$$, если ответ $$$=$$$ или $$$>$$$, перейдем к следующему. Тогда последний элемент, на котором был ответ $$$<$$$, и есть $$$1$$$. Число $$$x$$$ в процессе увеличится максимум на $$$n$$$ (от каждого элемента максимум по $$$1$$$), значит, уменьшится максимум на $$$2n$$$, то есть максимум $$$3n$$$ запросов. Аналогично найдем элемент $$$n$$$. Теперь запустим алгоритм аналогичный рандомизированному решению, только теперь мы можем сделать $$$x = n/2$$$, а не взять $$$x$$$ как рандомный элемент.
Оба решения с запасом укладываются в ограничение $$$40n$$$ запросов.
~~~~~
~~~~~
#include <bits/stdc++.h>
using namespace std;
char query(int pos)
{
cout << "? " << pos << endl;
char ans;
cin >> ans;
return ans;
}
void dnq(int l,int r,vector<int> pos,vector<int> & res,int pos1,int posn)
{
int m = (l+r)/2;
vector<int> lh;
vector<int> rh;
for(int i = 0;i < pos.size();++i)
{
char x = query(pos[i]);
if(x == '>')
{
rh.push_back(pos[i]);
query(pos1);
}
else if(x == '<')
{
lh.push_back(pos[i]);
query(posn);
}
else
{
res[pos[i]] = m;
}
}
if(lh.size() != 0)
{
int m2 = (l+m-1)/2;
for(int j = 0;j < m-m2;++j)
query(pos1);
dnq(l,m-1,lh,res,pos1,posn);
query(posn);
}
if(rh.size() != 0)
{
int m2 = (m+1+r)/2;
for(int j = 0;j < m2-m;++j)
query(posn);
dnq(m+1,r,rh,res,pos1,posn);
}
return ;
}
int main()
{
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
int pos1 = -1;
for(int i = 1;i <= n;++i)
{
char ans = query(i);
if(ans == '<')
{
i--;
}
else if(ans == '=')
{
pos1 = i;
}
else
{
if(pos1 != -1)
{
query(pos1);
}
}
}
int posn = -1;
for(int i = 1;i <= n;++i)
{
char ans = query(i);
if(ans == '>')
{
i--;
}
else if(ans == '=')
{
posn = i;
}
else
{
if(posn != -1)
{
query(posn);
}
}
}
vector<int> res(n+1);
vector<int> pos(n);
for(int j = 0;j < n;++j)
pos[j] = j+1;
int m = (1+n)/2;
for(int k = 0;k < n-m;++k)
{
query(pos1);
}
dnq(1,n,pos,res,pos1,posn);
cout << "! ";
for(int j = 1;j <= n;++j)
cout << res[j] << ' ';
cout << endl;
}
}
Автор: ooaa
Вначале можно заметить, что достаточно посетить все листья дерева. Ведь если гусеница пропустит какую-то внутреннюю вершину, то она никак не сможет попасть в поддерево этой вершины и посетить листья в нём. Поэтому нет смысла телепортироваться в корень не из листа (иначе было бы выгоднее переместиться в корень на ход раньше, и все листья остались бы посещёнными).
Оптимальный путь гусеницы по дереву можно разбить на перемещения из корня в лист, перемещения из одного листа в другой и телепортации из листа в корень. Пусть зафиксирован порядок посещения листьев в оптимальном пути. Тогда из последнего листа телепортироваться нет смысла, ведь все листья уже посещены. Кроме того, невыгодно двигаться не по кратчайшему пути на участках перехода из корня в лист без посещения других листьев, или перемещения из листа в лист без посещения других листьев. Если после листа $$$u$$$ посещается лист $$$v$$$, то телепортация из $$$u$$$ экономит время перехода из $$$u$$$ в $$$v$$$ минус время движения в $$$v$$$ из корня. Можно выбрать $$$k$$$ листьев, без последнего посещённого листа, которые дают максимальную экономию (если листьев в дереве меньше, или экономия становится отрицательной, то взять меньше $$$k$$$ листьев), и сделать телепортацию из них. Так, если известен порядок посещения листьев, можно найти оптимальное время.
Оказывается, что если взять дерево и отсортировать потомков каждой вершины по возрастанию (не убыванию) глубины поддерева, а потом выписать все листья слева направо (в порядке обхода в глубину), то это и будет один из оптимальных порядков листьев. Такой порядок сортировки дерева и листьев в нём будет называться порядком сортировки по глубине поддерева.
Можно отсортировать дерево таким образом одним обходом в глубину. Для каждого листа можно вычислить, сколько времени экономит телепортация из него. Для этого достаточно двигаться из этого листа к корню до первой развилки, для которой предыдущая вершина не самый правый потомок. Тогда экономия — длина пройденного пути минус оставшееся расстояние до корня. Такие пути для разных листьев не пересекаются по рёбрам, а оставшееся расстояние до корня можно преподсчитать в поиске в глубину сразу для всех. Поэтому алгоритм работает за время $$$O(n \log n)$$$, здесь логарифм появляется из-за сортировки потомков каждой вершины по глубине поддерева.
Теорема.
Существует кратчайший маршрут гусеницы, в котором листья посещаются в порядке сортировки потомков каждой вершины по глубине поддерева.
Пусть $$$u_1, \ldots, u_m$$$ — все листья дерева по порядку, который получится, если отсортировать потомков каждой вершины по возрастанию глубины поддерева. Рассматривается кратчайший маршрут гусеницы, посещающий все вершины дерева. Пусть $$$v_1, \ldots, v_m$$$ — листья дерева, в порядке посещения в этом маршруте. Рассматривается максимальный префикс листьев, совпадающий с порядком сортировки по глубине поддерева: $$$v_1 = u_1,\ldots, v_i = u_i$$$. Если $$$i = m$$$, то теорема доказана. Теперь пусть дальше идёт неправильный лист $$$v_{i+1} \neq u_{i+1}$$$.
Цель — так изменить маршрут, чтобы время обхода дерева не увеличилось, чтобы первые $$$i$$$ посещённых листьев не изменились и остались в том же порядке, и чтобы лист $$$u_{i+1}$$$ встретился в маршруте раньше, чем до изменения. Тогда так можно двигать лист $$$u_{i+1}$$$ к началу маршрута, пока он не встанет на своё $$$(i+1)$$$-е место. Дальше таким же образом по очереди поставить на свои места все листья $$$u_{i+1}, \ldots, u_m$$$ и получить кратчайший маршрут гусеницы с желаемым порядком посещения листьев.
Вначале доказывается лемма.
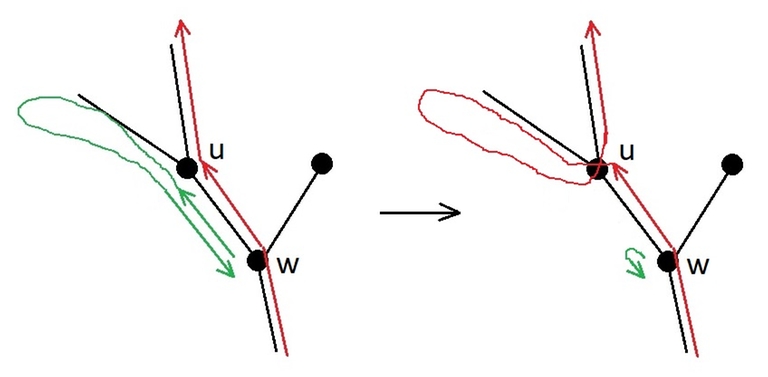
Лемма.
Пусть вершина $$$w$$$ — предок вершины $$$u$$$. Пусть гусеница в кратчайшем маршруте по дереву переползает из $$$u$$$ в $$$w$$$. Тогда гусеница заходит в поддерево вершины $$$u$$$ только один раз, обходит это поддерево в глубину, и возвращается в $$$w$$$.
Доказательство леммы.
Если гусеница ползёт из $$$w$$$ в $$$u$$$ только один раз, то нельзя покидать поддерево $$$u$$$, пока не будут посещены все вершины, и нельзя прыгать на батут, так как надо ещё переместиться из $$$u$$$ в $$$w$$$. Всё это нельзя сделать быстрее, чем за число шагов, равное удвоенному числу вершин в поддереве $$$u$$$, ведь в каждую вершину нужно прийти по ребру из предка и вернуться в предка. А любой маршрут без телепортаций, который использует каждое ребро по два раза, — это один из обходов в глубину.
Если гусеница ползёт из $$$w$$$ в $$$u$$$ два и более раз, то маршрут можно сократить, как на рисунке.
Лемма доказана.
В данный момент лист $$$v_{i+1}$$$ находится в порядке посещения листьев оптимальным маршрутом гусеницы на месте листа $$$u_{i+1}$$$. Цель: суметь подвинуть лист $$$u_{i+1}$$$ поближе к началу маршрута, не меняя первые $$$i$$$ листьев: $$$u_1, \ldots, u_i$$$.
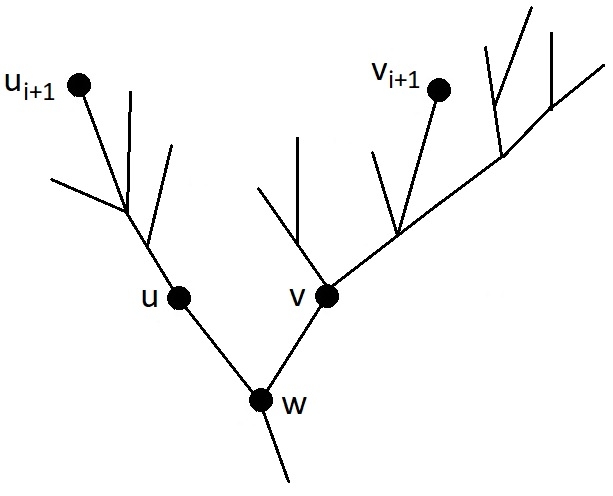
Пусть $$$w$$$ — наименьший общий предок листьев $$$u_{i+1}$$$ и $$$v_{i+1}$$$, пусть $$$u$$$ — потомок $$$w$$$, в поддереве которого находится вершина $$$u_{i+1}$$$, а $$$v$$$ — потомок $$$w$$$, в поддереве которого лежит $$$v_{i+1}$$$, как на рисунке. Чтобы немного подвинуть лист $$$u_{i+1}$$$ к началу маршрута, надо разобрать случаи.
Случай 1: Гусеница в текущем варианте оптимального маршрута переползает из $$$u$$$ в $$$w$$$.
В этом случае, по лемме гусеница заходит в поддерево вершины $$$u$$$ только один раз, и обходит его в глубину, прежде, чем вернуться в $$$w$$$. В поддереве вершины $$$u$$$ нет листьев $$$u_1, \ldots, u_i$$$, потому что все листья поддерева $$$u$$$ посещаются подряд в процессе обхода в глубину, а лист $$$v_{i+1}$$$ не из поддерева $$$u$$$ посещается после $$$u_1, \ldots, u_i$$$, но до $$$u_{i+1}$$$. Тогда маршрут можно изменить так: цикл $$$w \to \text{ (обход поддерева } u\text{) } \to w$$$ вырезается из того места, где он находится, и вставляется в момент первого посещения $$$w$$$ после посещения листа $$$u_i$$$. Лист $$$u_i$$$ не лежит в поддереве вершины $$$v$$$, потому что поддерево $$$u$$$ имеет меньшую глубину ($$$u_{i+1}$$$ раньше в желаемом порядке листьев, чем $$$v_{i+1}$$$), и в нём ещё остались не посещённые листья. Тогда, прежде, чем зайти в $$$v_{i+1}$$$, гусенице придётся прийти из листа $$$u_i$$$ в вершину $$$w$$$, и в этот момент произойдёт обход в глубину поддерева $$$u$$$ с посещением листа $$$u_{i+1}$$$. Этот обход был перенесён на более раннее время, до посещения $$$v_{i+1}$$$, значит, в порядке посещения листьев в маршруте гусеницы лист $$$u_{i+1}$$$ продвинулся к началу.
Случай 2: Гусеница в текущем варианте оптимального маршрута не ползёт из $$$u$$$ в $$$w$$$, но переползает из $$$v$$$ в $$$w$$$.
Тогда всё поддерево $$$v$$$ обходится обходом в глубину. Так как лист $$$u_{i+1}$$$ лежит в желаемом порядке раньше, чем $$$v_{i+1}$$$, то поддерево $$$v$$$ более глубокое, чем поддерево $$$u$$$, и в желаемом порядке все листья $$$v$$$ идут позже $$$u_{i+1}$$$. Кроме того, поскольку гусеница не ползёт из $$$u$$$ в $$$w$$$, из поддерева $$$u$$$ не выбраться иначе как телепортацией в корень. Рассматривается последний прыжок на батут (или остановка в конце маршрута) из поддерева вершины $$$u$$$. В этот момент посещены все листья поддерева $$$u$$$. Маршрут можно изменить так: вырезать обход в глубину поддерева $$$v$$$, отменить последний прыжок или остановку в поддереве $$$u$$$, оттуда спуститься в $$$w$$$, выполнить обход поддерева $$$v$$$ в глубину так, чтобы последней посетить самую глубокую вершину этого поддерева, и из неё телепортироваться в корень (или остановиться в конце маршрута). Это будет не длиннее, потому что добавился участок перехода из листа в поддереве $$$u$$$ в $$$w$$$, а исчез участок перемещения из самого глубокого листа в поддереве $$$v$$$ в $$$w$$$, здесь важно, что поддерево $$$v$$$ глубже, чем поддерево $$$u$$$. И вершина $$$u_{i+1}$$$ стала ближе к началу списка посещения листьев, потому что все листья поддерева $$$v$$$, включая $$$v_{i+1}$$$, переместились куда-то после всех листьев поддерева $$$u$$$.
Случай 3: Гусеница в текущем варианте оптимального маршрута не переползает как из $$$u$$$ в $$$w$$$, так и из $$$v$$$ в $$$w$$$.
Тогда все участки маршрута, попадающие в поддеревья вершин $$$u$$$ и $$$v$$$, не покидают эти поддеревья и заканчиваются телепортацией в корень или остановкой в конце маршрута. Среди них есть участок, начинающийся с шага из $$$w$$$ в $$$u$$$, в котором посещается лист $$$u_{i+1}$$$, и участок, начинающийся с шага из $$$w$$$ в $$$v$$$, в котором посещается лист $$$v_{i+1}$$$. В текущем маршруте участок с $$$v_{i+1}$$$ идёт раньше. Изменение маршрута очень простое: поменять местами участок, посещающий лист $$$u_{i+1}$$$, и участок, посещающий лист $$$v_{i+1}$$$. Если оба заканчиваются телепортациями, то получится корректный маршрут гусеницы. Если гусеница останавливалась в конце участка, посещающего $$$u_{i+1}$$$, и телепортировалась в корень из участка с $$$v_{i+1}$$$, то теперь она будет телепортироваться после завершения участка с $$$u_{i+1}$$$ и останавливаться в конце участка с $$$v_{i+1}$$$. Положение листьев $$$u_1, \ldots, u_i$$$ в маршруте не изменится: их нет в поддереве $$$v$$$, и их нет в участке с $$$u_{i+1}$$$, посещавшемся после $$$v_{i+1}$$$. И лист $$$u_{i+1}$$$ получит более близкое к началу место в порядке посещения листьев, потому что участок с его посещением теперь встречается в маршруте раньше.
Во всех случаях удалось подвинуть лист $$$u_{i+1}$$$ в оптимальном маршруте гусеницы поближе к началу, сохраняя первые $$$i$$$ листьев, значит, существует оптимальный маршрут гусеницы, в котором листья посещаются в порядке сортировки поддеревьев дерева по глубине. Теорема доказана.
#include <bits/stdc++.h>
using namespace std;
const int maxn = 200005;
int d[maxn];
int h[maxn];
int p[maxn];
vector<int> leaf_jump_gains;
vector<vector<int> > children;
bool comp_by_depth(int u,int v)
{
return d[u] < d[v];
}
void sort_subtrees_by_depth(int v)
{
d[v] = 0;
if(v == 1)
h[v] = 0;
else
h[v] = h[p[v]]+1;
for(int i = 0; i < int(children[v].size()); ++i)
{
int u = children[v][i];
sort_subtrees_by_depth(u);
d[v] = max(d[v],d[u]+1);
}
sort(children[v].begin(),children[v].end(),comp_by_depth);
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int n,k;
cin >> n >> k;
children.resize(n+1);
for(int i = 2; i <= n; ++i)
{
cin >> p[i];
children[p[i]].push_back(i);
}
sort_subtrees_by_depth(1);
for(int i = 1; i <= n; ++i)
{
if(children[i].size() == 0)
{
int jump_gain = 0;
int v = i;
while(v != 1)
{
int s = children[p[v]].size();
if(children[p[v]][s-1] == v)
{
v = p[v];
++jump_gain;
}
else
{
jump_gain = jump_gain+1-h[p[v]];
break;
}
}
leaf_jump_gains.push_back(jump_gain);
}
}
sort(leaf_jump_gains.begin(),leaf_jump_gains.end());
int s = leaf_jump_gains.size();
++k; //non-returning from the last leaf is like one more jump
int res = 2*(n-1);
for(int i = s-1; i >= max(0,s-k); --i)
res -= max(leaf_jump_gains[i],0);
cout << res << '\n';
return 0;
}
1918G — Перестановка от исходного
Автор: ace5
Вначале можно вручную подобрать ответы для маленьких значений $$$n$$$. Для $$$n = 2,4,6$$$ получится ответ "YES" и массивы $$$[-1,1], [-1,-2,2,1], [-1,-2,2,1,-1,1]$$$. Несложно доказать разбором случаев, что для $$$3$$$ и $$$5$$$ ответ "NO". Можно предположить, что для всех нечётных $$$n$$$ ответ "NO", но если попробовать доказать отсутствие массива или подобрать массив для $$$n = 7$$$, окажется, что массив существует: $$$[-5, 8, 1, -3, -4,-2, 5]$$$. На самом деле, массив существует для всех $$$n$$$, кроме $$$3$$$ и $$$5$$$.
Было бы просто, если бы можно было сделать, чтобы число в каждой ячейке не менялось. Но наличие краёв массива и запрет на нули делают это невозможным. Дальше, можно заметить, что бесконечный массив, в котором повторяется шестёрка чисел $$$1, -3, -4, -1, 3, 4$$$, порождает в каждой ячейке то же число, которое там было. Вообще таким свойством будет обладать любая шестёрка чисел вида $$$a,-b,-a-b,-a,b,a+b$$$. Так можно переводить внутренние ячейки массива в ячейки с такими же числами, вопрос в том, что делать на краях. В авторском решении были вручную подобраны подходящие края (возможно, из нескольких чисел) для каждого остатка от деления на $$$6$$$. А дальше решение для каждого значения $$$n$$$ создавалось так: взять края для $$$n \mod 6$$$ и вставить в середину столько шестёрок чисел, переходящих в себя, сколько потребуется.
Решение green_gold_dog:
Идея в том, что любой правильный массив можно увеличить на $$$2$$$ элемента, чтобы массив остался правильным. Пусть массив заканчивается на числа $$$a$$$ и $$$b$$$. Тогда его можно увеличить на два элемента так: \begin{equation*} [\ldots,\;a,\;b] \to [\ldots, a,\; b,\; -b,\; a-b] \end{equation*} Этот массив переходит в свою перестановку: весь старый массив, кроме $$$a$$$, порождается старым массивом; в последних трёх ячейках порождаются $$$a-b$$$, $$$a$$$, $$$-b$$$, то есть два новых элемента, и пропавший элемент $$$a$$$. Ещё нужно, чтобы новые элементы были не нулями. Если последние два элемента старого массива были разными, то новые элементы не нули, кроме того, новые элементы не могут оказаться одинаковыми, так как $$$a$$$ и $$$b$$$ не нули, поэтому эту операцию можно повторять много раз.
Чтобы стартовать, достаточно два массива: $$$[1,2]$$$ для $$$n = 2$$$ и $$$[1,2,-3,2,4,-5,-2]$$$ для $$$n = 7$$$. Дальше можно удлинять эти массивы на $$$2$$$, чтобы получить ответ для чётного или нечётного $$$n$$$.
Оба решения печатают массив по простым правилам и работают за $$$O(n)$$$ времени.
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int n;
cin >> n;
if(n%6 == 0)
{
cout << "YES\n";
cout << "2 1 -1 ";
for(int j = 0;j < n/6-1;++j)
{
cout << "1 -1 -2 -1 1 2 ";
}
cout << "1 -1 -2" << "\n";
return 0;
}
else if(n%6 == 1)
{
cout << "YES\n";
cout << "-5 8 1 -3 -4 ";
for(int j = 0;j < n/6-1;++j)
{
cout << "-1 3 4 1 -3 -4 ";
}
cout << "-2 5" << "\n";
return 0;
}
else if(n%6 == 2)
{
cout << "YES\n";
for(int j = 0;j < n/6;++j)
{
cout << "1 -1 -2 -1 1 2 ";
}
cout << "1 -1" << "\n";
return 0;
}
else if(n%6 == 3)
{
if(n == 3)
cout << "NO\n";
else
{
cout << "YES\n";
cout << "2 1 1 -3 -4 -1 3 ";
for(int j = 0;j < n/6-1;++j)
{
cout << "4 1 -3 -4 -1 3 ";
}
cout << "3 -2" << "\n";
return 0;
}
}
else if(n%6 == 4)
{
cout << "YES\n";
for(int j = 0;j < n/6;++j)
{
cout << "1 -1 -2 -1 1 2 ";
}
cout << "1 -1 1 2" << "\n";
return 0;
}
else if(n%6 == 5)
{
if(n == 5)
{
cout << "NO\n";
}
else
{
cout << "YES\n";
cout << "-2 1 1 -3 -4 -1 3 ";
for(int j = 0;j < n/6-1;++j)
{
cout << "4 1 -3 -4 -1 3 ";
}
cout << "2 -1 2 4" << "\n";
return 0;
}
}
}
//#pragma GCC optimize("Ofast")
//#pragma GCC target("avx,avx2,sse,sse2,sse3,ssse3,sse4,abm,popcnt,mmx")
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
typedef long double ldb;
typedef complex<double> cd;
constexpr ll INF64 = 9'000'000'000'000'000'000, INF32 = 2'000'000'000, MOD = 1'000'000'007;
constexpr db PI = acos(-1);
constexpr bool IS_FILE = false, IS_TEST_CASES = false;
random_device rd;
mt19937 rnd32(rd());
mt19937_64 rnd64(rd());
template<typename T>
bool assign_max(T& a, T b) {
if (b > a) {
a = b;
return true;
}
return false;
}
template<typename T>
bool assign_min(T& a, T b) {
if (b < a) {
a = b;
return true;
}
return false;
}
template<typename T>
T square(T a) {
return a * a;
}
template<>
struct std::hash<pair<ll, ll>> {
ll operator() (pair<ll, ll> p) const {
return ((__int128)p.first * MOD + p.second) % INF64;
}
};
void solve() {
ll n;
cin >> n;
if (n == 5 || n == 3) {
cout << "NO\n";
return;
}
cout << "YES\n";
vector<ll> arr;
if (n % 2 == 0) {
arr.push_back(1);
arr.push_back(2);
} else {
arr.push_back(1);
arr.push_back(2);
arr.push_back(-3);
arr.push_back(2);
arr.push_back(4);
arr.push_back(-5);
arr.push_back(-2);
}
while (arr.size() != n) {
ll x = arr[arr.size() - 2];
ll y = x - arr.back();
ll z = y - x;
arr.push_back(z);
arr.push_back(y);
}
for (auto i : arr) {
cout << i << ' ';
}
cout << '\n';
}
int main() {
if (IS_FILE) {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
ll t = 1;
if (IS_TEST_CASES) {
cin >> t;
}
for (ll i = 0; i < t; i++) {
solve();
}
}






